如图,在正方形ABCD中,AB=3,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF.
(1)依题意补全图1;
(2)若DM=1,求线段EF的长;
(3)当点M在CD边上运动时,能使△AEF为等腰三角形,直接写出此时tan∠DAM的值.
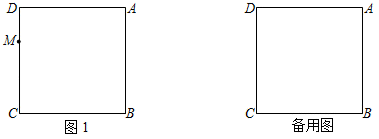
(1)依题意补全图1;
(2)若DM=1,求线段EF的长;
(3)当点M在CD边上运动时,能使△AEF为等腰三角形,直接写出此时tan∠DAM的值.

更新时间:2020/06/02 15:10:34
|
相似题推荐
解答题-证明题
|
较难
(0.4)
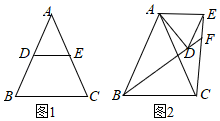
【推荐1】如图,在△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D.
(1)求证: BE=CF;
(2)请探究旋转角等于多少度时,四边形ABDF为菱形,证明你的结论;
(3)在(2)的条件下,求CD的长.

(1)求证: BE=CF;
(2)请探究旋转角等于多少度时,四边形ABDF为菱形,证明你的结论;
(3)在(2)的条件下,求CD的长.

您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
【推荐2】如图1,在 ABC中,AB=AC,点D,E分别在边AB,AC上,且AD=AE,连接DE,现将
ABC中,AB=AC,点D,E分别在边AB,AC上,且AD=AE,连接DE,现将 ADE绕点A逆时针旋转一定角度(如图2),连接BD,CE.
ADE绕点A逆时针旋转一定角度(如图2),连接BD,CE.
(1)求证: ABD≌
ABD≌ ACE;
ACE;
(2)延长BD交CE于点F,若AD⊥BD,BD=6,CF=4,求线段DF的长.
 ABC中,AB=AC,点D,E分别在边AB,AC上,且AD=AE,连接DE,现将
ABC中,AB=AC,点D,E分别在边AB,AC上,且AD=AE,连接DE,现将 ADE绕点A逆时针旋转一定角度(如图2),连接BD,CE.
ADE绕点A逆时针旋转一定角度(如图2),连接BD,CE.(1)求证:
 ABD≌
ABD≌ ACE;
ACE;(2)延长BD交CE于点F,若AD⊥BD,BD=6,CF=4,求线段DF的长.

您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
【推荐1】在 中,AD是角平分线.
中,AD是角平分线. ,
,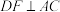 .已知
.已知 ,
,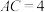 ,
,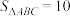 ,求
,求 的长;
的长;
(2)如图2,求证: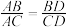 ;
;
(3)如图3, ,
, ,
, .若
.若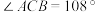 ,求证:
,求证: .
.
 中,AD是角平分线.
中,AD是角平分线.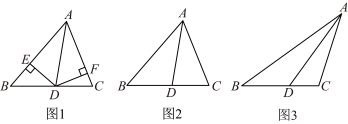
 ,
,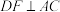 .已知
.已知 ,
,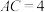 ,
, ,求
,求 的长;
的长;(2)如图2,求证:
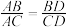 ;
;(3)如图3,
 ,
, ,
, .若
.若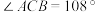 ,求证:
,求证: .
.
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
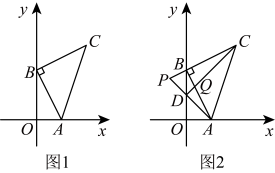
【推荐2】如图1,在直角坐标系中,点 在第一象限,且
在第一象限,且 为等腰直角三角形,
为等腰直角三角形, ,已知点
,已知点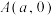 ,点
,点 ,且
,且 ,
, 满足
满足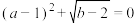 .
.
(1) ______,
______, ______;
______;
(2)求点 的坐标;
的坐标;
(3)如图2,点 在
在 轴上,且
轴上,且 ,连接
,连接 与
与 相交于点
相交于点 ,延长
,延长 与
与 相交于点
相交于点 ,判断
,判断 与
与 的位置与数量关系,并证明.
的位置与数量关系,并证明.
 在第一象限,且
在第一象限,且 为等腰直角三角形,
为等腰直角三角形, ,已知点
,已知点 ,点
,点 ,且
,且 ,
, 满足
满足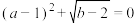 .
.
(1)
 ______,
______, ______;
______;(2)求点
 的坐标;
的坐标;(3)如图2,点
 在
在 轴上,且
轴上,且 ,连接
,连接 与
与 相交于点
相交于点 ,延长
,延长 与
与 相交于点
相交于点 ,判断
,判断 与
与 的位置与数量关系,并证明.
的位置与数量关系,并证明.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐1】如图,矩形ABCD中,AB=4cm,AD=5cm,E是AD上一点,DE=3cm,连接BE、CE.点P从点C出发,沿CE方向向点E匀速运动,运动速度2cm/s,同时点Q从点B出发,沿BC方向匀速运动,运动速度均为1cm/s,连接PQ. 设点P、Q的运动时间为t(s)(0<t<2.5).
(1)当t为何值时,△PQC是等腰三角形?
(2)设五边形ABQPE的面积为 (cm2),求
(cm2),求 与t之间的函数关系式.
与t之间的函数关系式.
(3)是否存在某一时刻t,使得S五边形ABQPE∶S矩形ABCD=23∶50?若存在,求出t的值,并求出此时PQ的长;若不存在,请说明理由.
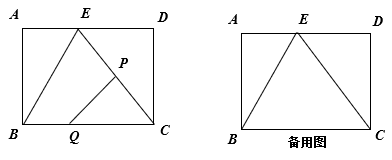
(1)当t为何值时,△PQC是等腰三角形?
(2)设五边形ABQPE的面积为
 (cm2),求
(cm2),求 与t之间的函数关系式.
与t之间的函数关系式.(3)是否存在某一时刻t,使得S五边形ABQPE∶S矩形ABCD=23∶50?若存在,求出t的值,并求出此时PQ的长;若不存在,请说明理由.

您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
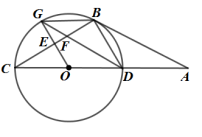
名校
【推荐2】已知 ,
, 为
为 的直径,连结
的直径,连结 ,
, ,点
,点 是
是 上一点,且
上一点,且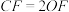 .
.
(1)如图,若 ,
,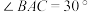 ,求
,求 的长;
的长;

(2)若 ,点
,点 是
是 上一点,连结
上一点,连结 ,交
,交 于点
于点 ;
;
①如图,当点 为
为 中点时,求
中点时,求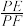 的值;
的值;

②连结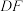 ,当
,当 时,
时,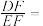 ___________;
___________;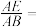 ___________(利用备用图探索)
___________(利用备用图探索)
 ,
, 为
为 的直径,连结
的直径,连结 ,
, ,点
,点 是
是 上一点,且
上一点,且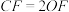 .
.(1)如图,若
 ,
,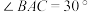 ,求
,求 的长;
的长;
(2)若
 ,点
,点 是
是 上一点,连结
上一点,连结 ,交
,交 于点
于点 ;
;①如图,当点
 为
为 中点时,求
中点时,求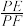 的值;
的值;
②连结
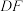 ,当
,当 时,
时,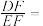 ___________;
___________;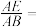 ___________(利用备用图探索)
___________(利用备用图探索)
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
【推荐3】学习了《中心对称图形》后,阿中与茜茜对平行四边形进行了再次探究: ,其中
,其中 ,在
,在 边上取一点D(不是中点),连接
边上取一点D(不是中点),连接 ,沿
,沿 剪开纸片,重新拼接……”,
剪开纸片,重新拼接……”,
请你完成茜茜的举反例过程,画出相应的图形,并配以必要的说明;
(2)阿中进一步探究发现:“一组对边相等且一组对角是直角的四边形是矩形”,请你完成证明过程;
已知:如图2,四边形 中,
中, ,
,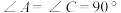 ,求证:四边形
,求证:四边形 是矩形.
是矩形.
(3)茜茜发现折叠矩形可以得到菱形:如图3,将矩形 折叠,使得A、C两点重合,点B落在点
折叠,使得A、C两点重合,点B落在点 ,折痕分别交边
,折痕分别交边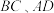 于E、F两点,交
于E、F两点,交 于O两点,则四边形
于O两点,则四边形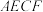 是菱形.请在框图中补全茜茜的证明思路.
是菱形.请在框图中补全茜茜的证明思路.
茜茜的证明思路
(4)茜茜给阿中出了一道思考题:“如图4,在矩形 中,
中, ,
, ,点E、F分别是边
,点E、F分别是边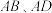 上的点,将矩形
上的点,将矩形 沿着直线
沿着直线 折叠,使点A与矩形
折叠,使点A与矩形 内部的点P重合,问
内部的点P重合,问 的最小值是多少?”请聪明的你用矩形纸片操作探究一下,直接写出
的最小值是多少?”请聪明的你用矩形纸片操作探究一下,直接写出 的最小值.
的最小值.
 ,其中
,其中 ,在
,在 边上取一点D(不是中点),连接
边上取一点D(不是中点),连接 ,沿
,沿 剪开纸片,重新拼接……”,
剪开纸片,重新拼接……”,请你完成茜茜的举反例过程,画出相应的图形,并配以必要的说明;
(2)阿中进一步探究发现:“一组对边相等且一组对角是直角的四边形是矩形”,请你完成证明过程;
已知:如图2,四边形
 中,
中, ,
, ,求证:四边形
,求证:四边形 是矩形.
是矩形.(3)茜茜发现折叠矩形可以得到菱形:如图3,将矩形
 折叠,使得A、C两点重合,点B落在点
折叠,使得A、C两点重合,点B落在点 ,折痕分别交边
,折痕分别交边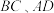 于E、F两点,交
于E、F两点,交 于O两点,则四边形
于O两点,则四边形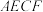 是菱形.请在框图中补全茜茜的证明思路.
是菱形.请在框图中补全茜茜的证明思路.茜茜的证明思路
由折叠易知 是 是 的垂直平分线,可以先证 的垂直平分线,可以先证 ① ,得到② ,又由 ① ,得到② ,又由 ,可得四边形 ,可得四边形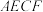 是平行四边形,再由③ ,于是 是平行四边形,再由③ ,于是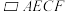 是菱形. 是菱形. |
(4)茜茜给阿中出了一道思考题:“如图4,在矩形
 中,
中, ,
, ,点E、F分别是边
,点E、F分别是边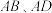 上的点,将矩形
上的点,将矩形 沿着直线
沿着直线 折叠,使点A与矩形
折叠,使点A与矩形 内部的点P重合,问
内部的点P重合,问 的最小值是多少?”请聪明的你用矩形纸片操作探究一下,直接写出
的最小值是多少?”请聪明的你用矩形纸片操作探究一下,直接写出 的最小值.
的最小值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
真题
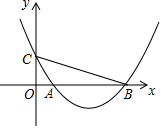
【推荐1】如图,在平面直角坐标系 中,二次函数图象的顶点坐标为
中,二次函数图象的顶点坐标为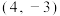 ,该图象与
,该图象与 轴相交于点
轴相交于点 、
、 ,与
,与 轴相交于点
轴相交于点 ,其中点
,其中点 的横坐标为1.
的横坐标为1.
(1)求该二次函数的表达式;
(2)求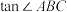 .
.
 中,二次函数图象的顶点坐标为
中,二次函数图象的顶点坐标为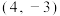 ,该图象与
,该图象与 轴相交于点
轴相交于点 、
、 ,与
,与 轴相交于点
轴相交于点 ,其中点
,其中点 的横坐标为1.
的横坐标为1.
(1)求该二次函数的表达式;
(2)求
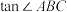 .
.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐2】如图,

(1)尝试探究
如图1,在△ABC中,∠ACB=90°,∠A=60°,E、F分别是边AC、BC上的点,且EF∥AB.
①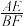 的值为______;②直线AE与直线BF的位置关系为______.
的值为______;②直线AE与直线BF的位置关系为______.
(2)类比延伸
如图2,若将图1中的△CEF绕点C逆时针旋转,旋转角小于90°,连接AE,BF,则在旋转的过程中,请判断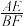 的值及直线AE与直线BF的位置关系,并说明理由.
的值及直线AE与直线BF的位置关系,并说明理由.
(3)拓展运用
如图3,在四边形ABCD中,在连接AC,BD,AC⊥BC,∠CAB=∠ADC=60°,AD=4,求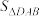 .
.

(1)尝试探究
如图1,在△ABC中,∠ACB=90°,∠A=60°,E、F分别是边AC、BC上的点,且EF∥AB.
①
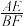 的值为______;②直线AE与直线BF的位置关系为______.
的值为______;②直线AE与直线BF的位置关系为______.(2)类比延伸
如图2,若将图1中的△CEF绕点C逆时针旋转,旋转角小于90°,连接AE,BF,则在旋转的过程中,请判断
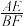 的值及直线AE与直线BF的位置关系,并说明理由.
的值及直线AE与直线BF的位置关系,并说明理由.(3)拓展运用
如图3,在四边形ABCD中,在连接AC,BD,AC⊥BC,∠CAB=∠ADC=60°,AD=4,求
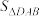 .
.
您最近一年使用:0次

 线段FD与线段FC的关系并证明;
线段FD与线段FC的关系并证明; ,写出你的结论并证明;
,写出你的结论并证明; ,直接写出线段BF的范围.
,直接写出线段BF的范围.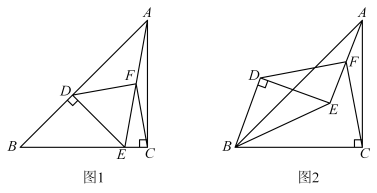
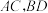 的交点,
的交点, 平分
平分 ,交
,交 于点H,分别交
于点H,分别交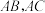 于点E,G.
于点E,G.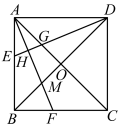
 ;
;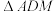 是等腰三角形吗?请说明理由;
是等腰三角形吗?请说明理由;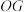 的长为1,求BE的长度.
的长为1,求BE的长度.
 作
作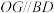 交
交 ,交
,交 交
交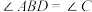 时,求证:
时,求证: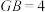 ,
,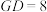 ,求
,求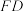 的长;
的长;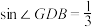 ,求
,求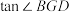 的值.
的值.