如图 ,有一块三角形菜地,若从顶点
,有一块三角形菜地,若从顶点 修一条小路交
修一条小路交 于点
于点 ,小路正好将菜地分成面积相等的两部分.
,小路正好将菜地分成面积相等的两部分. 点的位置并说明理由.
点的位置并说明理由.
(2)假设在菜地中有一点 (如图
(如图 所示),
所示), 上是否存在点
上是否存在点 ,使折线
,使折线 将三角形
将三角形 的面积分为面积相等的两部分.若存在,请画出
的面积分为面积相等的两部分.若存在,请画出 点的位置.
点的位置.
 ,有一块三角形菜地,若从顶点
,有一块三角形菜地,若从顶点 修一条小路交
修一条小路交 于点
于点 ,小路正好将菜地分成面积相等的两部分.
,小路正好将菜地分成面积相等的两部分.
 点的位置并说明理由.
点的位置并说明理由.(2)假设在菜地中有一点
 (如图
(如图 所示),
所示), 上是否存在点
上是否存在点 ,使折线
,使折线 将三角形
将三角形 的面积分为面积相等的两部分.若存在,请画出
的面积分为面积相等的两部分.若存在,请画出 点的位置.
点的位置.
21-22七年级下·上海杨浦·期中 查看更多[5]
上海外国语大学附属双语学校2021-2022学年七年级下学期期中数学试卷 上海市上海外国语大学附属双语学校2021-2022学年七年级下学期线上期中阶段练习数学试卷(已下线)核心考点03 三角形有关概念与性质-【满分全攻略】2022-2023学年七年级数学下学期核心考点+重难点讲练与测试(沪教版)2023年江苏省扬州市邗江区梅岭中学中考数学适应性试题(三)江苏省无锡市江阴市南闸实验学校2023-2024学年九年级下学期3月月考数学试题
更新时间:2022/09/20 22:04:47
|
相似题推荐
解答题-证明题
|
适中
(0.65)
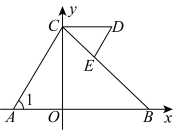
【推荐1】如图,平面直角坐标系中,C(0,5)、D(a,5)(a>0),A、B在x轴上,∠1=∠D,请写出∠ACB和∠BED数量关系以及证明.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
【推荐2】(1)仔细读题,完成下列说理填空,
已知:如图, ,直线
,直线 交
交 于点
于点 ,
, .
.
求证: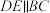 .
. (______),
(______),
所以 (______).
(______).
因为 (已知),
(已知),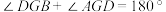 ;
;
所以______(等量代换).
所以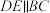 (______).
(______).
(2)聪明的你,请写出一种与第(1)题不同的证明方法(格式仿照第(1)小题证明过程,不用写理由).
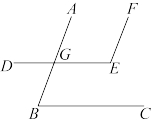
已知:如图,
 ,直线
,直线 交
交 于点
于点 ,
, .
.求证:
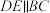 .
.
 (______),
(______),所以
 (______).
(______).因为
 (已知),
(已知),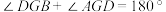 ;
;所以______(等量代换).
所以
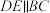 (______).
(______).(2)聪明的你,请写出一种与第(1)题不同的证明方法(格式仿照第(1)小题证明过程,不用写理由).
您最近一年使用:0次
解答题-作图题
|
适中
(0.65)
名校
【推荐1】小小设计师——探究面积等分问题
问题提出:
物业公司计划绿化一块不规则空地,要求使用一条直线将空地分为面积相等的两部分,一部分种花,另一部分种植绿色植被.若你是设计师,应怎样设计才能满足要求?
探索化归:
若一条直线把一个平面图形分为面积栩等的两部分,那么我们把这条直线称为这个平面图形的一条面积等分线.
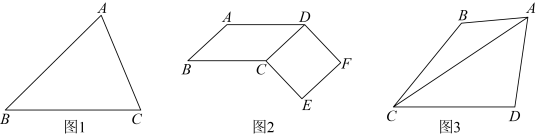
(1)小明从最简单的图形——三角形入手,很快就想到了它的一条面积等分线.如图1.过点A,利用尺规作出一条 的面积等分线(保留作网痕迹,不写作法);
的面积等分线(保留作网痕迹,不写作法);
(2)平行四边形是中心对称图形,过对称中心的直线可以将其分成面积相等的两部分.图2由一个平行四边形和一个正方形组成,请仅用无刻度直尺画出这个图形的一条面积等分线(保留作图痕迹,不写画法);
问题解决:
(3)在等分图形面积的过程中,小明发现了如下结论:
如图,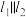 ,点
,点 ,
, ,
, 在
在 上,点
上,点 ,
, 在
在 上,则
上,则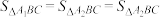 .
.
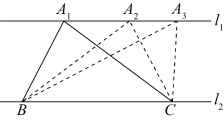
如图3,四边形 中,
中, 与
与 不平行,
不平行,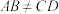 ,且
,且 ,请在图3中,过点
,请在图3中,过点 画出四边形
画出四边形 的一条面积等分线,写出画法,并说明理由.
的一条面积等分线,写出画法,并说明理由.
问题提出:
物业公司计划绿化一块不规则空地,要求使用一条直线将空地分为面积相等的两部分,一部分种花,另一部分种植绿色植被.若你是设计师,应怎样设计才能满足要求?
探索化归:
若一条直线把一个平面图形分为面积栩等的两部分,那么我们把这条直线称为这个平面图形的一条面积等分线.

(1)小明从最简单的图形——三角形入手,很快就想到了它的一条面积等分线.如图1.过点A,利用尺规作出一条
 的面积等分线(保留作网痕迹,不写作法);
的面积等分线(保留作网痕迹,不写作法);(2)平行四边形是中心对称图形,过对称中心的直线可以将其分成面积相等的两部分.图2由一个平行四边形和一个正方形组成,请仅用无刻度直尺画出这个图形的一条面积等分线(保留作图痕迹,不写画法);
问题解决:
(3)在等分图形面积的过程中,小明发现了如下结论:
如图,
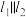 ,点
,点 ,
, ,
, 在
在 上,点
上,点 ,
, 在
在 上,则
上,则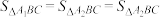 .
.
如图3,四边形
 中,
中, 与
与 不平行,
不平行,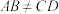 ,且
,且 ,请在图3中,过点
,请在图3中,过点 画出四边形
画出四边形 的一条面积等分线,写出画法,并说明理由.
的一条面积等分线,写出画法,并说明理由.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
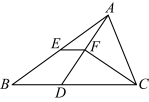
【推荐2】如图,在 中,
中, ,点D在
,点D在 上,且
上,且 ,
,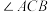 的平分线
的平分线 交
交 于F,点E是
于F,点E是 的中点,连接
的中点,连接 .
.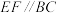 ;
;
(2)若四边形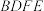 的面积为6,求
的面积为6,求 的面积.
的面积.
 中,
中, ,点D在
,点D在 上,且
上,且 ,
,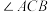 的平分线
的平分线 交
交 于F,点E是
于F,点E是 的中点,连接
的中点,连接 .
.
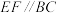 ;
;(2)若四边形
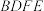 的面积为6,求
的面积为6,求 的面积.
的面积.
您最近一年使用:0次

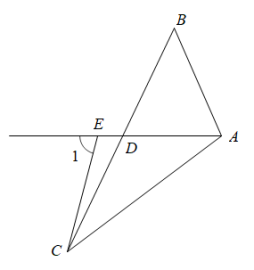
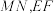 是两个互相平行的镜面,根据镜面反射规律:若一束光线
是两个互相平行的镜面,根据镜面反射规律:若一束光线 上,反射光线为
上,反射光线为 .光线
.光线
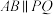 ,猜想
,猜想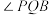 与
与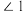 的数量关系,并说明理由.
的数量关系,并说明理由.
 .
.
 .
.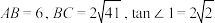 ,求
,求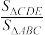 的值.
的值.


