综合与探究
如图,抛物线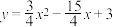 与x轴交于A,B两点,且点A在点B的左侧,与y轴交于点C.
与x轴交于A,B两点,且点A在点B的左侧,与y轴交于点C.
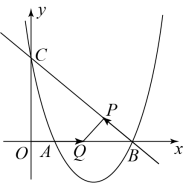
(1)求点A,B和C的坐标;
(2)点P从点B出发沿 以1个单位长度/秒的速度向终点C运动,同时,点Q从点O出发以相同的速度沿x轴的正半轴向终点B运动,一点到达,两点同时停止运动.连接
以1个单位长度/秒的速度向终点C运动,同时,点Q从点O出发以相同的速度沿x轴的正半轴向终点B运动,一点到达,两点同时停止运动.连接 ,当
,当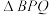 是等腰三角形时,请直接写出运动的时间.
是等腰三角形时,请直接写出运动的时间.
如图,抛物线
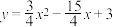 与x轴交于A,B两点,且点A在点B的左侧,与y轴交于点C.
与x轴交于A,B两点,且点A在点B的左侧,与y轴交于点C.
(1)求点A,B和C的坐标;
(2)点P从点B出发沿
 以1个单位长度/秒的速度向终点C运动,同时,点Q从点O出发以相同的速度沿x轴的正半轴向终点B运动,一点到达,两点同时停止运动.连接
以1个单位长度/秒的速度向终点C运动,同时,点Q从点O出发以相同的速度沿x轴的正半轴向终点B运动,一点到达,两点同时停止运动.连接 ,当
,当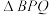 是等腰三角形时,请直接写出运动的时间.
是等腰三角形时,请直接写出运动的时间.
2022九年级上·全国·专题练习 查看更多[1]
(已下线)专题11 二次函数中的等腰三角形-【微专题】2022-2023学年九年级数学上册常考点微专题提分精练(人教版)
更新时间:2022/11/28 15:24:15
|
相似题推荐
解答题-问答题
|
适中
(0.65)
【推荐1】如图,抛物线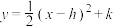 的顶点A是直线OD上一个动点,该抛物线与直线OD的另一个交点为C,与y轴的交点为B,点D的坐标是
的顶点A是直线OD上一个动点,该抛物线与直线OD的另一个交点为C,与y轴的交点为B,点D的坐标是 .
.
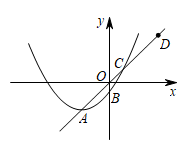
(1)求点B的纵坐标的最小值,并写出此时点A的坐标.
(2)在(1)的条件下,若该抛物线与x轴的两个交点分别为E和F,请直接写出线段EF的长度.
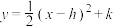 的顶点A是直线OD上一个动点,该抛物线与直线OD的另一个交点为C,与y轴的交点为B,点D的坐标是
的顶点A是直线OD上一个动点,该抛物线与直线OD的另一个交点为C,与y轴的交点为B,点D的坐标是 .
.
(1)求点B的纵坐标的最小值,并写出此时点A的坐标.
(2)在(1)的条件下,若该抛物线与x轴的两个交点分别为E和F,请直接写出线段EF的长度.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
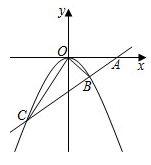
【推荐2】如图,已知直线 过
过 轴上一点
轴上一点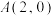 且与抛物线
且与抛物线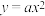 相交于
相交于 ,
, 两点.
两点.
(1)求抛物线对应的函数解析式;
(2)问抛物线上是否存在一点 ,使
,使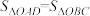 ?若存在,请求出
?若存在,请求出 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
 过
过 轴上一点
轴上一点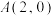 且与抛物线
且与抛物线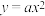 相交于
相交于 ,
, 两点.
两点.(1)求抛物线对应的函数解析式;
(2)问抛物线上是否存在一点
 ,使
,使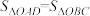 ?若存在,请求出
?若存在,请求出 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
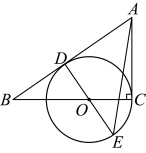
【推荐1】如图,在 中,
中, ,O为
,O为 边上一点,
边上一点, 过点C且经过
过点C且经过 边上的点D,
边上的点D, .
. 为
为 的切线;
的切线;
(2)延长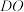 交
交 于点E,连接
于点E,连接 ,若
,若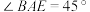 且
且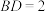 ,求
,求 的半径.
的半径.
 中,
中, ,O为
,O为 边上一点,
边上一点, 过点C且经过
过点C且经过 边上的点D,
边上的点D, .
.
 为
为 的切线;
的切线;(2)延长
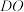 交
交 于点E,连接
于点E,连接 ,若
,若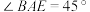 且
且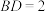 ,求
,求 的半径.
的半径.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
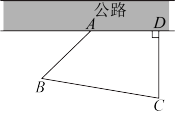
【推荐2】如图是某药厂的平面图,经测量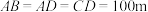 ,
,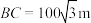 ,
,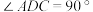 .
. 的度数;
的度数;
(2)已知 是药厂的进出口,为了能观察到进出口周围环境情况,工作人员计划在点B处安装一个摄像头,且摄像头能监控的最远距离为
是药厂的进出口,为了能观察到进出口周围环境情况,工作人员计划在点B处安装一个摄像头,且摄像头能监控的最远距离为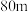 ,求直线
,求直线 上被摄像头监控的公路长度.
上被摄像头监控的公路长度.
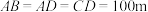 ,
,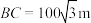 ,
,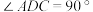 .
.
 的度数;
的度数;(2)已知
 是药厂的进出口,为了能观察到进出口周围环境情况,工作人员计划在点B处安装一个摄像头,且摄像头能监控的最远距离为
是药厂的进出口,为了能观察到进出口周围环境情况,工作人员计划在点B处安装一个摄像头,且摄像头能监控的最远距离为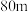 ,求直线
,求直线 上被摄像头监控的公路长度.
上被摄像头监控的公路长度.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
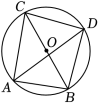
【推荐1】如图,已知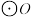 的直径为
的直径为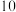 ,点
,点 ,点
,点 ,点
,点 在
在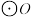 上,
上, 的平分线交
的平分线交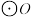 于点
于点 .若
.若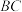 为
为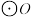 的直径,
的直径, ,求
,求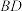 ,
,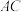 的长.
的长.
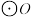 的直径为
的直径为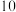 ,点
,点 ,点
,点 ,点
,点 在
在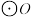 上,
上, 的平分线交
的平分线交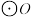 于点
于点 .若
.若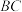 为
为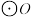 的直径,
的直径, ,求
,求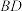 ,
,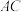 的长.
的长.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
名校
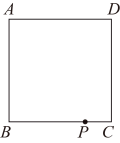
【推荐2】如图,正方形 是边长为4米的一块板材.
是边长为4米的一块板材.
操作一:现需从中裁出一个等腰直角 模具,点P在边
模具,点P在边 上,Q在正方形
上,Q在正方形 的内部或边上.
的内部或边上.
(1)如图,若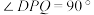 ,
,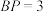 米,是否能裁出符合条件的
米,是否能裁出符合条件的 ?若能,确定Q的位置;若不能,请说明理由.
?若能,确定Q的位置;若不能,请说明理由.
(2)如图,连接 ,在对角线
,在对角线 上取点Q,连接
上取点Q,连接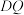 ,过点Q作
,过点Q作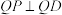 交边
交边 于P,连接
于P,连接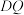 ,得到
,得到 .请证明
.请证明 符合裁剪要求.
符合裁剪要求.

操作二:经探究,操作一的模具大小至多为正方形面积的一半,现修改模具形状为四边形,并按面积要求进行裁剪.即在正方形 中重新裁出的一个四边形模具,点P、Q分别在边
中重新裁出的一个四边形模具,点P、Q分别在边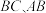 上.
上.
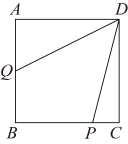
(3)如图,若需裁出的四边形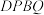 面积为10平方米,请探究模具四边形
面积为10平方米,请探究模具四边形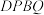 周长的最小值.
周长的最小值.
 是边长为4米的一块板材.
是边长为4米的一块板材.操作一:现需从中裁出一个等腰直角
 模具,点P在边
模具,点P在边 上,Q在正方形
上,Q在正方形 的内部或边上.
的内部或边上.(1)如图,若
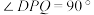 ,
,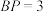 米,是否能裁出符合条件的
米,是否能裁出符合条件的 ?若能,确定Q的位置;若不能,请说明理由.
?若能,确定Q的位置;若不能,请说明理由.
(2)如图,连接
 ,在对角线
,在对角线 上取点Q,连接
上取点Q,连接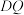 ,过点Q作
,过点Q作 交边
交边 于P,连接
于P,连接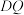 ,得到
,得到 .请证明
.请证明 符合裁剪要求.
符合裁剪要求.
操作二:经探究,操作一的模具大小至多为正方形面积的一半,现修改模具形状为四边形,并按面积要求进行裁剪.即在正方形
 中重新裁出的一个四边形模具,点P、Q分别在边
中重新裁出的一个四边形模具,点P、Q分别在边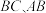 上.
上.(3)如图,若需裁出的四边形
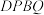 面积为10平方米,请探究模具四边形
面积为10平方米,请探究模具四边形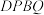 周长的最小值.
周长的最小值.
您最近一年使用:0次

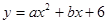 与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标分别为一元二次方程
与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标分别为一元二次方程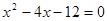 的两个根.
的两个根.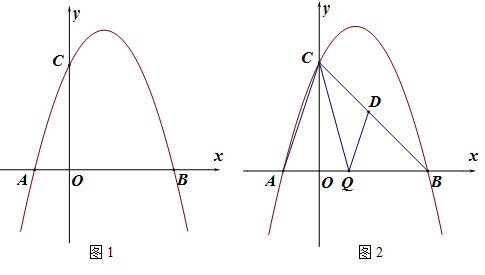
 ,点D为BC上一点,且
,点D为BC上一点,且 ,过A,B,D三点作⊙O,AE是⊙O的直径,连接DE.
,过A,B,D三点作⊙O,AE是⊙O的直径,连接DE.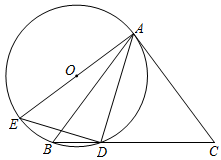
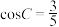 ,
,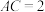 ,求直径AE的长.
,求直径AE的长.
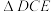 都是等腰直角三角形,
都是等腰直角三角形,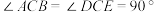 ,点
,点 三点在同一直线上,连结
三点在同一直线上,连结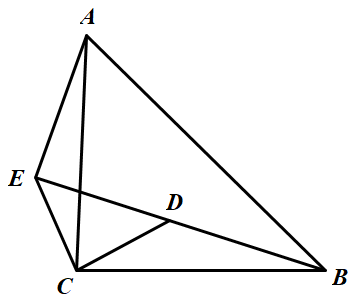
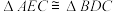 ;
; ,
,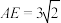 ,求
,求

