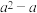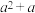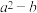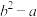在多项式 中,对相邻的两个字母间任意添加小括号,添加小括号后仍只有减法运算,然后将所得式子化简,称此为“有效操作”.例如:
中,对相邻的两个字母间任意添加小括号,添加小括号后仍只有减法运算,然后将所得式子化简,称此为“有效操作”.例如:
 ,
, ,…,给出下列说法:
,…,给出下列说法:
①存在“有效操作”,使其运算结果与原多项式相等;
②不存在“有效操作”,使其运算结果与原多项式之和为0;
③所有的“有效操作”共有8种不同运算结果.
其中正确的个数是( )
 中,对相邻的两个字母间任意添加小括号,添加小括号后仍只有减法运算,然后将所得式子化简,称此为“有效操作”.例如:
中,对相邻的两个字母间任意添加小括号,添加小括号后仍只有减法运算,然后将所得式子化简,称此为“有效操作”.例如:
 ,
, ,…,给出下列说法:
,…,给出下列说法:①存在“有效操作”,使其运算结果与原多项式相等;
②不存在“有效操作”,使其运算结果与原多项式之和为0;
③所有的“有效操作”共有8种不同运算结果.
其中正确的个数是( )
| A.0 | B.1 | C.2 | D.3 |
更新时间:2023/10/18 11:36:40
|
相似题推荐
单选题
|
较难
(0.4)
名校
解题方法
【推荐1】任何一个正整数n都可以进行这样的分解:n=p×q(p,q都是正整数,且p≤q),如果p×q在n的所有分解中两个因数之差的绝对值最小,我们就称p×q是n的黄金分解,并规定:F(n)=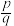 ,例如:18可以分解为1×18;2×9;3×6这三种,这时F(18)=
,例如:18可以分解为1×18;2×9;3×6这三种,这时F(18)=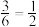 ,现给出下列关于F(n)的说法:①F(2) =
,现给出下列关于F(n)的说法:①F(2) = ;② F(24)=
;② F(24)=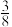 ;③F(27)=3;④若n是一个完全平方数,则F(n)=1,其中说法正确的个数有( )
;③F(27)=3;④若n是一个完全平方数,则F(n)=1,其中说法正确的个数有( )
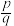 ,例如:18可以分解为1×18;2×9;3×6这三种,这时F(18)=
,例如:18可以分解为1×18;2×9;3×6这三种,这时F(18)=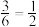 ,现给出下列关于F(n)的说法:①F(2) =
,现给出下列关于F(n)的说法:①F(2) = ;② F(24)=
;② F(24)=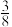 ;③F(27)=3;④若n是一个完全平方数,则F(n)=1,其中说法正确的个数有( )
;③F(27)=3;④若n是一个完全平方数,则F(n)=1,其中说法正确的个数有( )| A.1个 | B.2个 | C.3个 | D.4个 |
您最近一年使用:0次
单选题
|
较难
(0.4)
名校
【推荐2】现定义对于一个数a,我们把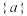 称为a的“邻一数”;若
称为a的“邻一数”;若 ,则
,则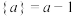 ;若
;若 ,则
,则 .例如:
.例如: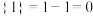 ,
, .下列说法,其中正确结论有( )个
.下列说法,其中正确结论有( )个
①若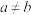 ,则
,则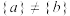 ;
;
②当 ,
,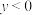 时,
时, ,那么代数式
,那么代数式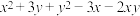 的值为4;
的值为4;
③方程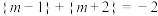 的解为
的解为 或
或 或
或 ;
;
④若函数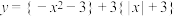 ,当
,当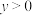 时,x的取值范围是
时,x的取值范围是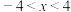 .
.
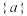 称为a的“邻一数”;若
称为a的“邻一数”;若 ,则
,则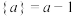 ;若
;若 ,则
,则 .例如:
.例如: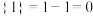 ,
, .下列说法,其中正确结论有( )个
.下列说法,其中正确结论有( )个①若
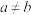 ,则
,则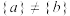 ;
;②当
 ,
,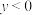 时,
时, ,那么代数式
,那么代数式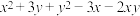 的值为4;
的值为4;③方程
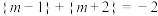 的解为
的解为 或
或 或
或 ;
;④若函数
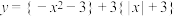 ,当
,当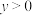 时,x的取值范围是
时,x的取值范围是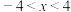 .
.| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
单选题
|
较难
(0.4)
名校
【推荐1】在多项式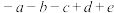 (其中
(其中 )中,对相邻的两个字母间添加绝对值符号,对相邻的两个或者三个字母间添加括号,每一次操作必须同时添加一个绝对值符号和一个括号,且添加绝对值符号和添加括号时不能有相同字母,然后进行去绝对值和去括号运算,称此为“双添操作”.例如:
)中,对相邻的两个字母间添加绝对值符号,对相邻的两个或者三个字母间添加括号,每一次操作必须同时添加一个绝对值符号和一个括号,且添加绝对值符号和添加括号时不能有相同字母,然后进行去绝对值和去括号运算,称此为“双添操作”.例如: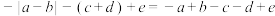 ,
,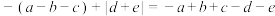 ,
, .
.
下列说法:①不存在“双添操作”,使其运算结果与原多项式相等;
②存在“双添操作”,使其运算结果与原多项式之和为0;
③所有的“双添操作”共有6种不同运算结果.
其中正确的个数是( )
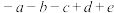 (其中
(其中 )中,对相邻的两个字母间添加绝对值符号,对相邻的两个或者三个字母间添加括号,每一次操作必须同时添加一个绝对值符号和一个括号,且添加绝对值符号和添加括号时不能有相同字母,然后进行去绝对值和去括号运算,称此为“双添操作”.例如:
)中,对相邻的两个字母间添加绝对值符号,对相邻的两个或者三个字母间添加括号,每一次操作必须同时添加一个绝对值符号和一个括号,且添加绝对值符号和添加括号时不能有相同字母,然后进行去绝对值和去括号运算,称此为“双添操作”.例如: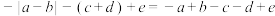 ,
,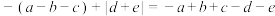 ,
, .
.下列说法:①不存在“双添操作”,使其运算结果与原多项式相等;
②存在“双添操作”,使其运算结果与原多项式之和为0;
③所有的“双添操作”共有6种不同运算结果.
其中正确的个数是( )
| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
单选题
|
较难
(0.4)
名校
【推荐2】对任意代数式,每个字母及其左边的符号(不包括括号外的符号)称为一个数,如: ,其中称
,其中称 为“数1”,
为“数1”, 为“数2”,
为“数2”,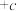 为“数3”,
为“数3”,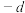 为“数4”,
为“数4”, 为“数5”,若将任意两个数交换位置,则称这个过程为“换位思考”,例如:对上述代数式的“数1”和“数5”进行“换位思考”,得到:
为“数5”,若将任意两个数交换位置,则称这个过程为“换位思考”,例如:对上述代数式的“数1”和“数5”进行“换位思考”,得到: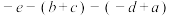 ,则下列说法中正确的个数是( )
,则下列说法中正确的个数是( )
①代数式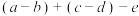 进行一次“换位思考”,化简后只能得到1种结果
进行一次“换位思考”,化简后只能得到1种结果
②代数式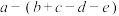 进行一次“换位思考”,化简后可能得到5种结果
进行一次“换位思考”,化简后可能得到5种结果
③代数式 进行一次“换位思考”,化简后可能得到7种结果
进行一次“换位思考”,化简后可能得到7种结果
④代数式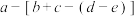 进行一次“换位思考”,化简后可能得到8种结果
进行一次“换位思考”,化简后可能得到8种结果
 ,其中称
,其中称 为“数1”,
为“数1”, 为“数2”,
为“数2”,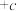 为“数3”,
为“数3”,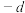 为“数4”,
为“数4”, 为“数5”,若将任意两个数交换位置,则称这个过程为“换位思考”,例如:对上述代数式的“数1”和“数5”进行“换位思考”,得到:
为“数5”,若将任意两个数交换位置,则称这个过程为“换位思考”,例如:对上述代数式的“数1”和“数5”进行“换位思考”,得到: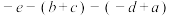 ,则下列说法中正确的个数是( )
,则下列说法中正确的个数是( )①代数式
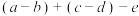 进行一次“换位思考”,化简后只能得到1种结果
进行一次“换位思考”,化简后只能得到1种结果②代数式
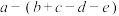 进行一次“换位思考”,化简后可能得到5种结果
进行一次“换位思考”,化简后可能得到5种结果③代数式
 进行一次“换位思考”,化简后可能得到7种结果
进行一次“换位思考”,化简后可能得到7种结果④代数式
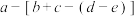 进行一次“换位思考”,化简后可能得到8种结果
进行一次“换位思考”,化简后可能得到8种结果| A.0 | B.2 | C.3 | D.4 |
您最近一年使用:0次

 ,满足
,满足 ,对这个多项式任意添加绝对值运算后仍然只含有减法运算,并将所得式子化简,称为“取正数运算”.例如:
,对这个多项式任意添加绝对值运算后仍然只含有减法运算,并将所得式子化简,称为“取正数运算”.例如: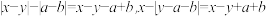 ,…,下列说法正确的个数为(
,…,下列说法正确的个数为( ,其中
,其中 都是有理数,则
都是有理数,则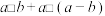 等于
等于