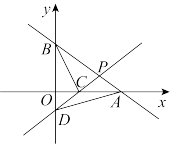
如图,点A,B的坐标分别为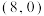 ,
, ,点P是线段
,点P是线段 上的一个动点,过点P的直线
上的一个动点,过点P的直线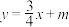 交x轴于点C,交y轴于点D,连接
交x轴于点C,交y轴于点D,连接 .
.
(1)求直线 的表达式;
的表达式;
(2)当 是直角三角形时,求m的值;
是直角三角形时,求m的值;
(3)在点P的运动过程中,探索并说明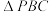 和
和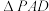 面积的数量关系.
面积的数量关系.
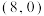 ,
, ,点P是线段
,点P是线段 上的一个动点,过点P的直线
上的一个动点,过点P的直线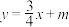 交x轴于点C,交y轴于点D,连接
交x轴于点C,交y轴于点D,连接 .
.
(1)求直线
 的表达式;
的表达式;(2)当
 是直角三角形时,求m的值;
是直角三角形时,求m的值;(3)在点P的运动过程中,探索并说明
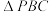 和
和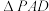 面积的数量关系.
面积的数量关系.
更新时间:2024/02/25 11:48:06
|
相似题推荐
解答题-问答题
|
较难
(0.4)
【推荐1】如图,直线y=-x+4与x轴、y轴分别交于A、B两点,直线BC与x轴、y轴分别交于C、B两点,连接BC,且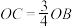 .
.
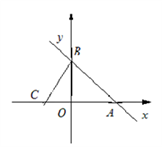
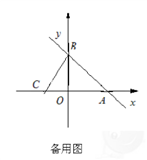

(1)求点A的坐标及直线BC的函数关系式;
(2)点M在x轴上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;
(3)若点P在x轴上,平面内是否存在点Q,使点B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
 .
.


(1)求点A的坐标及直线BC的函数关系式;
(2)点M在x轴上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;
(3)若点P在x轴上,平面内是否存在点Q,使点B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
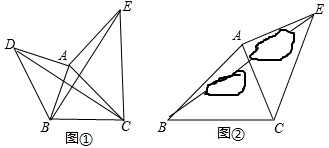
【推荐2】如图①所示,直线L:yax10a与x轴负半轴、y轴正半轴分别交于A、B两点.

(1)当OAOB时,试确定直线L的解析式;
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AMOQ于M,BNOQ于N,若AM8,BN6,求MN的长.
(3)当a取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角OBF和等腰直角ABE,连接EF交y轴于P点,如图③,问:当点B在y轴正半轴上运动时,试猜想PB的长是否为定值,若是,请求出其值,若不是,说明理由.

(1)当OAOB时,试确定直线L的解析式;
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AMOQ于M,BNOQ于N,若AM8,BN6,求MN的长.
(3)当a取不同的值时,点B在y轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角OBF和等腰直角ABE,连接EF交y轴于P点,如图③,问:当点B在y轴正半轴上运动时,试猜想PB的长是否为定值,若是,请求出其值,若不是,说明理由.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
【推荐3】在平面直角坐标系 中,点M的坐标为
中,点M的坐标为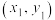 ,点N的坐标为
,点N的坐标为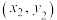 ,且
,且 ,
,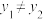 ,若
,若 ,
, 为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点
为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点 ,
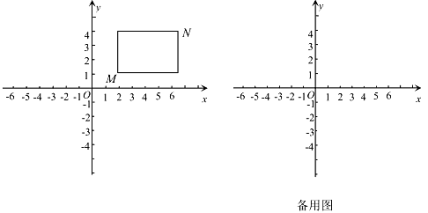
, 的“标准矩形”,如图为点
的“标准矩形”,如图为点 ,
, 的“标准矩形”示意图.
的“标准矩形”示意图.
(1)已知点 的坐标为
的坐标为 ,
,
①点 为直线
为直线 图象上第一象限内的一点,且点
图象上第一象限内的一点,且点 ,
, 的“标准矩形”的两邻边长的比为1∶2,求点
的“标准矩形”的两邻边长的比为1∶2,求点 的坐标;
的坐标;
②点 在直线
在直线 上,若点
上,若点 ,
, 的“标准矩形”为正方形,求直线
的“标准矩形”为正方形,求直线 的表达式;
的表达式;
(2) 的半径为2,点
的半径为2,点 的坐标为
的坐标为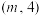 ,若在
,若在 上存在一点
上存在一点 ,使得点
,使得点 ,
, 的“标准矩形”为正方形,直接写出
的“标准矩形”为正方形,直接写出 的取值范围.
的取值范围.
 中,点M的坐标为
中,点M的坐标为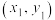 ,点N的坐标为
,点N的坐标为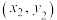 ,且
,且 ,
,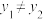 ,若
,若 ,
, 为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点
为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点 ,
, 的“标准矩形”,如图为点
的“标准矩形”,如图为点 ,
, 的“标准矩形”示意图.
的“标准矩形”示意图.
(1)已知点
 的坐标为
的坐标为 ,
,①点
 为直线
为直线 图象上第一象限内的一点,且点
图象上第一象限内的一点,且点 ,
, 的“标准矩形”的两邻边长的比为1∶2,求点
的“标准矩形”的两邻边长的比为1∶2,求点 的坐标;
的坐标;②点
 在直线
在直线 上,若点
上,若点 ,
, 的“标准矩形”为正方形,求直线
的“标准矩形”为正方形,求直线 的表达式;
的表达式;(2)
 的半径为2,点
的半径为2,点 的坐标为
的坐标为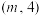 ,若在
,若在 上存在一点
上存在一点 ,使得点
,使得点 ,
, 的“标准矩形”为正方形,直接写出
的“标准矩形”为正方形,直接写出 的取值范围.
的取值范围.
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
【推荐1】在正方形 中,点E为边
中,点E为边 上一点(不与点C、D重合),
上一点(不与点C、D重合), 于点F,
于点F, 于点G.
于点G. ;
;
(2)如图2,若F为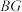 中点,连接
中点,连接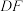 ,用等式表示线段
,用等式表示线段 ,
,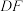 之间的数量关系,并证明;
之间的数量关系,并证明;
(3)若 ,
,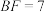 ,求线段
,求线段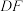 的长;
的长;
(4)若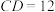 ,点M为
,点M为 的中点,点N在
的中点,点N在 边上,
边上,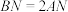 ,在图3 中画出
,在图3 中画出 , 并求
, 并求 的度数.
的度数.
 中,点E为边
中,点E为边 上一点(不与点C、D重合),
上一点(不与点C、D重合), 于点F,
于点F, 于点G.
于点G.
 ;
;(2)如图2,若F为
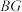 中点,连接
中点,连接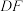 ,用等式表示线段
,用等式表示线段 ,
,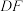 之间的数量关系,并证明;
之间的数量关系,并证明;(3)若
 ,
,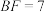 ,求线段
,求线段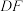 的长;
的长;(4)若
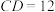 ,点M为
,点M为 的中点,点N在
的中点,点N在 边上,
边上,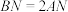 ,在图3 中画出
,在图3 中画出 , 并求
, 并求 的度数.
的度数.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
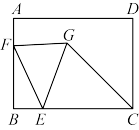
【推荐2】如图,长方形 中,
中,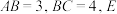 为
为 上一点,且
上一点,且 为
为 边上的一个动点,连接
边上的一个动点,连接 ,将
,将 绕着点
绕着点 顺时针旋转
顺时针旋转 到
到 的位置,连接
的位置,连接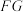 和
和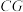 ,问
,问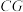 是否有最小值?如果有,求出
是否有最小值?如果有,求出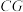 的最小值.
的最小值.
 中,
中,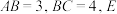 为
为 上一点,且
上一点,且 为
为 边上的一个动点,连接
边上的一个动点,连接 ,将
,将 绕着点
绕着点 顺时针旋转
顺时针旋转 到
到 的位置,连接
的位置,连接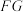 和
和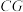 ,问
,问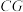 是否有最小值?如果有,求出
是否有最小值?如果有,求出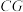 的最小值.
的最小值. 
您最近一年使用:0次