如图,在平面直角坐标系 中,点
中,点 ,
, ,其中
,其中 ,点
,点 在第四象限内,
在第四象限内, 交
交 轴于点
轴于点 .且
.且 ,
, ,连接
,连接 ,并作
,并作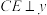 轴于点
轴于点 .
.

(1)求证: ;
;
(2)求点 的坐标;(用含
的坐标;(用含 的式子表示)
的式子表示)
(3)如图1,过点 作直线
作直线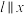 轴,过点
轴,过点 作
作 于点
于点 ,求证:直线
,求证:直线 ,直线
,直线 ,直线
,直线 相交于一点.
相交于一点.
 中,点
中,点 ,
, ,其中
,其中 ,点
,点 在第四象限内,
在第四象限内, 交
交 轴于点
轴于点 .且
.且 ,
, ,连接
,连接 ,并作
,并作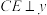 轴于点
轴于点 .
.
(1)求证:
 ;
;(2)求点
 的坐标;(用含
的坐标;(用含 的式子表示)
的式子表示)(3)如图1,过点
 作直线
作直线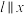 轴,过点
轴,过点 作
作 于点
于点 ,求证:直线
,求证:直线 ,直线
,直线 ,直线
,直线 相交于一点.
相交于一点.
更新时间:2024/03/03 15:18:55
|
相似题推荐
解答题-问答题
|
适中
(0.65)
【推荐1】如图,一次函数.  与反比例函数
与反比例函数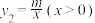 的图象交于
的图象交于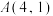 ,
, 两点.
两点.
(2)点P在线段 上,过点P作x轴的垂线,垂足为M,交函数
上,过点P作x轴的垂线,垂足为M,交函数 的图象于点 Q,若
的图象于点 Q,若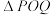 面积为3,求点P的坐标.
面积为3,求点P的坐标.
 与反比例函数
与反比例函数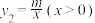 的图象交于
的图象交于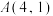 ,
, 两点.
两点.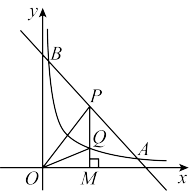
(2)点P在线段
 上,过点P作x轴的垂线,垂足为M,交函数
上,过点P作x轴的垂线,垂足为M,交函数 的图象于点 Q,若
的图象于点 Q,若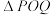 面积为3,求点P的坐标.
面积为3,求点P的坐标.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
名校
【推荐2】如图,一次函数y=kx+1的图象与反比例函数y=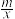 的图象交于点A、B,点A在第一象限,过点A作AC⊥x轴于点C,AD⊥y轴于点D,点B的纵坐标为-2,一次函数的图象分别交x轴、y轴于点E、F,连接DB、DE,已知S△ADF=4,AC=3OF.
的图象交于点A、B,点A在第一象限,过点A作AC⊥x轴于点C,AD⊥y轴于点D,点B的纵坐标为-2,一次函数的图象分别交x轴、y轴于点E、F,连接DB、DE,已知S△ADF=4,AC=3OF.
(2)直接写出反比例函数的值大于一次函数的值的x的取值范围.
(3)在x轴上是否存在点P,使 .若存在,求出Р点坐标;若不存在,请说明理由.
.若存在,求出Р点坐标;若不存在,请说明理由.
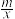 的图象交于点A、B,点A在第一象限,过点A作AC⊥x轴于点C,AD⊥y轴于点D,点B的纵坐标为-2,一次函数的图象分别交x轴、y轴于点E、F,连接DB、DE,已知S△ADF=4,AC=3OF.
的图象交于点A、B,点A在第一象限,过点A作AC⊥x轴于点C,AD⊥y轴于点D,点B的纵坐标为-2,一次函数的图象分别交x轴、y轴于点E、F,连接DB、DE,已知S△ADF=4,AC=3OF.
(2)直接写出反比例函数的值大于一次函数的值的x的取值范围.
(3)在x轴上是否存在点P,使
 .若存在,求出Р点坐标;若不存在,请说明理由.
.若存在,求出Р点坐标;若不存在,请说明理由.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
【推荐3】某数学学习网站,正在讲解如下问题:

【背景呈现】在平面直角坐标系中,直线 经过
经过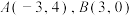 ,直线
,直线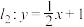 与
与 轴交于点
轴交于点 ,与直线
,与直线 交于点
交于点
【解决问题】
(1)求直线 的函数解析式;
的函数解析式;
(2)求 的面积;
的面积;
【拓展探究】嘉淇为了更好观看图像,用手机截屏该问题的图像,如图所示,嘉淇发现屏幕上有一位置固定的黑点 ,刚好落在直角坐标系中坐标为
,刚好落在直角坐标系中坐标为 的位置上,嘉淇通过手机的触屏功能,在坐标原点的位置与可视范围不改变的情况下,把截屏横向、纵向放大相同的倍数,当直线
的位置上,嘉淇通过手机的触屏功能,在坐标原点的位置与可视范围不改变的情况下,把截屏横向、纵向放大相同的倍数,当直线 恰好经过点
恰好经过点 时,图中坐标系的单位长度变为原来的
时,图中坐标系的单位长度变为原来的 倍,直接写出
倍,直接写出 的值;
的值;

【背景呈现】在平面直角坐标系中,直线
 经过
经过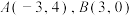 ,直线
,直线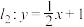 与
与 轴交于点
轴交于点 ,与直线
,与直线 交于点
交于点
【解决问题】
(1)求直线
 的函数解析式;
的函数解析式;(2)求
 的面积;
的面积;【拓展探究】嘉淇为了更好观看图像,用手机截屏该问题的图像,如图所示,嘉淇发现屏幕上有一位置固定的黑点
 ,刚好落在直角坐标系中坐标为
,刚好落在直角坐标系中坐标为 的位置上,嘉淇通过手机的触屏功能,在坐标原点的位置与可视范围不改变的情况下,把截屏横向、纵向放大相同的倍数,当直线
的位置上,嘉淇通过手机的触屏功能,在坐标原点的位置与可视范围不改变的情况下,把截屏横向、纵向放大相同的倍数,当直线 恰好经过点
恰好经过点 时,图中坐标系的单位长度变为原来的
时,图中坐标系的单位长度变为原来的 倍,直接写出
倍,直接写出 的值;
的值;
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
【推荐1】如图所示,直线AB、CD、EF相交于点O,且AB⊥CD,OG平分∠AOE,若∠DOF=50°,求∠AOG的度数.


您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
名校
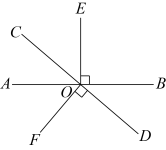
【推荐2】如图,直线 与
与 相交于点
相交于点 ,
,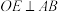 ,
, .
. 互余的角是___________;(把符合条件的角都写出来)
互余的角是___________;(把符合条件的角都写出来)
(2)如果 ,求
,求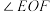 的度数.
的度数.
 与
与 相交于点
相交于点 ,
,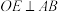 ,
, .
.
 互余的角是___________;(把符合条件的角都写出来)
互余的角是___________;(把符合条件的角都写出来)(2)如果
 ,求
,求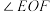 的度数.
的度数.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
【推荐1】如图,在 中,
中, 于点D.
于点D.
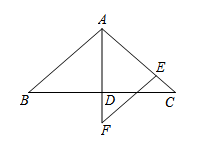
(1)若 ,求
,求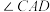 的度数;
的度数;
(2)若点E在边 上,
上, 交
交 的延长线于点F.求证:
的延长线于点F.求证: .
.
 中,
中, 于点D.
于点D.
(1)若
 ,求
,求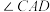 的度数;
的度数;(2)若点E在边
 上,
上, 交
交 的延长线于点F.求证:
的延长线于点F.求证: .
.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
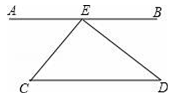
【推荐2】如图,AB∥CD,∠CED=90°,∠BED=40°,求∠C的度数.

您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
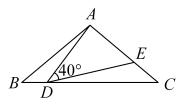
【推荐1】如图,在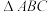 中,
中, ,
, ,点D在线段
,点D在线段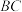 上运动(D不与B、C重合),连接
上运动(D不与B、C重合),连接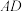 ,作
,作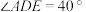 ,
, 交线段
交线段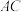 于E.
于E.
(1)当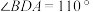 时,
时,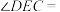 °;点D从B向C运动时,
°;点D从B向C运动时,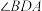 逐渐变 (填“大”或“小”);
逐渐变 (填“大”或“小”);
(2)当 为何值时,
为何值时, ,并说明理由;
,并说明理由;
(3)在点D的运动过程中,若 是等腰三角形,求
是等腰三角形,求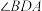 的度数.
的度数.
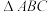 中,
中, ,
, ,点D在线段
,点D在线段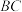 上运动(D不与B、C重合),连接
上运动(D不与B、C重合),连接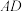 ,作
,作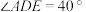 ,
, 交线段
交线段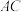 于E.
于E.
(1)当
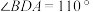 时,
时,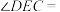 °;点D从B向C运动时,
°;点D从B向C运动时,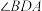 逐渐变 (填“大”或“小”);
逐渐变 (填“大”或“小”);(2)当
 为何值时,
为何值时, ,并说明理由;
,并说明理由;(3)在点D的运动过程中,若
 是等腰三角形,求
是等腰三角形,求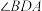 的度数.
的度数.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
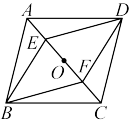
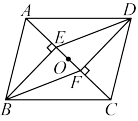
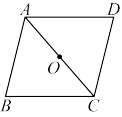
【推荐2】如图,在平行四边形 中,点O是对角线AC的中点.某数学学习小组要在
中,点O是对角线AC的中点.某数学学习小组要在 上找两点E,F,使四边形
上找两点E,F,使四边形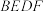 为平行四边形,现在,甲、乙两个同学给出了两种不同的方案如下:
为平行四边形,现在,甲、乙两个同学给出了两种不同的方案如下:
请回答下列问题:
(1)你认为按照他们两人的方案得到的四边形是平行四边形吗?如果这两种方案得到的四边形都是平行四边形,请选择一种给出证明.如果哪种方案不可行,请说明理由.
(2)请你给出一种和他们不同的方案.并说明这三种方案有什么共同的特征.
 中,点O是对角线AC的中点.某数学学习小组要在
中,点O是对角线AC的中点.某数学学习小组要在 上找两点E,F,使四边形
上找两点E,F,使四边形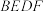 为平行四边形,现在,甲、乙两个同学给出了两种不同的方案如下:
为平行四边形,现在,甲、乙两个同学给出了两种不同的方案如下:| 甲方案 | 乙方案 | 我的方案 |
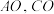 的中点E,F 的中点E,F |
 于点E, 于点E,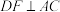 于点F 于点F |
|
(1)你认为按照他们两人的方案得到的四边形是平行四边形吗?如果这两种方案得到的四边形都是平行四边形,请选择一种给出证明.如果哪种方案不可行,请说明理由.
(2)请你给出一种和他们不同的方案.并说明这三种方案有什么共同的特征.
您最近一年使用:0次

 平分
平分 ,
,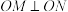 .
.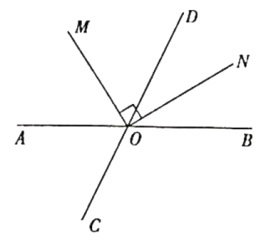
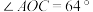 ,求
,求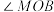 的度数;
的度数; 平分
平分 .
.
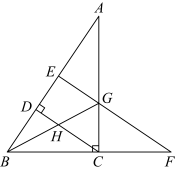
 中,
中,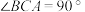 ,
,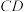 是斜边上的高,点G是
是斜边上的高,点G是 和
和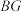 ,交
,交 .
.
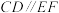 ;
; ,试说明
,试说明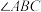 .
.