1 . 已知①设函数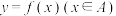 的值域是
的值域是 ,对于
,对于 中的每个
中的每个 ,若函数
,若函数 在每一处
在每一处 都等于它对应的
都等于它对应的 ,这样的函数
,这样的函数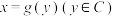 叫做函数
叫做函数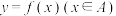 的反函数,记作
的反函数,记作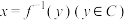 ,我们习惯记自变量为
,我们习惯记自变量为 ,因此
,因此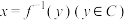 可改成
可改成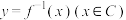 即为原函数的反函数.易知
即为原函数的反函数.易知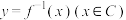 与
与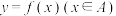 互为反函数,且
互为反函数,且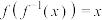 .如
.如 的反函数是
的反函数是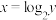 可改写成
可改写成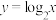 即为
即为 的反函数,
的反函数,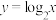 与
与 互为反函数.②
互为反函数.② 是定义在
是定义在 且取值于
且取值于 的一个函数,定义
的一个函数,定义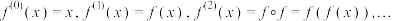
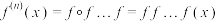 ,则称
,则称 是函数
是函数 在
在 上的
上的 次迭代.例如
次迭代.例如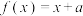 ,则
,则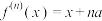 .对于一些相对复杂的函数,为求出其
.对于一些相对复杂的函数,为求出其 次迭代函数,我们引入如下一种关系:对于给定的函数
次迭代函数,我们引入如下一种关系:对于给定的函数 和
和 ,若函数
,若函数 的反函数
的反函数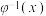 存在,且有
存在,且有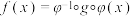 ,称
,称 与
与 关于
关于 相似,记作
相似,记作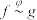 ,其中
,其中 称为桥函数,桥函数满足以下性质:
称为桥函数,桥函数满足以下性质:
(i)若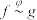 ,则
,则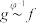
(ii)若 为
为 的一个不动点,即
的一个不动点,即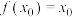 ,则
,则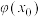 为
为 的一个不动点.
的一个不动点.
(1)若函数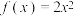 ,求
,求 (写出结果即可)
(写出结果即可)
(2)证明:若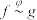 ,则
,则 .
.
(3)若函数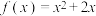 ,求
,求 (桥函数可选取
(桥函数可选取 ),若
),若 ,试选取恰当桥函数,计算
,试选取恰当桥函数,计算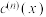 .
.
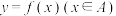 的值域是
的值域是 ,对于
,对于 中的每个
中的每个 ,若函数
,若函数 在每一处
在每一处 都等于它对应的
都等于它对应的 ,这样的函数
,这样的函数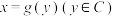 叫做函数
叫做函数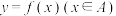 的反函数,记作
的反函数,记作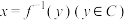 ,我们习惯记自变量为
,我们习惯记自变量为 ,因此
,因此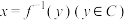 可改成
可改成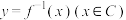 即为原函数的反函数.易知
即为原函数的反函数.易知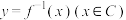 与
与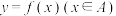 互为反函数,且
互为反函数,且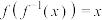 .如
.如 的反函数是
的反函数是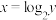 可改写成
可改写成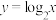 即为
即为 的反函数,
的反函数,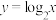 与
与 互为反函数.②
互为反函数.② 是定义在
是定义在 且取值于
且取值于 的一个函数,定义
的一个函数,定义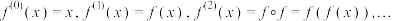
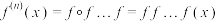 ,则称
,则称 是函数
是函数 在
在 上的
上的 次迭代.例如
次迭代.例如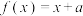 ,则
,则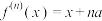 .对于一些相对复杂的函数,为求出其
.对于一些相对复杂的函数,为求出其 次迭代函数,我们引入如下一种关系:对于给定的函数
次迭代函数,我们引入如下一种关系:对于给定的函数 和
和 ,若函数
,若函数 的反函数
的反函数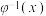 存在,且有
存在,且有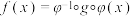 ,称
,称 与
与 关于
关于 相似,记作
相似,记作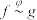 ,其中
,其中 称为桥函数,桥函数满足以下性质:
称为桥函数,桥函数满足以下性质:(i)若
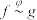 ,则
,则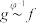
(ii)若
 为
为 的一个不动点,即
的一个不动点,即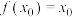 ,则
,则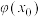 为
为 的一个不动点.
的一个不动点.(1)若函数
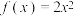 ,求
,求 (写出结果即可)
(写出结果即可)(2)证明:若
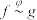 ,则
,则 .
.(3)若函数
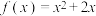 ,求
,求 (桥函数可选取
(桥函数可选取 ),若
),若 ,试选取恰当桥函数,计算
,试选取恰当桥函数,计算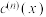 .
.
您最近一年使用:0次
2 . 一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
(1)(归纳奠基)证明当 时命题成立;
时命题成立;
(2)(归纳递推)以“当 时命题成立”为条件,推出“当
时命题成立”为条件,推出“当 时命题也成立”.
时命题也成立”.
只要完成这两个步骤,就可以断定命题对从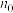 开始的所有正整数n都成立,这种证明方法称为数学归纳法.
开始的所有正整数n都成立,这种证明方法称为数学归纳法.
已知集合A为有理数集Q的一个子集,且满足以下条件:
①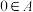 且
且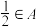 ;
;
②对任意的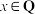 ,存在唯一的
,存在唯一的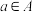 ,满足
,满足 ,其中
,其中 ,
,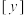 表示不超过y的最大整数;
表示不超过y的最大整数;
③若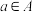 ,
, ,则
,则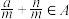 .
.
证明:
(1) ;
;
(2)对任意的 ,对每一个整数
,对每一个整数 ,都有
,都有 ;
;
(3) .
.
(1)(归纳奠基)证明当
 时命题成立;
时命题成立;(2)(归纳递推)以“当
 时命题成立”为条件,推出“当
时命题成立”为条件,推出“当 时命题也成立”.
时命题也成立”.只要完成这两个步骤,就可以断定命题对从
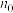 开始的所有正整数n都成立,这种证明方法称为数学归纳法.
开始的所有正整数n都成立,这种证明方法称为数学归纳法.已知集合A为有理数集Q的一个子集,且满足以下条件:
①
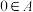 且
且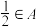 ;
;②对任意的
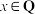 ,存在唯一的
,存在唯一的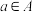 ,满足
,满足 ,其中
,其中 ,
,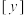 表示不超过y的最大整数;
表示不超过y的最大整数;③若
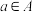 ,
, ,则
,则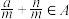 .
.证明:
(1)
 ;
;(2)对任意的
 ,对每一个整数
,对每一个整数 ,都有
,都有 ;
;(3)
 .
.
您最近一年使用:0次



