已知抛物线 的焦点为F,准线为l;
的焦点为F,准线为l;
(1)若F为双曲线 的一个焦点,求双曲线C的离心率e;
的一个焦点,求双曲线C的离心率e;
(2)设l与x轴的交点为E,点P在第一象限,且在 上,若
上,若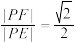 ,求直线EP的方程;
,求直线EP的方程;
(3)经过点F且斜率为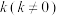 的直线l'与
的直线l'与 相交于A,B两点,O为坐标原点,直线
相交于A,B两点,O为坐标原点,直线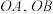 分别与l相交于点M,N;试探究:以线段MN为直径的圆C是否过定点;若是,求出定点的坐标;若不是,说明理由;
分别与l相交于点M,N;试探究:以线段MN为直径的圆C是否过定点;若是,求出定点的坐标;若不是,说明理由;
 的焦点为F,准线为l;
的焦点为F,准线为l;(1)若F为双曲线
 的一个焦点,求双曲线C的离心率e;
的一个焦点,求双曲线C的离心率e;(2)设l与x轴的交点为E,点P在第一象限,且在
 上,若
上,若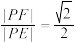 ,求直线EP的方程;
,求直线EP的方程;(3)经过点F且斜率为
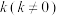 的直线l'与
的直线l'与 相交于A,B两点,O为坐标原点,直线
相交于A,B两点,O为坐标原点,直线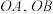 分别与l相交于点M,N;试探究:以线段MN为直径的圆C是否过定点;若是,求出定点的坐标;若不是,说明理由;
分别与l相交于点M,N;试探究:以线段MN为直径的圆C是否过定点;若是,求出定点的坐标;若不是,说明理由;
2023·上海长宁·一模 查看更多[4]
上海市长宁区2023届高三上学期一模数学试题上海市奉贤区致远高级中学2022-2023学年高二下学期3月教学评估数学试题上海市复兴高级中学2024届高三上学期开学考试数学试题(已下线)上海市高二下学期期末真题必刷04(压轴题)--高二期末考点大串讲(沪教版2020选修)
更新时间:2022/12/15 23:34:08
|
相似题推荐
解答题-问答题
|
适中
(0.65)
名校
【推荐1】已知双曲线 :
: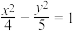 .
.
(1)求双曲线的离心率 与渐近线方程;
与渐近线方程;
(2)若椭圆 与双曲线有相同的焦点且经过点
与双曲线有相同的焦点且经过点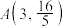 ,求椭圆
,求椭圆 的标准方程.
的标准方程.
 :
: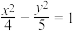 .
.(1)求双曲线的离心率
 与渐近线方程;
与渐近线方程;(2)若椭圆
 与双曲线有相同的焦点且经过点
与双曲线有相同的焦点且经过点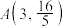 ,求椭圆
,求椭圆 的标准方程.
的标准方程.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
解题方法
【推荐2】已知椭圆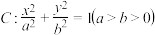 经过点
经过点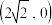 ,且
,且 的离心率与双曲线
的离心率与双曲线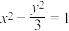 的离心率互为倒数.
的离心率互为倒数.
(1)求 的方程;
的方程;
(2)若直线 与
与 交于
交于 ,
, 两点,点
两点,点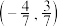 是弦
是弦 的中点,求直线
的中点,求直线 的方程.
的方程.
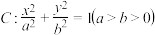 经过点
经过点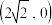 ,且
,且 的离心率与双曲线
的离心率与双曲线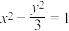 的离心率互为倒数.
的离心率互为倒数.(1)求
 的方程;
的方程;(2)若直线
 与
与 交于
交于 ,
, 两点,点
两点,点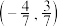 是弦
是弦 的中点,求直线
的中点,求直线 的方程.
的方程.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
名校
解题方法
【推荐1】已知抛物线 的焦点为
的焦点为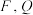 为
为 上一点且纵坐标为4,
上一点且纵坐标为4,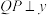 轴于点
轴于点 ,且
,且 .
.
(1)求 的值;
的值;
(2)已知点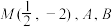 是抛物线
是抛物线 上不同的两点,且满足
上不同的两点,且满足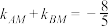 .证明:直线
.证明:直线 恒过定点.
恒过定点.
 的焦点为
的焦点为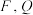 为
为 上一点且纵坐标为4,
上一点且纵坐标为4,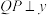 轴于点
轴于点 ,且
,且 .
.(1)求
 的值;
的值;(2)已知点
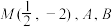 是抛物线
是抛物线 上不同的两点,且满足
上不同的两点,且满足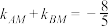 .证明:直线
.证明:直线 恒过定点.
恒过定点.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
名校
解题方法
【推荐2】设抛物线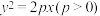 的焦点为
的焦点为 ,点
,点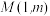 在抛物线上,且
在抛物线上,且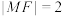 ,椭圆
,椭圆 右焦点也为
右焦点也为 ,离心率为
,离心率为 .
.
(1)求抛物线方程和椭圆方程;
(2)若不经过 的直线与抛物线交于
的直线与抛物线交于 、
、 两点,且
两点,且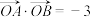 (
( 为坐标原点),直线与椭圆交于
为坐标原点),直线与椭圆交于 、
、 两点,求
两点,求 面积的最大值.
面积的最大值.
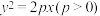 的焦点为
的焦点为 ,点
,点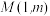 在抛物线上,且
在抛物线上,且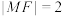 ,椭圆
,椭圆 右焦点也为
右焦点也为 ,离心率为
,离心率为 .
.(1)求抛物线方程和椭圆方程;
(2)若不经过
 的直线与抛物线交于
的直线与抛物线交于 、
、 两点,且
两点,且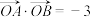 (
( 为坐标原点),直线与椭圆交于
为坐标原点),直线与椭圆交于 、
、 两点,求
两点,求 面积的最大值.
面积的最大值.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
名校
解题方法
【推荐1】已知抛物线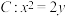 ,直线
,直线 与抛物线
与抛物线 交于
交于 ,
, 两点,分别过
两点,分别过 ,
, 作抛物线
作抛物线 的切线,两切线交于点
的切线,两切线交于点 .
.
(1)若直线 变动时,点
变动时,点 始终在以
始终在以 为直径的圆上,求动点
为直径的圆上,求动点 的轨迹方程;
的轨迹方程;
(2)设圆 ,若直线
,若直线 与圆
与圆 相切于点
相切于点 (点
(点 在线段
在线段 上).是否存在点
上).是否存在点 使得
使得 ?若存在,求出点
?若存在,求出点 坐标,若不存在,说明理由.
坐标,若不存在,说明理由.
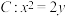 ,直线
,直线 与抛物线
与抛物线 交于
交于 ,
, 两点,分别过
两点,分别过 ,
, 作抛物线
作抛物线 的切线,两切线交于点
的切线,两切线交于点 .
.(1)若直线
 变动时,点
变动时,点 始终在以
始终在以 为直径的圆上,求动点
为直径的圆上,求动点 的轨迹方程;
的轨迹方程;(2)设圆
 ,若直线
,若直线 与圆
与圆 相切于点
相切于点 (点
(点 在线段
在线段 上).是否存在点
上).是否存在点 使得
使得 ?若存在,求出点
?若存在,求出点 坐标,若不存在,说明理由.
坐标,若不存在,说明理由.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
名校
解题方法
【推荐2】已知动圆 过定点
过定点 ,且与直线
,且与直线 相切.
相切.
(1)求动圆圆心 的轨迹
的轨迹 的方程;
的方程;
(2)直线 过点
过点 与曲线
与曲线 相交于
相交于 两点,问:在
两点,问:在 轴上是否存在定点
轴上是否存在定点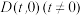 ,使
,使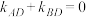 ?若存在,求点
?若存在,求点 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由.
 过定点
过定点 ,且与直线
,且与直线 相切.
相切.(1)求动圆圆心
 的轨迹
的轨迹 的方程;
的方程;(2)直线
 过点
过点 与曲线
与曲线 相交于
相交于 两点,问:在
两点,问:在 轴上是否存在定点
轴上是否存在定点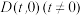 ,使
,使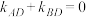 ?若存在,求点
?若存在,求点 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由.
您最近一年使用:0次

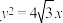 的焦点也是椭圆
的焦点也是椭圆 的右焦点,而
的右焦点,而 的离心率的倒数
的离心率的倒数 中,
中,
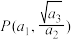 在椭圆
在椭圆
 的前
的前 项和
项和
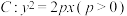 上一点
上一点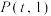 到其焦点
到其焦点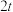 .
.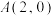 ,动直线
,动直线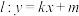 与抛物线
与抛物线 两点,若直线
两点,若直线 与直线
与直线 的倾斜角互补,求证:直线
的倾斜角互补,求证:直线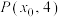 在抛物线C上,且
在抛物线C上,且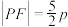
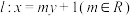 与抛物线C相交于
与抛物线C相交于 两点,问:在x轴上是否存在定点
两点,问:在x轴上是否存在定点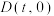 (其中
(其中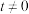 ),使得x轴平分
),使得x轴平分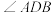 ?若存在,求出点D的坐标;若不存在,请说明理由.
?若存在,求出点D的坐标;若不存在,请说明理由.


