已知 为坐标原点,动点
为坐标原点,动点 在椭圆
在椭圆 上,动点
上,动点 满足
满足 ,记点
,记点 的轨迹为
的轨迹为
(1)求轨迹 的方程;
的方程;
(2)在轨迹 上是否存在点
上是否存在点 ,使得过点
,使得过点 作椭圆
作椭圆 的两条切线互相垂直?若存在,求点
的两条切线互相垂直?若存在,求点 的坐标:若不存在,请说明理由:
的坐标:若不存在,请说明理由:
(3)过点 的直线
的直线 交轨迹
交轨迹 于
于 ,
, 两点,射线
两点,射线 交轨迹
交轨迹 于点
于点 ,射线
,射线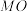 交椭圆
交椭圆 于点
于点 ,求四边形
,求四边形 面积的最大值.
面积的最大值.
 为坐标原点,动点
为坐标原点,动点 在椭圆
在椭圆 上,动点
上,动点 满足
满足 ,记点
,记点 的轨迹为
的轨迹为
(1)求轨迹
 的方程;
的方程;(2)在轨迹
 上是否存在点
上是否存在点 ,使得过点
,使得过点 作椭圆
作椭圆 的两条切线互相垂直?若存在,求点
的两条切线互相垂直?若存在,求点 的坐标:若不存在,请说明理由:
的坐标:若不存在,请说明理由:(3)过点
 的直线
的直线 交轨迹
交轨迹 于
于 ,
, 两点,射线
两点,射线 交轨迹
交轨迹 于点
于点 ,射线
,射线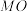 交椭圆
交椭圆 于点
于点 ,求四边形
,求四边形 面积的最大值.
面积的最大值.
更新时间:2024/05/14 18:07:29
|
相似题推荐
解答题-问答题
|
较难
(0.4)
名校
解题方法
【推荐1】已知点 是圆
是圆 上的动点,过点
上的动点,过点 作
作 轴的垂线段PD,D为垂足,点
轴的垂线段PD,D为垂足,点 满足
满足 ,当点
,当点 运动时,设点
运动时,设点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)若过点 且斜率为
且斜率为 的直线
的直线 与曲线
与曲线 交于A,B两点.
交于A,B两点.
(i)求 的取值范围;
的取值范围;
(ii)求 面积的最大值.
面积的最大值.
 是圆
是圆 上的动点,过点
上的动点,过点 作
作 轴的垂线段PD,D为垂足,点
轴的垂线段PD,D为垂足,点 满足
满足 ,当点
,当点 运动时,设点
运动时,设点 的轨迹为曲线
的轨迹为曲线 .
.(1)求曲线
 的方程;
的方程;(2)若过点
 且斜率为
且斜率为 的直线
的直线 与曲线
与曲线 交于A,B两点.
交于A,B两点.(i)求
 的取值范围;
的取值范围;(ii)求
 面积的最大值.
面积的最大值.
您最近一年使用:0次
【推荐2】如图所示,圆O: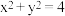 ,
,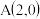 ,
,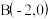 ,D为圆O上任意一点,过D作圆O的切线分别交直线
,D为圆O上任意一点,过D作圆O的切线分别交直线 和
和 于E,F两点,连AF,BE交于点G,若点G形成的轨迹为曲线C.
于E,F两点,连AF,BE交于点G,若点G形成的轨迹为曲线C.

 记AF,BE斜率分别为
记AF,BE斜率分别为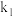 ,
,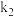 ,求
,求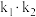 的值并求曲线C的方程;
的值并求曲线C的方程;
 设直线l:
设直线l: 与曲线C有两个不同的交点P,Q,与直线
与曲线C有两个不同的交点P,Q,与直线 交于点S,与直线
交于点S,与直线 交于点T,求
交于点T,求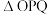 的面积与
的面积与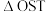 面积的比值
面积的比值 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
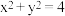 ,
,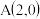 ,
,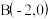 ,D为圆O上任意一点,过D作圆O的切线分别交直线
,D为圆O上任意一点,过D作圆O的切线分别交直线 和
和 于E,F两点,连AF,BE交于点G,若点G形成的轨迹为曲线C.
于E,F两点,连AF,BE交于点G,若点G形成的轨迹为曲线C.
 记AF,BE斜率分别为
记AF,BE斜率分别为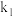 ,
,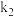 ,求
,求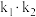 的值并求曲线C的方程;
的值并求曲线C的方程; 设直线l:
设直线l: 与曲线C有两个不同的交点P,Q,与直线
与曲线C有两个不同的交点P,Q,与直线 交于点S,与直线
交于点S,与直线 交于点T,求
交于点T,求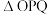 的面积与
的面积与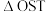 面积的比值
面积的比值 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
您最近一年使用:0次
【推荐1】(1)试证在中心为O点的椭圆上任取两点P、Q,使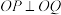 ,则
,则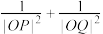 与P、Q点的选取无关.
与P、Q点的选取无关.
(2)在(1)的条件下求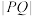 的最小值;并求
的最小值;并求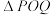 面积的最小值.
面积的最小值.
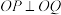 ,则
,则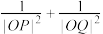 与P、Q点的选取无关.
与P、Q点的选取无关.(2)在(1)的条件下求
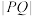 的最小值;并求
的最小值;并求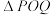 面积的最小值.
面积的最小值.
您最近一年使用:0次
【推荐2】已知椭圆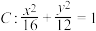 ,右焦点
,右焦点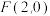 ,直线
,直线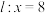 ,过右焦点
,过右焦点 的直线(不与
的直线(不与 轴重合)与椭圆
轴重合)与椭圆 交于
交于 两点,过点
两点,过点 作
作 ,垂足为
,垂足为 .
.
(1)求证:直线 过定点
过定点 ,并求出定点
,并求出定点 的坐标;
的坐标;
(2)点 为坐标原点,求
为坐标原点,求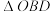 面积的最大值.
面积的最大值.
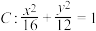 ,右焦点
,右焦点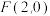 ,直线
,直线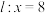 ,过右焦点
,过右焦点 的直线(不与
的直线(不与 轴重合)与椭圆
轴重合)与椭圆 交于
交于 两点,过点
两点,过点 作
作 ,垂足为
,垂足为 .
.(1)求证:直线
 过定点
过定点 ,并求出定点
,并求出定点 的坐标;
的坐标;(2)点
 为坐标原点,求
为坐标原点,求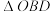 面积的最大值.
面积的最大值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
解题方法
【推荐1】如图,已知椭圆 的左、右两个焦点分别为
的左、右两个焦点分别为 、
、 ,左、右顶点分别为
,左、右顶点分别为 、
、 ,离心率为
,离心率为 ,过
,过 的动直线
的动直线 与椭圆
与椭圆 交于
交于 、
、 两点,且
两点,且 的周长为
的周长为 .
.
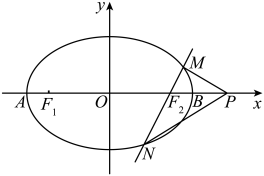
(1)求椭圆 的标准方程;
的标准方程;
(2)在 轴上是否存在点
轴上是否存在点 ,使得
,使得 (
( 为坐标原点),若存在,求出点
为坐标原点),若存在,求出点 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由.
 的左、右两个焦点分别为
的左、右两个焦点分别为 、
、 ,左、右顶点分别为
,左、右顶点分别为 、
、 ,离心率为
,离心率为 ,过
,过 的动直线
的动直线 与椭圆
与椭圆 交于
交于 、
、 两点,且
两点,且 的周长为
的周长为 .
.
(1)求椭圆
 的标准方程;
的标准方程;(2)在
 轴上是否存在点
轴上是否存在点 ,使得
,使得 (
( 为坐标原点),若存在,求出点
为坐标原点),若存在,求出点 坐标,若不存在,请说明理由.
坐标,若不存在,请说明理由.
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
名校
解题方法
【推荐2】已知椭圆 的离心率为
的离心率为 ,左、右顶点分别为
,左、右顶点分别为 ,点P是椭圆上的动点,且点P与点
,点P是椭圆上的动点,且点P与点 不重合,过其右焦点F与长轴垂直的直线与椭圆在第一象限交于点M,且
不重合,过其右焦点F与长轴垂直的直线与椭圆在第一象限交于点M,且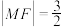 .
.
(1)求椭圆C的方程;
(2)设直线 的斜率分别为
的斜率分别为 ,且与直线
,且与直线 分别交于点
分别交于点 ,
,
①求: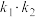 的值;
的值;
②求证:以线段 为直径的圆过左焦点
为直径的圆过左焦点 ,并求当圆的面积最小时
,并求当圆的面积最小时 的值.
的值.
 的离心率为
的离心率为 ,左、右顶点分别为
,左、右顶点分别为 ,点P是椭圆上的动点,且点P与点
,点P是椭圆上的动点,且点P与点 不重合,过其右焦点F与长轴垂直的直线与椭圆在第一象限交于点M,且
不重合,过其右焦点F与长轴垂直的直线与椭圆在第一象限交于点M,且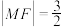 .
.(1)求椭圆C的方程;
(2)设直线
 的斜率分别为
的斜率分别为 ,且与直线
,且与直线 分别交于点
分别交于点 ,
,①求:
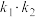 的值;
的值;②求证:以线段
 为直径的圆过左焦点
为直径的圆过左焦点 ,并求当圆的面积最小时
,并求当圆的面积最小时 的值.
的值.
您最近一年使用:0次

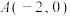 、
、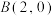 ,直线
,直线 、
、 相交于点
相交于点 .
. ,直线
,直线 、
、 与圆
与圆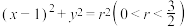 相切于点
相切于点 ,求
,求 的面积的最大值(其中点
的面积的最大值(其中点 ,抛物线
,抛物线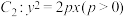 ,点A是椭圆
,点A是椭圆 与抛物线
与抛物线 的一个交点,过点A的直线l交椭圆
的一个交点,过点A的直线l交椭圆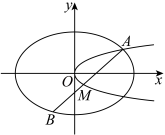
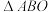 面积的最大值及此时直线l的方程;
面积的最大值及此时直线l的方程; 是椭圆
是椭圆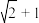 .
.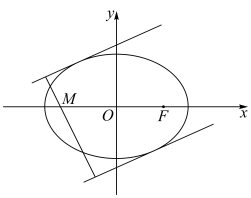
 ,
,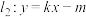 ,若
,若 均与椭圆
均与椭圆

