名校
1 . 设集合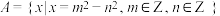 .
.
(1)求证:所有奇数均属于集合A
(2)用反证法证明:10不是集合 的元素.
的元素.
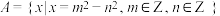 .
.(1)求证:所有奇数均属于集合A
(2)用反证法证明:10不是集合
 的元素.
的元素.
您最近一年使用:0次
2 . 如图,在 中,
中, ,
, 为
为 边上的一点,以
边上的一点,以 为直径的
为直径的 交
交 于点
于点 ,过点
,过点 作
作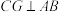 交
交 于点
于点 ,交
,交 于点
于点 ,过点
,过点 作
作 交
交 于点
于点 ,
, .
. 是
是 的切线;
的切线;
(2)连接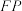 ,试猜想四边形
,试猜想四边形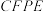 的形状,并加以证明;
的形状,并加以证明;
(3)若 ,求四边形
,求四边形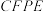 的面积.
的面积.
 中,
中, ,
, 为
为 边上的一点,以
边上的一点,以 为直径的
为直径的 交
交 于点
于点 ,过点
,过点 作
作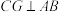 交
交 于点
于点 ,交
,交 于点
于点 ,过点
,过点 作
作 交
交 于点
于点 ,
, .
.
 是
是 的切线;
的切线;(2)连接
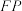 ,试猜想四边形
,试猜想四边形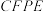 的形状,并加以证明;
的形状,并加以证明;(3)若
 ,求四边形
,求四边形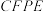 的面积.
的面积.
您最近一年使用:0次
3 . 下面图片是八年级教科书中的一道题:如图,四边形 是正方形,点
是正方形,点 是边
是边 的中点,
的中点,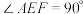 ,且
,且 交正方形外角的平分线
交正方形外角的平分线 于点
于点 .求证
.求证 .(提示:取
.(提示:取 的中点
的中点 ,连接)
,连接) .
.
(2)如图1,若点 是
是 边上任意一点(不与
边上任意一点(不与 重合),其他条件不变.求证:
重合),其他条件不变.求证: ;
;
(3)在(2)的条件下,连接 ,过点
,过点 作
作 ,垂足为
,垂足为 .设
.设 ,当
,当 为何值时,四边形
为何值时,四边形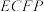 是平行四边形,并给予证明,
是平行四边形,并给予证明,
 是正方形,点
是正方形,点 是边
是边 的中点,
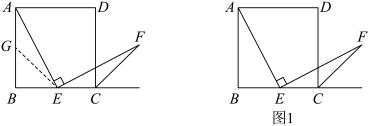
的中点,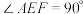 ,且
,且 交正方形外角的平分线
交正方形外角的平分线 于点
于点 .求证
.求证 .(提示:取
.(提示:取 的中点
的中点 ,连接)
,连接) .
.
(2)如图1,若点
 是
是 边上任意一点(不与
边上任意一点(不与 重合),其他条件不变.求证:
重合),其他条件不变.求证: ;
;(3)在(2)的条件下,连接
 ,过点
,过点 作
作 ,垂足为
,垂足为 .设
.设 ,当
,当 为何值时,四边形
为何值时,四边形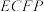 是平行四边形,并给予证明,
是平行四边形,并给予证明,
您最近一年使用:0次
名校
4 . 如图, 是矩形
是矩形 的对角线,
的对角线, 的平分线
的平分线 交
交 于点
于点 .
.
(1)用尺规完成以下基本作图:作 的平分线交
的平分线交 于点
于点 ;连接
;连接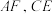 ;(不写作法和证明,保留作图痕迹)
;(不写作法和证明,保留作图痕迹)
(2)在(1)所作的图形中,求证:四边形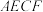 是平行四边形.(请补全下面的证明过程,除题目给的字母外,不添加其它字母或者符号)
是平行四边形.(请补全下面的证明过程,除题目给的字母外,不添加其它字母或者符号)
证明: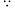 四边形
四边形 是矩形,
是矩形,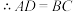 ,①_____.
,①_____.
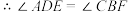 ,
,
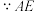 平分
平分 平分
平分 ,
,
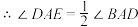 ,
,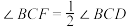 ,
,
 四边形
四边形 是矩形,
是矩形,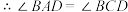 .
.
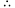 ②_____.
②_____.
 .
.
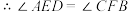 ,③_____.
,③_____.
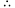 ④_____.
④_____.
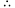 四边形
四边形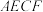 是平行四边形,
是平行四边形,
 是矩形
是矩形 的对角线,
的对角线, 的平分线
的平分线 交
交 于点
于点 .
.(1)用尺规完成以下基本作图:作
 的平分线交
的平分线交 于点
于点 ;连接
;连接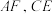 ;(不写作法和证明,保留作图痕迹)
;(不写作法和证明,保留作图痕迹)(2)在(1)所作的图形中,求证:四边形
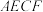 是平行四边形.(请补全下面的证明过程,除题目给的字母外,不添加其它字母或者符号)
是平行四边形.(请补全下面的证明过程,除题目给的字母外,不添加其它字母或者符号)证明:
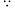 四边形
四边形 是矩形,
是矩形,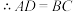 ,①_____.
,①_____.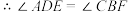 ,
,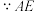 平分
平分 平分
平分 ,
,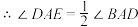 ,
,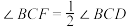 ,
, 四边形
四边形 是矩形,
是矩形,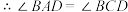 .
.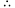 ②_____.
②_____. .
.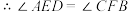 ,③_____.
,③_____.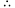 ④_____.
④_____.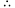 四边形
四边形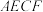 是平行四边形,
是平行四边形,
您最近一年使用:0次
名校
5 . 小南在学习矩形的判定之后,想继续研究判定一个平行四边形是矩形的方法,他的想法是作平行四边形两相邻内角的角平分线,与两内角公共边的对边相交,如果这相邻内角的顶点到对应交点的距离相等,则可论证该平行四边形是矩形.
(1)用直尺和圆规,作射线 平分
平分 交
交 于点
于点 ;
;
(2)已知:如图,在平行四边形 中,
中, 平分
平分 交
交 于点
于点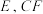 平分
平分 交
交 于点
于点 ,且
,且 .求证:平行四边形
.求证:平行四边形 是矩形.
是矩形.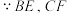 分别平分
分别平分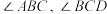 ,
,
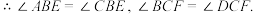
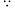 四边形
四边形 为平行四边形,
为平行四边形,


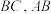

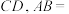 __________①,
__________①,
 ,
,
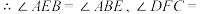 __________②,
__________②,
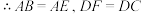 ,
,
 ,
,
在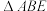 和
和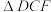 中
中
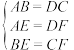


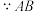


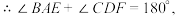
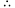 __________③.
__________③.
 平行四边形
平行四边形 是矩形.
是矩形.
小南再进一步研究发现,若这组邻角的角平分线与公共边的对边延长线相交,结论仍然成立.因此,小南得出结论:作平行四边形两相邻内角的角平分线,与两内角公共边的对边(或对边延长线)相交,若这相邻内角的顶点到对应交点的距离相等,则_ _________④.
(1)用直尺和圆规,作射线
 平分
平分 交
交 于点
于点 ;
;(2)已知:如图,在平行四边形
 中,
中, 平分
平分 交
交 于点
于点 平分
平分 交
交 于点
于点 ,且
,且 .求证:平行四边形
.求证:平行四边形 是矩形.
是矩形.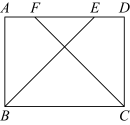
 分别平分
分别平分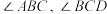 ,
,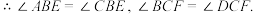
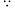 四边形
四边形 为平行四边形,
为平行四边形,

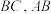

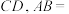 __________①,
__________①, ,
,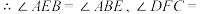 __________②,
__________②,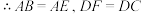 ,
, ,
,在
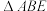 和
和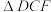 中
中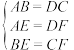


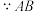


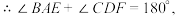
 __________③.
__________③. 平行四边形
平行四边形 是矩形.
是矩形.小南再进一步研究发现,若这组邻角的角平分线与公共边的对边延长线相交,结论仍然成立.因此,小南得出结论:作平行四边形两相邻内角的角平分线,与两内角公共边的对边(或对边延长线)相交,若这相邻内角的顶点到对应交点的距离相等,则_ _________④.
您最近一年使用:0次
6 . 已知:关于x的方程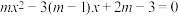 .
.
(1)求证:m取任何实数量,方程总有实数根;
(2)若二次函数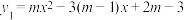 的图象关于y轴对称;
的图象关于y轴对称;
①求二次函数 的解析式;
的解析式;
②已知一次函数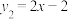 ,证明:在实数范围内,对于x的同一个值,这两个函数所对应的函数值
,证明:在实数范围内,对于x的同一个值,这两个函数所对应的函数值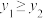 均成立.
均成立.
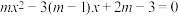 .
.(1)求证:m取任何实数量,方程总有实数根;
(2)若二次函数
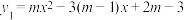 的图象关于y轴对称;
的图象关于y轴对称;①求二次函数
 的解析式;
的解析式;②已知一次函数
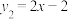 ,证明:在实数范围内,对于x的同一个值,这两个函数所对应的函数值
,证明:在实数范围内,对于x的同一个值,这两个函数所对应的函数值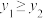 均成立.
均成立.
您最近一年使用:0次
7 . 已知:如图,等腰三角形 中,
中, ,
, ,直线
,直线 经过点
经过点 (点
(点 、
、 都在直线
都在直线 的同侧),
的同侧), ,
,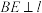 ,垂足分别为
,垂足分别为 、
、 .
.

(1)求证: ;
;
(2)请判断 、
、 、
、 三条线段之间有怎样的数量关系,并证明.
三条线段之间有怎样的数量关系,并证明.
 中,
中, ,
, ,直线
,直线 经过点
经过点 (点
(点 、
、 都在直线
都在直线 的同侧),
的同侧), ,
,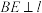 ,垂足分别为
,垂足分别为 、
、 .
.
(1)求证:
 ;
;(2)请判断
 、
、 、
、 三条线段之间有怎样的数量关系,并证明.
三条线段之间有怎样的数量关系,并证明.
您最近一年使用:0次
名校
解题方法
8 . 如图,在三棱柱 中,若G,H分别是线段AC,DF的中点.
中,若G,H分别是线段AC,DF的中点.

 ;
;
(2)在线段CD上是否存在一点 ,使得平面
,使得平面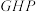
 平面BCF,若存在,指出
平面BCF,若存在,指出 的具体位置并证明;若不存在,说明理由.
的具体位置并证明;若不存在,说明理由.
 中,若G,H分别是线段AC,DF的中点.
中,若G,H分别是线段AC,DF的中点.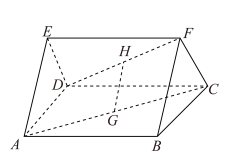


 ;
;(2)在线段CD上是否存在一点
 ,使得平面
,使得平面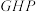
 平面BCF,若存在,指出
平面BCF,若存在,指出 的具体位置并证明;若不存在,说明理由.
的具体位置并证明;若不存在,说明理由.
您最近一年使用:0次
2023-04-13更新
|
3311次组卷
|
11卷引用:浙江省宁波市三锋教研联盟2022-2023学年高一下学期期中联考数学试题
浙江省宁波市三锋教研联盟2022-2023学年高一下学期期中联考数学试题(已下线)立体几何专题:立体几何探索性问题的8种考法(已下线)13.2.4 平面与平面的位置关系 (1)河北定州中学2022-2023学年高一下学期5月月考数学试题江西省宜春市第十中学2024届高二上学期开学检测数学试题新疆阿克苏市实验中学2022-2023学年高一下学期第三次月考数学试题(已下线)8.5.3 平面与平面平行【第三练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)11.3.3平面与平面平行-同步精品课堂(人教B版2019必修第四册)(已下线)专题突破:空间几何体的动点探究问题-同步题型分类归纳讲与练(人教A版2019必修第二册)【课后练】第4.4节综合训练 课后作业-湘教版(2019)必修(第二册) 第4章 立体几何初步(已下线)第四节直线、平面平行的判定与性质【同步课时】基础卷
9 . 下图是小明复习全等三角形时遇到的一个问题并引发的思考,请帮助小明完成以下学习任务.
如图,OC平分 ,点P在OC上,M、N分别是
,点P在OC上,M、N分别是 、OB上的点,
、OB上的点, ,求证:
,求证: .
.
小明的思考:要证明 ,只需证明
,只需证明 即可.
即可.
证法:如图①:∵OC平分 ,∴
,∴ ,
,
又∵ ,
, ,∴
,∴ ,
,
∴ ;
;
请仔细阅读并完成以下任务: 的依据是______(填序号).
的依据是______(填序号).
①SSS ②SAS ③AAS ④ASA ⑤HL
(2)如图②,在四边形ABCD中, ,
,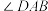 的平分线和
的平分线和 的平分线交于CD边上点P,求证:
的平分线交于CD边上点P,求证: .
.
(3)在(2)的条件下,如图③,若 ,
,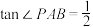 ,当△PBC有一个内角是45°时,
,当△PBC有一个内角是45°时,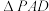 的面积是______.
的面积是______.
如图,OC平分
 ,点P在OC上,M、N分别是
,点P在OC上,M、N分别是 、OB上的点,
、OB上的点, ,求证:
,求证: .
.小明的思考:要证明
 ,只需证明
,只需证明 即可.
即可.证法:如图①:∵OC平分
 ,∴
,∴ ,
,又∵
 ,
, ,∴
,∴ ,
,∴
 ;
;请仔细阅读并完成以下任务:
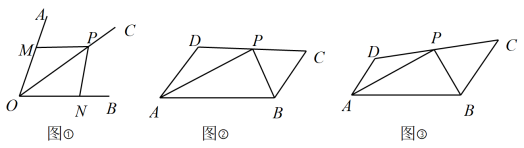
 的依据是______(填序号).
的依据是______(填序号).①SSS ②SAS ③AAS ④ASA ⑤HL
(2)如图②,在四边形ABCD中,
 ,
,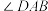 的平分线和
的平分线和 的平分线交于CD边上点P,求证:
的平分线交于CD边上点P,求证: .
.(3)在(2)的条件下,如图③,若
 ,
,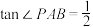 ,当△PBC有一个内角是45°时,
,当△PBC有一个内角是45°时,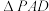 的面积是______.
的面积是______.
您最近一年使用:0次
10 . 请阅读下列材料,并完成相应的任务.
战国时的《墨经》就有“圆,一中同长也”的记载.与圆有关的定理有很多,弦切角定理就是其中之一.我们把顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.弦切角定理:弦切角的度数等于它所夹的弧所对的圆周角度数.
下面是弦切角定理的部分证明过程:
证明:①如图1,AB与 相切于点A.当圆心O在弦AC上时,容易得到
相切于点A.当圆心O在弦AC上时,容易得到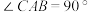 ,所以弦切角
,所以弦切角 .
.
②如图2,AB与 相切于点A.当圆心O在
相切于点A.当圆心O在 的外部时,过点A作直径AF交
的外部时,过点A作直径AF交 于点F,连接FC.
于点F,连接FC.
∵AF是直径,∴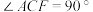 ,∴
,∴ .
.
∵AB与 相切于点A,∴
相切于点A,∴ ,∴
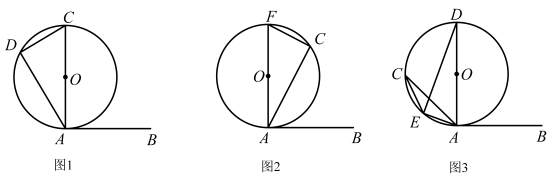
,∴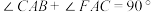 ,∴
,∴ .
.
(1)如图3,AB与 相切于点A,当圆心O在
相切于点A,当圆心O在 的内部时,过点A作直径AD交
的内部时,过点A作直径AD交 于点D,在
于点D,在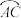 上任取一点E,连接EC,ED,EA,求证:
上任取一点E,连接EC,ED,EA,求证: ;
;
(2)如图3,已知 的半径为1,弦切角
的半径为1,弦切角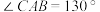 ,求
,求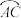 的长.
的长.
战国时的《墨经》就有“圆,一中同长也”的记载.与圆有关的定理有很多,弦切角定理就是其中之一.我们把顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.弦切角定理:弦切角的度数等于它所夹的弧所对的圆周角度数.
下面是弦切角定理的部分证明过程:
证明:①如图1,AB与
 相切于点A.当圆心O在弦AC上时,容易得到
相切于点A.当圆心O在弦AC上时,容易得到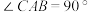 ,所以弦切角
,所以弦切角 .
.②如图2,AB与
 相切于点A.当圆心O在
相切于点A.当圆心O在 的外部时,过点A作直径AF交
的外部时,过点A作直径AF交 于点F,连接FC.
于点F,连接FC.∵AF是直径,∴
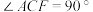 ,∴
,∴ .
.∵AB与
 相切于点A,∴
相切于点A,∴ ,∴
,∴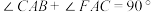 ,∴
,∴ .
.
(1)如图3,AB与
 相切于点A,当圆心O在
相切于点A,当圆心O在 的内部时,过点A作直径AD交
的内部时,过点A作直径AD交 于点D,在
于点D,在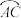 上任取一点E,连接EC,ED,EA,求证:
上任取一点E,连接EC,ED,EA,求证: ;
;(2)如图3,已知
 的半径为1,弦切角
的半径为1,弦切角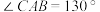 ,求
,求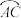 的长.
的长.
您最近一年使用:0次



