2019高三上·全国·专题练习
名校
解题方法
1 . 画糖是一种以糖为材料在石板上进行造型的民间艺术,常见于公园与旅游景点.某师傅制作了一种新造型糖画,为了进行合理定价先进行试销售,其单价 (元)与销量
(元)与销量 (个)的相关数据如下表:
(个)的相关数据如下表:
(1)已知销量 与单价
与单价 具有线性相关关系,求
具有线性相关关系,求 关于
关于 的线性相关方程;
的线性相关方程;
(2)若该新造型糖画每个的成本为 元,要使得进入售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
元,要使得进入售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
参考公式:线性回归方程 中斜率和截距的最小二乘法估计计算公式为
中斜率和截距的最小二乘法估计计算公式为 ,
, .
.
参考数据: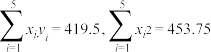 .
.
 (元)与销量
(元)与销量 (个)的相关数据如下表:
(个)的相关数据如下表:单价x(元) | 8.5 | 9 | 9.5 | 10 | 10.5 |
销量y(个) | 12 | 11 | 9 | 7 | 6 |
(1)已知销量
 与单价
与单价 具有线性相关关系,求
具有线性相关关系,求 关于
关于 的线性相关方程;
的线性相关方程;(2)若该新造型糖画每个的成本为
 元,要使得进入售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
元,要使得进入售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)参考公式:线性回归方程
 中斜率和截距的最小二乘法估计计算公式为
中斜率和截距的最小二乘法估计计算公式为 ,
, .
.参考数据:
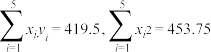 .
.
您最近一年使用:0次
2019-11-13更新
|
355次组卷
|
4卷引用:黑龙江省佳木斯市富锦市第一中学2022-2023学年高二下学期期末数学试题
黑龙江省佳木斯市富锦市第一中学2022-2023学年高二下学期期末数学试题(已下线)2019年11月15日 《每日一题》一轮复习理数-变量间的相关关系(已下线)2019年11月27日《每日一题》一轮复习文数-变量间的相关关系陕西省延安市第一中学2021-2022学年高一下学期期末数学试题
名校
解题方法
2 . 某莲藕种植塘每年的固定成本是2万元,每年最大规模的种植量是10万斤,每种植1斤藕,成本增加1元.销售额 (单位:万元)与莲藕种植量
(单位:万元)与莲藕种植量 (单位:万斤)满足
(单位:万斤)满足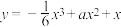 (
( 为常数),若种植3万斤,利润是
为常数),若种植3万斤,利润是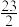 万元,则要使销售利润最大,每年需种植莲藕( )
万元,则要使销售利润最大,每年需种植莲藕( )
 (单位:万元)与莲藕种植量
(单位:万元)与莲藕种植量 (单位:万斤)满足
(单位:万斤)满足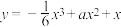 (
( 为常数),若种植3万斤,利润是
为常数),若种植3万斤,利润是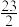 万元,则要使销售利润最大,每年需种植莲藕( )
万元,则要使销售利润最大,每年需种植莲藕( )| A.7万斤 | B.8万斤 | C.9万斤 | D.10万斤 |
您最近一年使用:0次
2024-04-10更新
|
350次组卷
|
8卷引用:黑龙江省牡丹江市第二高级中学2023-2024学年高二下学期第二次月考数学试卷
名校
3 . 近年来,网上购物已经成为人们消费的一种习惯.假设某淘宝店的一种装饰品每月的销售量 (单位:千件)与销售价格
(单位:千件)与销售价格 (单位:元/件)之间满足如下的关系式:
(单位:元/件)之间满足如下的关系式: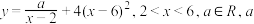 为常数.已知销售价格为
为常数.已知销售价格为 元/件时,每月可售出
元/件时,每月可售出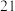 千件.
千件.
(1)求实数 的值;
的值;
(2)假设该淘宝店员工工资、办公等所有的成本折合为每件2元(只考虑销售出的装饰品件数),试确定销售价格 的值,使该店每月销售装饰品所获得的利润最大.(结果保留一位小数)
的值,使该店每月销售装饰品所获得的利润最大.(结果保留一位小数)
 (单位:千件)与销售价格
(单位:千件)与销售价格 (单位:元/件)之间满足如下的关系式:
(单位:元/件)之间满足如下的关系式: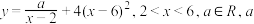 为常数.已知销售价格为
为常数.已知销售价格为 元/件时,每月可售出
元/件时,每月可售出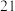 千件.
千件.(1)求实数
 的值;
的值; (2)假设该淘宝店员工工资、办公等所有的成本折合为每件2元(只考虑销售出的装饰品件数),试确定销售价格
 的值,使该店每月销售装饰品所获得的利润最大.(结果保留一位小数)
的值,使该店每月销售装饰品所获得的利润最大.(结果保留一位小数)
您最近一年使用:0次
2019-06-12更新
|
1450次组卷
|
5卷引用:【全国百强校】黑龙江省哈尔滨市第三中学校2018-2019学年高二下学期期中考试数学(理)试题
4 . 为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=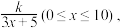 若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(Ⅰ)求k的值及f(x)的表达式.
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
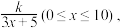 若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.(Ⅰ)求k的值及f(x)的表达式.
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
您最近一年使用:0次
2019-01-30更新
|
4443次组卷
|
130卷引用:2012-2013学年黑龙江省大庆铁人中学高二下学期期末考试文科数学卷
(已下线)2012-2013学年黑龙江省大庆铁人中学高二下学期期末考试文科数学卷【校级联考】黑龙江省哈尔滨市呼兰一中、阿城二中、宾县三中、尚志五中四校2018-2019学年高二下学期期中考试数学(理)试题(已下线)2012届黑龙江省大庆铁人中高三第一学期期末考试理科数学(已下线)2011—2012学年江苏省赣榆县厉庄高级中学度高二下期中文科数学试卷(已下线)2013-2014学年甘肃省兰州一中高二下学期期中考试理科数学试卷(已下线)2013-2014学年甘肃省兰州一中高二下学期期中考试文科数学试卷(已下线)2013-2014学年甘肃兰州一中高二下学期期中理科数学试卷(已下线)2013-2014学年甘肃兰州一中高二下学期期中文科数学试卷2015-2016学年内蒙古准格尔旗世纪中学高二下第一次月考理科数学卷2015-2016学年甘肃省武威民勤一中高二下期中理科数学试卷2015-2016年江西省上饶市铅山一中高二下期中理科数学试卷(已下线)同步君人教A版必修5第三章3.4 基本不等式2016-2017学年安徽六安一中高二理上学期周检八数学试卷2016-2017学年安徽省六安市第一中学高二下学期第一次阶段检测数学(理)试卷福建省泉州市南安第一中学2016-2017学年高二下学期期末考试数学(理)试题(已下线)2018年10月13日 《每日一题》人教必修5-周末培优人教版 全能练习 选修1-1【提分攻略】第四章 导数应用【校级联考】福建省厦门六中2018-2019学年高二(上)期中理科数学试题(已下线)2019年10月13日 每周一测-学易试题君之每日一题君2019-2020学年上学期高二数学人教版(必修5)(已下线)2019年10月13日 《每日一题》 必修5-每周一测江苏省淮安市盱眙县马坝高级中学2019-2020学年高二上学期期中数学试题江苏省苏州市陆慕高级中学2019-2020学年高二下学期在线学习质量检测数学试题江苏省徐州市铜山区大许中学2019-2020学年高二下学期期中数学试题江苏省徐州市丰县中学2019-2020学年高二下学期期中数学试题江苏省苏州市张家港市梁丰高级中学2020-2021学年高二上学期期中数学试题(已下线)5.3.2 函数的极值与最大(小)值(2)导学案河南省郑州市第七高级中学2020~2021学年高二上学期期中考试理科数学试题(已下线)专题12 导数在函数有关问题及实际生活中的应用 知识精讲 广东省佛山市顺德区罗定邦中学2020-2021学年高二下学期期中数学试题重庆市綦江中学2020-2021学年高二下学期第一次阶段性考试数学试题(已下线)6.3 利用导数解决实际问题(课后作业)-2020-2021学年高中数学同步备课学案(2019人教B版选择性必修第三册)(已下线)卷18 选择性必修第二册综合性测试卷 ·B卷·能力提升-【重难点突破】2021-2022学年高二数学名校好题汇编同步测试卷(人教A版选择性必修第二册) 河南省驻马店市2021-2022学年高二上学期期终考试文科数学试题河南省驻马店市2021-2022学年高二上学期期终考试理科数学试题北京市通州区2021-2022学年高二下学期期中质量检测数学试题福建省宁德市同心顺联盟2021-2022学年高二下学期期中联合考试数学试题四川省盐亭中学2021-2022学年高二下学期第四学月教学质量测试数学(文)试题江苏省南京市第二十七高级中学2022-2023学年高二上学期期末数学试题广东省深圳技术大学附属中学2022-2023学年高二下学期第一次月考数学试题安徽省皖北县中联盟2022-2023学年高二下学期3月联考数学试题陕西省渭南市韩城市新蕾中学2020-2021学年高二下学期第四次月考文科数学试题河北省邯郸市鸡泽县第一中学2022-2023学年高二下学期第一次月考数学试题(已下线)第5章导数及其应用(2) (A卷·知识通关练)安徽省庐巢七校联考2022-2023学年高二下学期3月期中数学试题(已下线)第五章 一元导数及其应用章末重点题型归纳(3)(已下线)拓展十二:导数大题的8种常见考法总结(2)山东省泰安市宁阳县第四中学2022-2023学年高二下学期6月月考数学试题(已下线)重难点04导数的应用六种解法(2)甘肃省天水市第一中学2022-2023学年高二下学期3月月考数学试题广东省深圳市人大附中深圳学校2022-2023学年高二下学期期中数学试题广东省深圳市第三高级中学2022-2023学年高二下学期期中数学试题人教A版(2019) 选修第二册 数学奇书 第五章 一元函数的导数及其应用 5.3.2 函数的极值与最大(小)值 第2课时 函数的最大(小)值【典例题】1.3.4 导数的应用举例 课堂例题-湘教版(2019)选择性必修第二册第1章 导数及其应用2010年普通高等学校招生全国统一考试(湖北卷)数学(理科)(已下线)2010年高考试题分项版理科数学之专题二 函数(已下线)2010年高考试题分项版理科数学之专题十三 导数(已下线)2011届江苏省宿豫中学高三第二次模拟考试数学试卷(已下线)2011届广东省华南师大附中高三综合测试数学文卷(已下线)2011届江西省鹰潭市高三第二次模拟考试理科数学卷(已下线)2012届山东省聊城莘县实验高中高三上学期期中考试数学(已下线)2012届上海市七宝中学高三模拟考试理科数学(已下线)2014届浙江省慈溪中学高三第一学期10月月考文科数学试卷(已下线)2014届陕西咸阳范公中学高三上学期摸底考试文科数学试卷(已下线)2015届河南省实验中学高三上学期期中考试文科数学试卷2015届上海市崇明县高三第二次高考模拟考试理科数学试卷2015届上海市崇明县高三第二次高考模拟考试文科数学试卷2014-2015学年江西省白鹭洲中学高一下学期期中考试数学试卷2015-2016学年湖北省广华中学高一9月阶段测试数学试卷2014-2015学年江西省余江县一中高一下学期期中数学试卷2016-2017学年江西吉安一中高一上段考一数学试卷2017届广东中山一中高三上学期统测二数学(文)试卷山东省平阴第二中学2016-2017高一下学期6月月调研卷数学(理)试题重庆市铜梁县第一中学2018届高三9月月考数学(理)试题高中数学人教版 必修5 第三章 不等式 3.4 基本不等式(已下线)学科网2019年高考数学一轮复习讲练测2.9函数模型及其应用【江苏版】【讲】(已下线)2019高考备考一轮复习精品资料 【理】专题十二 函数模型及其应用 教学案(已下线)2019高考热点题型和提分秘籍 【理数】专题9 函数模型及其应用( 题型专练)(已下线)2019高考热点题型和提分秘籍 【理数】专题9 函数模型及其应用( 教学案)(已下线)2019高考热点题型和提分秘籍 【文数】专题9 函数模型及其应用 (教学案)【全国百强校】上海市交通大学附属中学2017-2018学年高一上学期期末数学试题【全国百强校】广东省广州市第六中学2018-2019学年高一下学期期中数学试题(已下线)专题2.9 函数模型及其应用(讲)【文】-2020年高考一轮复习讲练测(已下线)专题2.9 函数模型及其应用(讲)【理】-《2020年高考一轮复习讲练测》山东省济南第一中学2017届高三10月阶段测试数学(文)试题安徽省黄山市屯溪第一中学2019-2020学年高一上学期10月月考数学试题上海市交通大学附属中学2018-2019学年高一下学期开学考试数学试题上海市上海交通大学附属中学2019-2020学年高一上学期期中数学试题上海市控江中学2018-2019学年高三上学期开学考试数学试题上海市曹杨第二中学2018-2019学年高一上学期期中数学试题上海市普陀区长征中学2018-2019学年高三上学期期中数学试题上海市南洋模范中学2017-2018学年高一上学期期中数学试题(已下线)专题15 以导数为背景的应用题-《巅峰冲刺2020年高考之二轮专项提升》(江苏)上海市行知中学2018届高三上学期期中数学试题2016届上海市高考最后冲刺模拟(一)(文)数学试题上海市曹杨二中2015-2016学年高一上学期期中数学试题上海市向明中学2016-2017学年高一上学期期中数学试题湖南省岳阳市第一中学2019-2020学年高一上学期期中数学试题(已下线)专题2.9 函数模型及其应用(精讲)-2021届高考数学(理)一轮复习讲练测(已下线)第12讲 函数与数学模型-2021年新高考数学一轮专题复习(新高考专版)(已下线)测试卷07 函数的应用-2021届高考数学一轮复习(文理通用)单元过关测试卷江苏省南通市四校(四星级学校)2020-2021学年高三上学期第一次联考数学试题上海市曹杨二中2020-2021学年高一上学期期中仿真密卷数学试题(已下线)【新东方】【2021.5.25】【NB】【高一上】【高中数学】【NB00100】上海市建平中学2022届高三上学期9月开学考试数学试题北师大版(2019) 选修第二册 名师精选 测试二 高考水平模拟性测试卷云南大学附属中学星耀学校2021-2022学年高一上学期期中考试数学试题江西省萍乡市芦溪中学2022届高三上学期第一次段考数学(理)试题湖北省2021-2022学年高一上学期期末调考数学试题江西省2021-2022学年高一上学期期末调研测试数学试题人教B版(2019) 选修第三册 名师精选 高考水平模拟性测试卷(已下线)复习题二2(已下线)第二章 一元二次函数、方程和不等式单元总结(思维导图+知识记诵+能力培养)-【一堂好课】2021-2022学年高一数学上学期同步精品课堂(人教A版2019必修第一册)湖南省岳阳市华容县第一中学2021-2022学年高一下学期开学考试数学试题(已下线)专题03 均值不等式及其应用(讲义)-2023年高考数学一轮复习精讲精练宝典(新高考专用)(已下线)3.3 函数的应用(一)(已下线)专题21 函数的应用(一)(1)上海市曹杨第二中学2022-2023学年高一上学期期中数学试题河北省保定市蠡县第二中学2022-2023学年高一上学期12月月考数学试题上海市文来高中2023届高三上学期期中数学试题河北省保定市第三中学2022-2023学年高一上学期期末数学试题3.4 函数的应用(一)(已下线)第2章 一元二次函数、方程和不等式(基础、典型、易错、新文化、压轴)分类专项训练湘教版(2019)必修第一册课本习题第2章复习题宁夏银川市第九中学2023-2024学年高一上学期第一次月考数学试题福建省莆田哲理中学2023-2024学年高一上学期10月月考数学试题广东省广州市番禺区洛溪新城中学2023-2024学年高一上学期10月月考数学试题海南省海口市观澜湖华侨学校2023-2024学年高一上学期10月月考数学试题甘肃省兰州市兰州第一中学2023-2024学年高三上学期期中数学试题湖南省衡阳市衡阳县2023-2024学年高一上学期1月期末质量检测数学试题上海市闵行(文琦)中学2023-2024学年高一下学期3月月考数学试卷
5 . 一投资者在两个投资方案中选择一个,这两个投资方案的利润X(万元)分别服从正态分布N(8,32)和N(7,12),投资者要求“利润超过5万元”的概率尽量大,那么他应该选择哪一个方案?
您最近一年使用:0次
2018-10-04更新
|
339次组卷
|
4卷引用:黑龙江省海林市朝鲜族中学人教版高中数学选修2-3同步练习:2.4 正态分布



