名校
1 . 定理(三角不等式),对于任意的 、
、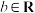 ,恒有
,恒有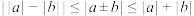 .定义:已知
.定义:已知 且
且 ,对于有序数组
,对于有序数组 、
、 、
、 、
、 ,称
,称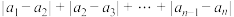 为有序数组
为有序数组 、
、 、
、 、
、 的波动距离,记作
的波动距离,记作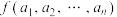 ,即
,即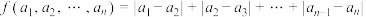 ,请根据上述俼息解决以下几个问题:
,请根据上述俼息解决以下几个问题:
(1)求函数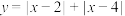 的最小值,并指出函数取到最小值时
的最小值,并指出函数取到最小值时 的取值范围;
的取值范围;
(2)①求有序数组 、
、 、
、 、
、 的波动距离
的波动距离 ;
;
②求证:若 、
、 、
、 、
、 且
且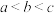 ,则
,则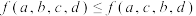 ;题(注:该命题无需证明,需要时可直接使用).设两两不相等的四个实数
;题(注:该命题无需证明,需要时可直接使用).设两两不相等的四个实数 、
、 、
、 、
、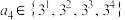 ,求有序数组
,求有序数组 、
、 、
、 、
、 的波动距离
的波动距离 的最大值.
的最大值.
 、
、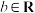 ,恒有
,恒有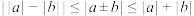 .定义:已知
.定义:已知 且
且 ,对于有序数组
,对于有序数组 、
、 、
、 、
、 ,称
,称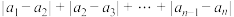 为有序数组
为有序数组 、
、 、
、 、
、 的波动距离,记作
的波动距离,记作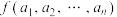 ,即
,即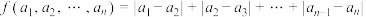 ,请根据上述俼息解决以下几个问题:
,请根据上述俼息解决以下几个问题:(1)求函数
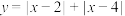 的最小值,并指出函数取到最小值时
的最小值,并指出函数取到最小值时 的取值范围;
的取值范围;(2)①求有序数组
 、
、 、
、 、
、 的波动距离
的波动距离 ;
;②求证:若
 、
、 、
、 、
、 且
且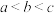 ,则
,则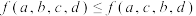 ;题(注:该命题无需证明,需要时可直接使用).设两两不相等的四个实数
;题(注:该命题无需证明,需要时可直接使用).设两两不相等的四个实数 、
、 、
、 、
、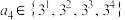 ,求有序数组
,求有序数组 、
、 、
、 、
、 的波动距离
的波动距离 的最大值.
的最大值.
您最近一年使用:0次
2022/08/22
|
559次组卷
|
7卷引用:上海市控江中学2021-2022学年高一上学期期中数学试题
上海市控江中学2021-2022学年高一上学期期中数学试题(已下线)专题02 等式与不等式(练习)-2上海市高桥中学2022-2023学年高一上学期期中数学试题(已下线)期中模拟预测卷03(测试范围:前三章)-2022-2023学年高一数学上学期期中期末考点大串讲(沪教版2020必修第一册)(已下线)上海高一上学期期中【压轴42题专练】(2)(已下线)第二章 等式与不等式(压轴题专练)-速记·巧练(沪教版2020必修第一册)上海市吴淞中学2023-2024学年高一上学期期中数学试题
2 . 已知任意二次曲线S, 是曲线S的弦,O是
是曲线S的弦,O是 的中点,过点O任意作弦
的中点,过点O任意作弦 、
、 ,过点C、D、E、F另作一条任意二次曲线t,如果曲线t与直线
,过点C、D、E、F另作一条任意二次曲线t,如果曲线t与直线 交于点P、Q,求证:
交于点P、Q,求证: .
.
 是曲线S的弦,O是
是曲线S的弦,O是 的中点,过点O任意作弦
的中点,过点O任意作弦 、
、 ,过点C、D、E、F另作一条任意二次曲线t,如果曲线t与直线
,过点C、D、E、F另作一条任意二次曲线t,如果曲线t与直线 交于点P、Q,求证:
交于点P、Q,求证: .
.
您最近一年使用:0次
真题
3 . 已知 ,数列
,数列 满足
满足 .
.
(1)已知数列 极限存在且大于零,求
极限存在且大于零,求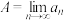 (将A用a表示);
(将A用a表示);
(2)设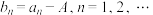 ,证明:
,证明: ;
;
(3)若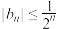 对
对 都成立,求a的取值范围.
都成立,求a的取值范围.
 ,数列
,数列 满足
满足 .
.(1)已知数列
 极限存在且大于零,求
极限存在且大于零,求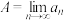 (将A用a表示);
(将A用a表示);(2)设
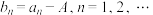 ,证明:
,证明: ;
;(3)若
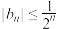 对
对 都成立,求a的取值范围.
都成立,求a的取值范围.
您最近一年使用:0次
解题方法
4 . 设动点 在直线
在直线 和
和 上的射影分别为点
上的射影分别为点 和
和 ,已知
,已知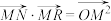 ,其中
,其中 为坐标原点.
为坐标原点.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)过直线 上的一点
上的一点 作轨迹
作轨迹 的两条切线
的两条切线 和
和 (
( ,
, 为切点),求证:直线
为切点),求证:直线 经过定点.
经过定点.
 在直线
在直线 和
和 上的射影分别为点
上的射影分别为点 和
和 ,已知
,已知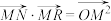 ,其中
,其中 为坐标原点.
为坐标原点.(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)过直线
 上的一点
上的一点 作轨迹
作轨迹 的两条切线
的两条切线 和
和 (
( ,
, 为切点),求证:直线
为切点),求证:直线 经过定点.
经过定点.
您最近一年使用:0次
5 . 已知椭圆 的焦距为2,O为坐标原点,F为右焦点,点
的焦距为2,O为坐标原点,F为右焦点,点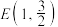 在椭圆上.
在椭圆上.
(1)求椭圆的标准方程;
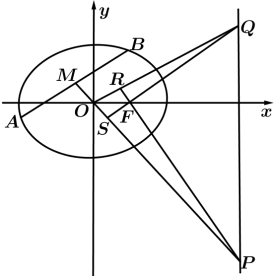
(2)若直线l的方程为 ,AB是椭圆上与坐标轴不平行的一条弦,M为弦的中点,直线MO交l于点P,过点O与AB平行的直线交/于点Q,直线PF交直线OQ于点R,直线QF交直线MO于点S.
,AB是椭圆上与坐标轴不平行的一条弦,M为弦的中点,直线MO交l于点P,过点O与AB平行的直线交/于点Q,直线PF交直线OQ于点R,直线QF交直线MO于点S.
①证明:O,S,F,R四点共圆;
②记△QRF的面积为 ,△QSO的面积为
,△QSO的面积为 ,求
,求 的取值范围.
的取值范围.
 的焦距为2,O为坐标原点,F为右焦点,点
的焦距为2,O为坐标原点,F为右焦点,点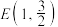 在椭圆上.
在椭圆上.
(1)求椭圆的标准方程;
(2)若直线l的方程为
 ,AB是椭圆上与坐标轴不平行的一条弦,M为弦的中点,直线MO交l于点P,过点O与AB平行的直线交/于点Q,直线PF交直线OQ于点R,直线QF交直线MO于点S.
,AB是椭圆上与坐标轴不平行的一条弦,M为弦的中点,直线MO交l于点P,过点O与AB平行的直线交/于点Q,直线PF交直线OQ于点R,直线QF交直线MO于点S.①证明:O,S,F,R四点共圆;
②记△QRF的面积为
 ,△QSO的面积为
,△QSO的面积为 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2021/11/13
|
1470次组卷
|
4卷引用:浙江省温州市环大罗山联盟2021-2022学年高二上学期期中联考数学试题
浙江省温州市环大罗山联盟2021-2022学年高二上学期期中联考数学试题浙江省“七彩阳光”新高考研究联盟2021-2022学年高二上学期期中联考数学试题 (已下线)第46讲 解析几何中的四点共圆问题-2022年新高考数学二轮专题突破精练(已下线)第五篇 向量与几何 专题10 圆锥曲线中的四点共圆问题 微点1 圆锥曲线中的四点共圆问题(一)
6 . 已知椭圆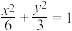 =1上有两点P(﹣2,1)及Q(2,﹣1),直线l:y=kx+b与椭圆交于A、B两点,与线段PQ交于点C(异于P、Q).
=1上有两点P(﹣2,1)及Q(2,﹣1),直线l:y=kx+b与椭圆交于A、B两点,与线段PQ交于点C(异于P、Q).
(1)当k=1且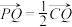 时,求直线l的方程;
时,求直线l的方程;
(2)当k=2时,求四边形PAQB面积的取值范围;
(3)记直线PA、PB、QA、QB的斜率依次为k1、k2、k3、k4.当b≠0且线段AB的中点M在直线y=﹣x上时,计算k1⋅k2的值,并证明:k12+k22>2k3k4.
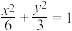 =1上有两点P(﹣2,1)及Q(2,﹣1),直线l:y=kx+b与椭圆交于A、B两点,与线段PQ交于点C(异于P、Q).
=1上有两点P(﹣2,1)及Q(2,﹣1),直线l:y=kx+b与椭圆交于A、B两点,与线段PQ交于点C(异于P、Q).(1)当k=1且
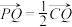 时,求直线l的方程;
时,求直线l的方程;(2)当k=2时,求四边形PAQB面积的取值范围;
(3)记直线PA、PB、QA、QB的斜率依次为k1、k2、k3、k4.当b≠0且线段AB的中点M在直线y=﹣x上时,计算k1⋅k2的值,并证明:k12+k22>2k3k4.
您最近一年使用:0次
名校
解题方法
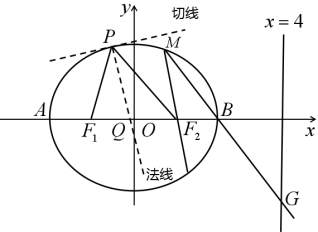
7 . 如图,椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.已知椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 ,
, ,左、右顶点分别为
,左、右顶点分别为 ,
, ,一光线从点
,一光线从点 射出经椭圆
射出经椭圆 上
上 点反射,法线(与椭圆
点反射,法线(与椭圆 在
在 处的切线垂直的直线)与
处的切线垂直的直线)与 轴交于点
轴交于点 ,已知
,已知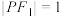 ,
,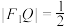 .
.
(1)求椭圆 的方程.
的方程.
(2)过 的直线与椭圆
的直线与椭圆 交于
交于 ,
, 两点(均不与
两点(均不与 ,
, 重合),直线
重合),直线 与直线
与直线 交于
交于 点,证明:
点,证明: ,
, ,
, 三点共线.
三点共线.
 :
: 的左、右焦点分别为
的左、右焦点分别为 ,
, ,左、右顶点分别为
,左、右顶点分别为 ,
, ,一光线从点
,一光线从点 射出经椭圆
射出经椭圆 上
上 点反射,法线(与椭圆
点反射,法线(与椭圆 在
在 处的切线垂直的直线)与
处的切线垂直的直线)与 轴交于点
轴交于点 ,已知
,已知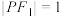 ,
,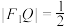 .
.
(1)求椭圆
 的方程.
的方程.(2)过
 的直线与椭圆
的直线与椭圆 交于
交于 ,
, 两点(均不与
两点(均不与 ,
, 重合),直线
重合),直线 与直线
与直线 交于
交于 点,证明:
点,证明: ,
, ,
, 三点共线.
三点共线.
您最近一年使用:0次
2021/05/01
|
658次组卷
|
4卷引用:湖南省2021届高三下学期4月联考数学试题



