1 . 已知集合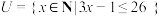 ,
,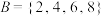 ,
,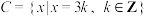 .
.
(1)用列举法表示集合U;
(2)求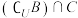 .
.
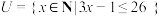 ,
,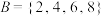 ,
,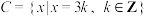 .
.(1)用列举法表示集合U;
(2)求
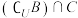 .
.
您最近一年使用:0次
名校
解题方法
2 . 设集合A为非空数集,定义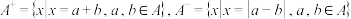 .
.
(1)若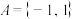 ,写出集合
,写出集合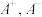 ;
;
(2)若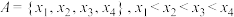 ,且
,且 ,求证:
,求证: ;
;
(3)若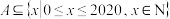 ,且
,且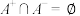 ,求集合A元素个数的最大值.
,求集合A元素个数的最大值.
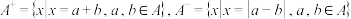 .
.(1)若
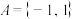 ,写出集合
,写出集合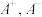 ;
;(2)若
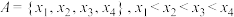 ,且
,且 ,求证:
,求证: ;
;(3)若
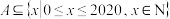 ,且
,且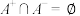 ,求集合A元素个数的最大值.
,求集合A元素个数的最大值.
您最近一年使用:0次
3 . 下列关于集合相等的说法正确的有( )
①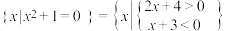 ;
;
② ;
;
③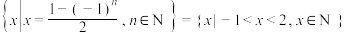 ;
;
④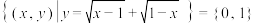
①
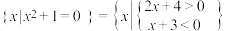 ;
;②
 ;
;③
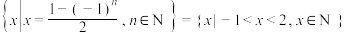 ;
;④
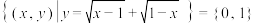
| A.0个 | B.1个 | C.2个 | D.3个 |
您最近一年使用:0次
名校
4 . 已知集合 满足
满足 ,那么这样的集合M的个数为( )
,那么这样的集合M的个数为( )
 满足
满足 ,那么这样的集合M的个数为( )
,那么这样的集合M的个数为( )| A.6 | B.7 | C.8 | D.9 |
您最近一年使用:0次
2023-03-07更新
|
4106次组卷
|
13卷引用:辽宁省沈阳市五校协作体2022-2023学年高一上学期期末数学试题
辽宁省沈阳市五校协作体2022-2023学年高一上学期期末数学试题(已下线)第一章 集合与常用逻辑用语 讲核心(已下线)1.2 子集、全集、补集-【题型分类归纳】(苏教版2019必修第一册)(已下线)1.2集合间的基本关系(分层作业)-【上好课】(已下线)1.2 集合间的基本关系(5大题型)精讲-【题型分类归纳】(已下线)1.1.2 集合的基本关系(分层练习)-高一数学同步精品课堂(人教B版2019必修第一册)四川省眉山市彭山区第一中学2023-2024学年高一上学期入学考试数学试题(已下线)第一章 集合与常用逻辑用语(知识归纳+7类题型突破)-速记·巧练(人教A版2019必修第一册)(已下线)专题02集合间的基本关系1-【倍速学习法】(人教A版2019必修第一册)(已下线)1.2集合间的基本关系【第二练】江西省赣州市宁都中学2024-2025学年8月高一上学期开学考试数学试题浙江省金华十校2022-2023学年高三下学期4月模拟考试预演数学试题(已下线)1.1 集合-2
名校
5 . 设集合 .
.
(1)用列举法表示集合 ;
;
(2)若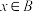 是
是 的必要条件,求实数
的必要条件,求实数 的值.
的值.
 .
.(1)用列举法表示集合
 ;
;(2)若
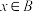 是
是 的必要条件,求实数
的必要条件,求实数 的值.
的值.
您最近一年使用:0次
2022-11-26更新
|
493次组卷
|
6卷引用:辽宁省朝阳市建平县实验中学2022-2023学年高一上学期期中数学试题
6 . 已知全集 ,集合
,集合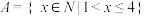 ,
,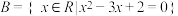
(1)用列举法表示集合 与
与 ;
;
(2)求 及
及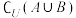 .
.
 ,集合
,集合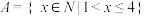 ,
,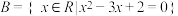
(1)用列举法表示集合
 与
与 ;
;(2)求
 及
及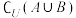 .
.
您最近一年使用:0次
2021-11-20更新
|
577次组卷
|
9卷引用:辽宁省沈阳市辽中区第二高级中学2022-2023学年高一上学期期中考试数学试题
辽宁省沈阳市辽中区第二高级中学2022-2023学年高一上学期期中考试数学试题辽宁省重点高中沈阳市郊联体2022-2023学年高一上学期期中数学试题北京市海淀区北京医学院附属中学2021-2022学年高一10月月考数学试题湖北省黄冈市黄梅国际育才高级中学2022-2023学年高一上学期期中数学试题第一章 预备知识 单元测试-2022-2023学年高一上学期数学北师大版(2019)必修第一册(已下线)1.3全集与补集(第2课时)(导学案)-【上好课】(已下线)1.3全集与补集 (第2课时)(分层作业)-【上好课】(已下线)期中真题必刷压轴60题(15个考点专练)-【满分全攻略】(人教A版2019必修第一册)新疆维吾尔自治区喀什地区莎车县2024-2025学年高一上学期期中考试数学试题
名校
7 . 对正整数 ,记
,记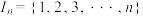 ,
,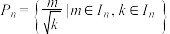 .
.
(1)用列举法表示集合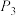 ;
;
(2)求集合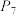 中元素的个数;
中元素的个数;
(3)若 的子集
的子集 中任意两个元素之和不是整数的平方,则称
中任意两个元素之和不是整数的平方,则称 为“稀疏集”.证明:存在
为“稀疏集”.证明:存在 使得
使得 能分成两个不相交的稀疏集的并集,且
能分成两个不相交的稀疏集的并集,且 的最大值为14.
的最大值为14.
 ,记
,记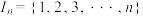 ,
,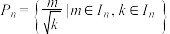 .
.(1)用列举法表示集合
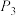 ;
;(2)求集合
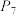 中元素的个数;
中元素的个数;(3)若
 的子集
的子集 中任意两个元素之和不是整数的平方,则称
中任意两个元素之和不是整数的平方,则称 为“稀疏集”.证明:存在
为“稀疏集”.证明:存在 使得
使得 能分成两个不相交的稀疏集的并集,且
能分成两个不相交的稀疏集的并集,且 的最大值为14.
的最大值为14.
您最近一年使用:0次
2021-10-17更新
|
1160次组卷
|
8卷引用:辽宁省大连市育明高级中学2024-2025学年高一上学期10月月考数学试卷
辽宁省大连市育明高级中学2024-2025学年高一上学期10月月考数学试卷上海市大同中学2021-2022学年高一上学期10月月考数学试题(已下线)1.1 集合的运算(第4课时)上海市青浦高级中学2022-2023学年高一上学期期中数学试题(已下线)第1章 集合与逻辑(基础、典型、新文化、压轴)分类专项训练-2022-2023学年高一数学考试满分全攻略(沪教版2020必修第一册)湖南省岳阳市2022-2023学年高一下学期期中数学试题(已下线)难关必刷01集合的综合问题(3种题型30题专项训练)-【满分全攻略】(沪教版2020必修第一册)(已下线)高一上学期第一次月考13大压轴考法60题(第1~2章:集合与逻辑+等式与不等式)-【常考压轴题】(沪教版2020必修第一册)



