名校
解题方法
1 . 某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现注意力指数p与听课时间t之间的关系满足如图所示的曲线.当 时,曲线是二次函数图象的一部分,当
时,曲线是二次函数图象的一部分,当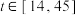 时,曲线是函数
时,曲线是函数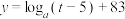 (
( 且
且 )图象的一部分.根据专家研究,当注意力指数p大于80时听课效果最佳.
)图象的一部分.根据专家研究,当注意力指数p大于80时听课效果最佳.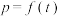 的函数关系式;
的函数关系式;
(2)老师在什么时段内讲解核心内容能使学生听课效果最佳?请说明理由.
 时,曲线是二次函数图象的一部分,当
时,曲线是二次函数图象的一部分,当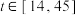 时,曲线是函数
时,曲线是函数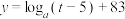 (
( 且
且 )图象的一部分.根据专家研究,当注意力指数p大于80时听课效果最佳.
)图象的一部分.根据专家研究,当注意力指数p大于80时听课效果最佳.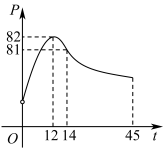
 的函数关系式;
的函数关系式;(2)老师在什么时段内讲解核心内容能使学生听课效果最佳?请说明理由.
您最近一年使用:0次
2023-07-12更新
|
732次组卷
|
5卷引用:第四章幂函数、指数函数和对数函数单元测试
名校
解题方法
2 . 已知二次函数 满足
满足 ,请从下列①和②两个条件中选一个作为已知条件,完成下面问题.
,请从下列①和②两个条件中选一个作为已知条件,完成下面问题.
①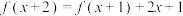 ;②不等式
;②不等式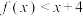 的解集为
的解集为 .
.
(1)求 的解析式;
的解析式;
(2)若 在
在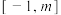 上的值域为
上的值域为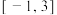 ,求实数
,求实数 的取值范围.
的取值范围.
 满足
满足 ,请从下列①和②两个条件中选一个作为已知条件,完成下面问题.
,请从下列①和②两个条件中选一个作为已知条件,完成下面问题.①
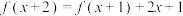 ;②不等式
;②不等式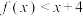 的解集为
的解集为 .
.(1)求
 的解析式;
的解析式;(2)若
 在
在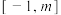 上的值域为
上的值域为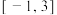 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-02-19更新
|
678次组卷
|
5卷引用:江西省萍乡市2022-2023学年高一上学期期末考试数学试题
江西省萍乡市2022-2023学年高一上学期期末考试数学试题黑龙江省齐齐哈尔市第六中学校2023-2024学年高一上学期9月月考数学试题(已下线)模块六 专题4 全真能力模拟2(已下线)高一上学期期末复习【第二章 一元二次函数、方程和不等式】(基础篇)-举一反三系列(江西省多校2024-2025学年高一上学期阶段测试(二)(10月)数学试题
名校
解题方法
3 . 已知函数 的定义域为
的定义域为 ,
,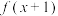 为奇函数,
为奇函数,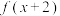 为偶函数,当
为偶函数,当 时,
时, .若
.若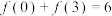 ,则
,则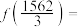 ( )
( )
 的定义域为
的定义域为 ,
,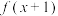 为奇函数,
为奇函数,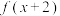 为偶函数,当
为偶函数,当 时,
时, .若
.若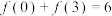 ,则
,则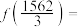 ( )
( )A. | B.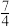 | C.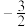 | D.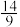 |
您最近一年使用:0次
名校
解题方法
4 . 已知函数 ,二次函数
,二次函数 满足:
满足: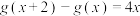 且
且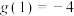 .
.
(1)求 的解析式;
的解析式;
(2)若 ,解关于
,解关于 的不等式
的不等式 .
.
 ,二次函数
,二次函数 满足:
满足: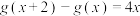 且
且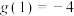 .
.(1)求
 的解析式;
的解析式;(2)若
 ,解关于
,解关于 的不等式
的不等式 .
.
您最近一年使用:0次
名校
解题方法
5 . 某商店购进一批成本为每件30元的商品,经调查发现,该商品每天的销售量 (件)与销售单价
(件)与销售单价 (元)之间满足一次函数关系,其图象如图所示.
(元)之间满足一次函数关系,其图象如图所示. 与销售单价
与销售单价 之间的函数关系式;
之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于50元销售,则销售单价定为多少元时利润最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于800元,则每天的销售量最少应为多少件?
 (件)与销售单价
(件)与销售单价 (元)之间满足一次函数关系,其图象如图所示.
(元)之间满足一次函数关系,其图象如图所示.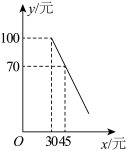
 与销售单价
与销售单价 之间的函数关系式;
之间的函数关系式;(2)若商店按单价不低于成本价,且不高于50元销售,则销售单价定为多少元时利润最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于800元,则每天的销售量最少应为多少件?
您最近一年使用:0次
2024-09-06更新
|
463次组卷
|
4卷引用:河北省石家庄市河北灵寿中学2024-2025学年高一上学期开学考试数学试题
河北省石家庄市河北灵寿中学2024-2025学年高一上学期开学考试数学试题(已下线)专题2 函数解析式与值域的求法【讲】(高一期中压轴专项)解答题湖南省衡阳市衡阳县第四中学2024-2025学年高一上学期10月月考数学试题广东省江门市鹤山市广旭实验学校2024-2025学年高一上学期第一次月考数学试题
名校
解题方法
6 . 已知二次函数 最小值为
最小值为 ,且
,且 是其一个零点,
是其一个零点,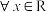 都有
都有 .
.
(1)求 的解析式;
的解析式;
(2)求 在区间
在区间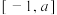 上的最小值;
上的最小值;
(3)是否存在实数 满足:对
满足:对 ,都有
,都有 恒成立?若存在,求实数
恒成立?若存在,求实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
 最小值为
最小值为 ,且
,且 是其一个零点,
是其一个零点,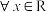 都有
都有 .
.(1)求
 的解析式;
的解析式;(2)求
 在区间
在区间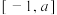 上的最小值;
上的最小值;(3)是否存在实数
 满足:对
满足:对 ,都有
,都有 恒成立?若存在,求实数
恒成立?若存在,求实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
您最近一年使用:0次
2023-11-05更新
|
520次组卷
|
2卷引用:北京市清华大学附属中学2023-2024学年高一上学期期中考试数学试题
名校
解题方法
7 . 已知函数 定义域为
定义域为 ,
, 为奇函数,
为奇函数, 为偶函数,当
为偶函数,当 时,
时,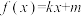 ,若
,若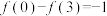 ,则
,则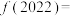 ( )
( )
 定义域为
定义域为 ,
, 为奇函数,
为奇函数, 为偶函数,当
为偶函数,当 时,
时,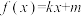 ,若
,若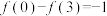 ,则
,则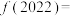 ( )
( )A. | B.1 | C.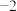 | D.2 |
您最近一年使用:0次
2022-10-25更新
|
855次组卷
|
2卷引用:黑龙江省哈尔滨市第六中学校2022-2023学年高三上学期10月月考数学试题
解题方法
8 . 二次函数 满足
满足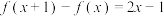 ,且
,且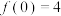 .
.
(1)求 的解析式;
的解析式;
(2)若 时,
时, 的图象恒在
的图象恒在 图象的上方,试确定实数
图象的上方,试确定实数 的取值范围.
的取值范围.
 满足
满足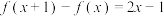 ,且
,且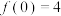 .
.(1)求
 的解析式;
的解析式;(2)若
 时,
时, 的图象恒在
的图象恒在 图象的上方,试确定实数
图象的上方,试确定实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
9 . 已知函数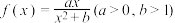 满足
满足 ,且
,且 在
在 上有最大值
上有最大值 .
.
(1)求 ,
, 的值;
的值;
(2)当 时,不等式
时,不等式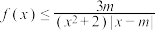 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
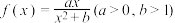 满足
满足 ,且
,且 在
在 上有最大值
上有最大值 .
.(1)求
 ,
, 的值;
的值;(2)当
 时,不等式
时,不等式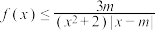 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
10 . 已知二次函数 同时满足以下条件:①
同时满足以下条件:① ,②
,② ,③
,③ .
.
(1)求函数 的解析式;
的解析式;
(2)若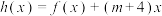 ,
, ,求
,求 的最小值
的最小值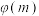 ;
;
 同时满足以下条件:①
同时满足以下条件:① ,②
,② ,③
,③ .
.(1)求函数
 的解析式;
的解析式;(2)若
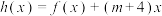 ,
, ,求
,求 的最小值
的最小值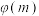 ;
;
您最近一年使用:0次



