1 . 某工厂对员工的计件工资标准进行改革,现制订了 ,
, 两种计件工资核算方案,员工的计件工资
两种计件工资核算方案,员工的计件工资 (单位:千元)与其生产的产品件数
(单位:千元)与其生产的产品件数 (单位:百件)的函数关系如图所示,则下列结论正确的是( )
(单位:百件)的函数关系如图所示,则下列结论正确的是( )
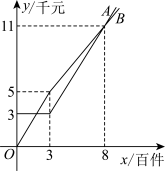
 ,
, 两种计件工资核算方案,员工的计件工资
两种计件工资核算方案,员工的计件工资 (单位:千元)与其生产的产品件数
(单位:千元)与其生产的产品件数 (单位:百件)的函数关系如图所示,则下列结论正确的是( )
(单位:百件)的函数关系如图所示,则下列结论正确的是( )
A.当某员工生产的产品件数为800时,该员工采用 , , 方案核算的计件工资相同 方案核算的计件工资相同 |
B.当某员工生产的产品件数为500时,该员工采用 方案核算的计件工资更多 方案核算的计件工资更多 |
C.当某员工生产的产品件数为200时,该员工采用 方案核算的计件工资更多 方案核算的计件工资更多 |
| D.当某员工生产的产品件数为1000时,该员工的计件工资最多为14200元 |
您最近一年使用:0次
名校
2 . 某打车平台欲对收费标准进行改革,现制定了甲、乙两种方案供乘客选择,其支付费用与打车里程数的函数关系大致如图所示,则下列说法正确的是( )
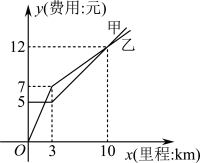

A.当打车距离为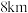 时,乘客选择乙方案省钱 时,乘客选择乙方案省钱 |
B.当打车距离为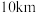 时,乘客选择甲、乙方案均可 时,乘客选择甲、乙方案均可 |
C.打车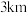 以上时,每公里增加的费用甲方案比乙方案多 以上时,每公里增加的费用甲方案比乙方案多 |
D.甲方案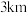 内(含 内(含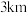 )付费5元,行程大于 )付费5元,行程大于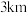 每增加1公里费用增加0.7元 每增加1公里费用增加0.7元 |
您最近一年使用:0次
2023-09-06更新
|
397次组卷
|
15卷引用:广西钦州市2021-2022学年高一上学期期末考试数学试题
广西钦州市2021-2022学年高一上学期期末考试数学试题山东省烟台市招远第一中学2021-2022学年高一上学期期中数学试题北师大版(2019) 必修第一册 名校名师卷 第五单元 生活中的变量关系、函数2023版 苏教版(2019) 必修第一册 名校名师卷 第六单元 函数的概念和图象、函数的表示方法2023版 湘教版(2019) 必修第一册 突围者 第3章 全章综合检测苏教版(2019) 必修第一册 突围者 第5章 全章综合检测2023版 湘教版(2019) 必修第一册 名师精选卷 第五单元 函数的概念、函数的表示法浙江省杭州市临安中学2022-2023学年高一上学期期中模拟数学试题云南省大理下关第一中学教育集团2022-2023学年高一上学期期中考试数学试题人教A版(2019) 必修第一册 数学奇书 学业评价(十七) 函数的表示法江苏省南通市海安市实验中学2022-2023学年高一上学期12月月考数学试题(已下线)4.5 函数的应用(二)(精讲)-《一隅三反》(已下线)3.4 函数的应用(一)(6大题型)精讲-【题型分类归纳】(人教A版2019必修第一册)河北省邢台市临西县翰林中学2023-2024学年高一上学期期中数学试题(已下线)模块二 专题2《函数的应用》单元检测篇 A基础卷 (人教A)
3 . 依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得法》向国家缴纳个人所得税(简称个税).一般地,个税税额的计算方式有两种:
方式一:分级累积计算税额.计算公式:个税税额=应纳税所得额×税率;
方式二:快速计算税额.计算公式:个税税额=应纳税所得额×税率-速算扣除数.
假定:应纳税所得额=税前收入-免征额.其中,免征额为每年60000元.
下表为个人所得税率表(2019年1月1日起执行)
下列说法正确的是( )
方式一:分级累积计算税额.计算公式:个税税额=应纳税所得额×税率;
方式二:快速计算税额.计算公式:个税税额=应纳税所得额×税率-速算扣除数.
假定:应纳税所得额=税前收入-免征额.其中,免征额为每年60000元.
下表为个人所得税率表(2019年1月1日起执行)
| 级数 | 全年应纳税所得额所在区间 | 税率(%) | 速算扣除数 |
| 1 |  | 3 | 0 |
| 2 | 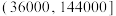 | 10 | 2520 |
| 3 |  | 20 | 16920 |
| 4 | 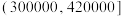 | 25 | X |
| 5 | 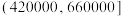 | 30 | 52920 |
| 6 | 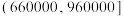 | 35 | 85920 |
| 7 | 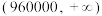 | 45 | 181920 |
| A.若小李2021年全年应纳税所得额为30000元,则小李应缴纳个税税额为900元 |
| B.若小林2021年全年应缴纳个税税额为7480元,则小林全年税前收入为160000元 |
C.按个税计算办法,表中的数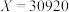 |
| D.若小华2021年税后所得为200000元,则他的全年应纳税所得额为153850元 |
您最近一年使用:0次
4 . 某城市有一个面积为1 的矩形广场,该广场为黄金矩形(它的宽与长的比为
的矩形广场,该广场为黄金矩形(它的宽与长的比为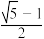 ),在中央设计一个矩形草坪,四周是等宽的步行道,能否设计恰当的步行道宽度使矩形草坪为黄金矩形?下列选项不正确的是( )
),在中央设计一个矩形草坪,四周是等宽的步行道,能否设计恰当的步行道宽度使矩形草坪为黄金矩形?下列选项不正确的是( )
 的矩形广场,该广场为黄金矩形(它的宽与长的比为
的矩形广场,该广场为黄金矩形(它的宽与长的比为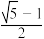 ),在中央设计一个矩形草坪,四周是等宽的步行道,能否设计恰当的步行道宽度使矩形草坪为黄金矩形?下列选项不正确的是( )
),在中央设计一个矩形草坪,四周是等宽的步行道,能否设计恰当的步行道宽度使矩形草坪为黄金矩形?下列选项不正确的是( )A.步行道的宽度为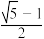 m m | B.步行道的宽度为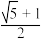 m m |
| C.步行道的宽度为5m | D.草坪不可能为黄金矩形 |
您最近一年使用:0次
2022-12-29更新
|
221次组卷
|
2卷引用:湖北省十堰市2022-2023学年高一上学期期末数学试题
名校
5 . 几名大学生创业时经过调研选择了一种技术产品,生产此产品获得的月利润 (单位:万元)与每月投入的研发经费
(单位:万元)与每月投入的研发经费 (单位:万元)有关.已知每月投入的研发经费不高于16万元,且
(单位:万元)有关.已知每月投入的研发经费不高于16万元,且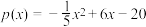 ,利润率
,利润率 .现在已投入研发经费9万元,则下列判断正确的是( )
.现在已投入研发经费9万元,则下列判断正确的是( )
 (单位:万元)与每月投入的研发经费
(单位:万元)与每月投入的研发经费 (单位:万元)有关.已知每月投入的研发经费不高于16万元,且
(单位:万元)有关.已知每月投入的研发经费不高于16万元,且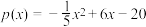 ,利润率
,利润率 .现在已投入研发经费9万元,则下列判断正确的是( )
.现在已投入研发经费9万元,则下列判断正确的是( )| A.此时获得最大利润率 | B.再投入6万元研发经费才能获得最大利润 |
| C.再投入1万元研发经费可获得最大利润率 | D.再投入1万元研发经费才能获得最大利润 |
您最近一年使用:0次
2022-08-17更新
|
1538次组卷
|
17卷引用:山西省2020-2021学年高一上学期期末数学试题
山西省2020-2021学年高一上学期期末数学试题(已下线)专题04 函数的性质与应用1-期末复习重难培优与单元检测(人教A版2019)新疆乌鲁木齐市新疆实验中学2022-2023学年高一上学期期末考试数学试卷广东省深圳市2021-2022学年高二下学期期末联考模拟一数学试题河北省曲阳县第一高级中学2021-2022学年高二下学期期末模拟数学试题苏教版(2019) 必修第一册 突围者 第8章 第二节 课时2 函数的实际应用江苏省盐城市射阳中学2022-2023学年高一上学期第一次月考数学试题宁夏石嘴山市平罗中学2022-2023学年高一上学期11月期中考试数学试题(已下线)第19讲 函数模型的应用-【暑假自学课】(人教A版2019必修第一册)(已下线)3.4 函数的应用(一)(重难点突破)-【冲刺满分】(已下线)专题3.7 函数的概念与性质全章综合测试卷(基础篇)-举一反三系列3.4 函数的应用(一)练习(已下线)3.4 函数的应用(一)-高一数学同步精品课堂(人教A版2019必修第一册)(已下线)专题12函数的应用(一)-【倍速学习法】(已下线)3.4函数的应用(一)【第三课】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)专题03 函数的概念与性质1-2024年高一数学寒假作业单元合订本(已下线)FHsx1225yl033
2023高三·全国·专题练习
名校
6 . (多选)甲同学家到乙同学家的途中有一座公园,甲同学家到公园的距离与乙同学家到公园的距离都是2 km.如图所示表示甲同学从家出发到乙同学家经过的路程y(km)与时间x(min)的关系,下列结论正确的是( )
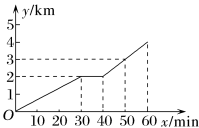

| A.甲同学从家出发到乙同学家走了60 min |
| B.甲从家到公园的时间是30 min |
| C.甲从家到公园的速度比从公园到乙同学家的速度快 |
D.当0≤x≤30时,y与x的关系式为y= x x |
您最近一年使用:0次
2022-07-17更新
|
1146次组卷
|
14卷引用:新疆阿勒泰地区2023-2024学年高一上学期期末联考数学试题
新疆阿勒泰地区2023-2024学年高一上学期期末联考数学试题(已下线)突破3.4 函数的应用(一)(重难点突破)陕西省咸阳市武功县2022-2023学年高一上学期期中数学试题广东省广州市十六中2022-2023学年高一上学期期中数学试题广东省普宁市勤建学校2022-2023学年高一上学期期中数学试题第五章 函数的应用(综合检测卷)-2022-2023学年高一数学北师大版2019必修第一册湖北省华科附中等五校联考体2020-2021学年高一上学期期中联考数学试题(已下线)第三章 函数的概念与性质单元测试(基础版)-【冲刺满分】(已下线)3.4 函数的应用(一)(重难点突破)-【冲刺满分】(已下线)第06讲 函数的应用(一)-【帮课堂】(人教A版2019必修第一册)湖南省长沙市长郡中学2022-2023学年高一上学期期中复习数学试题(已下线)4.5.3 函数模型的应用(导学案)-【上好课】(已下线)4.5.3 函数模型的应用(分层作业)-【上好课】(已下线)第18讲 函数模型及其运用-备战2023年高考数学一轮复习考点帮(新高考专用)
名校
7 . 边际函数是经济学中一个基本概念,在国防、医学、环保和经济管理等许多领域都有十分广泛的应用,函数 的边际函数
的边际函数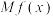 定义为
定义为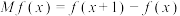 .某公司每月最多生产75台报警系统装置,生产
.某公司每月最多生产75台报警系统装置,生产 台
台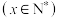 的收入函数
的收入函数 (单位:元),其成本的数
(单位:元),其成本的数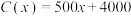 (单位:元),利润是收入与成本之差,设利润函数为
(单位:元),利润是收入与成本之差,设利润函数为 ,则以下说法正确的是( )
,则以下说法正确的是( )
 的边际函数
的边际函数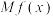 定义为
定义为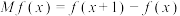 .某公司每月最多生产75台报警系统装置,生产
.某公司每月最多生产75台报警系统装置,生产 台
台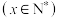 的收入函数
的收入函数 (单位:元),其成本的数
(单位:元),其成本的数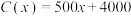 (单位:元),利润是收入与成本之差,设利润函数为
(单位:元),利润是收入与成本之差,设利润函数为 ,则以下说法正确的是( )
,则以下说法正确的是( )A. 取得最大值时每月产量为 取得最大值时每月产量为 台 台 |
B.边际利润函数的表达式为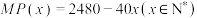 |
C.利润函数 与边际利润函数 与边际利润函数 不具有相同的最大值 不具有相同的最大值 |
D.边际利润函数 说明随着产量的增加,每台利润与前一台利润差额在减少 说明随着产量的增加,每台利润与前一台利润差额在减少 |
您最近一年使用:0次
2022-02-21更新
|
793次组卷
|
6卷引用:福建省福州市2021-2022学年高一上学期期末质量抽测数学试题
福建省福州市2021-2022学年高一上学期期末质量抽测数学试题山东省临沂市临沂第一中学2022-2023学年高一上学期期末数学试题(已下线)专题3.8 函数的应用(一)-重难点题型检测-2022-2023学年高一数学举一反三系列(人教A版2019必修第一册)(已下线)4.5.3 函数模型的应用(导学案)-【上好课】(已下线)4.5.3 函数模型的应用(分层作业)-【上好课】(已下线)专题07函数模型-2022年新高三数学暑假自学课精讲精练
8 . (多选)某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系t=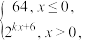 且该食品在4 ℃的保鲜时间是16小时.已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时刻的变化如图所示,则下列结论中正确的是( )
且该食品在4 ℃的保鲜时间是16小时.已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时刻的变化如图所示,则下列结论中正确的是( )

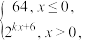 且该食品在4 ℃的保鲜时间是16小时.已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时刻的变化如图所示,则下列结论中正确的是( )
且该食品在4 ℃的保鲜时间是16小时.已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时刻的变化如图所示,则下列结论中正确的是( )
| A.该食品在6 ℃的保鲜时间是8小时 |
| B.当x∈[-6,6]时,该食品的保鲜时间t随着x的增大而逐渐减少 |
| C.到了此日13时,甲所购买的食品还在保鲜时间内 |
| D.到了此日14时,甲所购买的食品已然过了保鲜时间 |
您最近一年使用:0次
2021-12-10更新
|
934次组卷
|
5卷引用:内蒙古自治区通辽市开鲁县第一中学2022-2023学年高一上学期期末数学试题
内蒙古自治区通辽市开鲁县第一中学2022-2023学年高一上学期期末数学试题(已下线)专题05 与指数函数相关的情景化试题 - 2021-2022学年高一数学新教材情境化新题(人教A版2019必修第一册)苏教版(2019) 必修第一册 突围者 第8章 第二节 课时2 函数的实际应用江苏省镇江市扬中市第二高级中学2022-2023学年高三上学期期初检测数学试题(已下线)第二章 函数的概念与性质 第七节 指数函数(A素养养成卷)
名校
解题方法
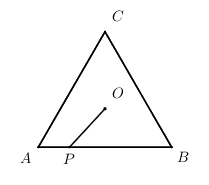
9 . 如图,在等边三角形 中,
中, .动点
.动点 从点
从点 出发,沿着此三角形三边逆时针运动回到
出发,沿着此三角形三边逆时针运动回到 点,记
点,记 运动的路程为
运动的路程为 ,点
,点 到此三角形中心
到此三角形中心 距离的平方为
距离的平方为 ,给出下列结论正确的有( )
,给出下列结论正确的有( )
 中,
中, .动点
.动点 从点
从点 出发,沿着此三角形三边逆时针运动回到
出发,沿着此三角形三边逆时针运动回到 点,记
点,记 运动的路程为
运动的路程为 ,点
,点 到此三角形中心
到此三角形中心 距离的平方为
距离的平方为 ,给出下列结论正确的有( )
,给出下列结论正确的有( )
A.函数 的最大值为12; 的最大值为12; |
B.函数 的最小值为6; 的最小值为6; |
C.关于 的方程 的方程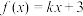 最多有6个实数根; 最多有6个实数根; |
D.当 时 时 能取得最大值. 能取得最大值. |
您最近一年使用:0次
2021-10-23更新
|
331次组卷
|
2卷引用:云南省昆明市西山区2022-2023学年高一上学期2月期末考试数学试题
10 . 某商品A以每件2元的价格出售时,销售量为10万件.经过调查,单价每提高0.2元,销售量减少5000件,要使商品A销售总收入不少于22.4万元,该商品A的单价可定为( )
| A.2.6元 | B.2.8元 | C.3元 | D.3.2元 |
您最近一年使用:0次
2021-08-09更新
|
1743次组卷
|
10卷引用:浙江省衢州市2020-2021学年高一下学期期末数学试题
浙江省衢州市2020-2021学年高一下学期期末数学试题(已下线)期末测试卷01(B卷·提升能力)-2021-2022学年高一数学同步单元AB卷(苏教版2019必修第一册)【学科网名师堂】(已下线)专题02 与一元二次函数、不等式和方程相关的情景化试题 - 2021-2022学年高一数学新教材情境化新题(人教A版2019必修第一册) (已下线)专题3.8 函数的应用(一)-重难点题型检测-2021-2022学年高一数学举一反三系列(人教A版2019必修第一册)(已下线)专题25. 3.5 函数的应用(1)- 2021-2022高一上学期数学新教材配套提升训练(人教B版2019必修一)(已下线)3.4函数的应用(一)B卷(已下线)突破3.4 函数的应用(一)(课时训练)内蒙古自治区阿拉善盟阿拉善右旗第一中学2022-2023学年高一上学期期中数学试题(已下线)3.4 函数的应用(一)(AB分层训练)-【冲刺满分】(已下线)3.4函数的应用(一)(导学案)-【上好课】



