1 . 如图,河对岸有两棵树A、B,由于缺少渡河工具,无法过河直接测得A、B之间的距离.假定可测得从本岸上的任意一点出发的两条射线之间的夹角,以及本岸上任意两点之间的距离,请你利用解斜三角形的方法,设计测量 距离的方案,并给出具体的计算方法.
距离的方案,并给出具体的计算方法.
 距离的方案,并给出具体的计算方法.
距离的方案,并给出具体的计算方法.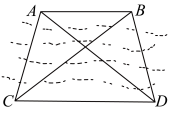
您最近一年使用:0次
名校
解题方法
2 . 某市遇到洪涝灾害.在该市的某湖泊的岸边的O点处(湖岸可视为直线)停放着一艘搜救小船,由于缆绳突然断开,小船被风刮跑(假设小船沿直线匀速漂移).
现有两种方案:
①如图1,在湖岸设置一个观察点A,A点距离O点20m.当小船在漂移到B处时,测得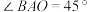 ;经过15s,小船漂移到C处,测得
;经过15s,小船漂移到C处,测得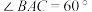 .又在O点处测量得小船的漂移方向与河岸成30°.请根据以上数据,计算小船的漂移速度.
.又在O点处测量得小船的漂移方向与河岸成30°.请根据以上数据,计算小船的漂移速度.
②如图2,在岸边设置两个观察点A,B,且A,B之间的直线距离为20m,当小船在C处时,测得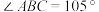 和
和 ;经过20s,小船漂移到D处,测得
;经过20s,小船漂移到D处,测得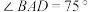 和
和 .请根据以上数据,计算小船的漂移速度.
.请根据以上数据,计算小船的漂移速度.
(2)如图3,若小船从点O开始漂移的同时,在O点处的一名安全员沿河岸以4km/h开始追赶小船,在此过程中获知小船的漂移方向与河岸成30°,漂移的速度为2.2km/h,于是安全员在河岸上选择合适的地点A下水,以2km/h的速度游泳沿直线追赶小船.问安全员是否能追上小船?请说明理由.
参考数据: ,
, ,
, ,
,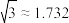 .
.
现有两种方案:
①如图1,在湖岸设置一个观察点A,A点距离O点20m.当小船在漂移到B处时,测得
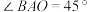 ;经过15s,小船漂移到C处,测得
;经过15s,小船漂移到C处,测得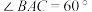 .又在O点处测量得小船的漂移方向与河岸成30°.请根据以上数据,计算小船的漂移速度.
.又在O点处测量得小船的漂移方向与河岸成30°.请根据以上数据,计算小船的漂移速度.②如图2,在岸边设置两个观察点A,B,且A,B之间的直线距离为20m,当小船在C处时,测得
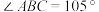 和
和 ;经过20s,小船漂移到D处,测得
;经过20s,小船漂移到D处,测得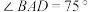 和
和 .请根据以上数据,计算小船的漂移速度.
.请根据以上数据,计算小船的漂移速度.(2)如图3,若小船从点O开始漂移的同时,在O点处的一名安全员沿河岸以4km/h开始追赶小船,在此过程中获知小船的漂移方向与河岸成30°,漂移的速度为2.2km/h,于是安全员在河岸上选择合适的地点A下水,以2km/h的速度游泳沿直线追赶小船.问安全员是否能追上小船?请说明理由.
参考数据:
 ,
, ,
, ,
,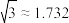 .
.
您最近一年使用:0次
3 . 如图,已知两个路灯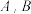 之间的距离是
之间的距离是 ,为了测量点
,为了测量点 与河对岸(不可到达)点
与河对岸(不可到达)点 之间的距离,先后测得
之间的距离,先后测得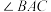 和
和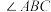 的大小.
的大小. ,求
,求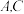 两点之间的距离;
两点之间的距离;
(2)假设你只携带量角器(可以测量以你为顶点的角的大小).请你设计一个可以计算出 河对岸两点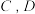 之间距离的方案,包括:
之间距离的方案,包括:
①指出要测量的数据并标示在图中;
②用文字和公式写出计算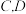 之间距离的步骤.
之间距离的步骤.
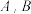 之间的距离是
之间的距离是 ,为了测量点
,为了测量点 与河对岸(不可到达)点
与河对岸(不可到达)点 之间的距离,先后测得
之间的距离,先后测得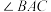 和
和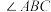 的大小.
的大小.
 ,求
,求 两点之间的距离;
两点之间的距离;(2)假设你只携带量角器(可以测量以你为顶点的角的大小).请你设计一个可以计算出 河对岸两点
 之间距离的方案,包括:
之间距离的方案,包括:①指出要测量的数据并标示在图中;
②用文字和公式写出计算
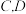 之间距离的步骤.
之间距离的步骤.
您最近一年使用:0次
解题方法
4 . 某街道规划建一座口袋公园.如图所示,公园由扇形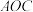 区域和三角形
区域和三角形 区域组成.其中
区域组成.其中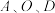 三点共线,扇形半径
三点共线,扇形半径 为30米.规划口袋公园建成后,扇形
为30米.规划口袋公园建成后,扇形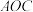 区域将作为花草展示区,三角形
区域将作为花草展示区,三角形 区域作为亲水平台区,两个区域的所有边界修建休闲步道.
区域作为亲水平台区,两个区域的所有边界修建休闲步道. ,
,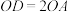 ,求休闲步道总长(精确到米);
,求休闲步道总长(精确到米);
(2)若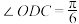 ,在前期民意调查时发现,绝大部分街道居民对亲水平台区更感兴趣.请你根据民意调查情况,从该区域面积最大或周长最长的视角出发,选择其中一个方案,设计三角形
,在前期民意调查时发现,绝大部分街道居民对亲水平台区更感兴趣.请你根据民意调查情况,从该区域面积最大或周长最长的视角出发,选择其中一个方案,设计三角形 的形状.
的形状.
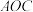 区域和三角形
区域和三角形 区域组成.其中
区域组成.其中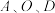 三点共线,扇形半径
三点共线,扇形半径 为30米.规划口袋公园建成后,扇形
为30米.规划口袋公园建成后,扇形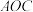 区域将作为花草展示区,三角形
区域将作为花草展示区,三角形 区域作为亲水平台区,两个区域的所有边界修建休闲步道.
区域作为亲水平台区,两个区域的所有边界修建休闲步道.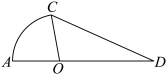
 ,
,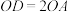 ,求休闲步道总长(精确到米);
,求休闲步道总长(精确到米);(2)若
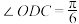 ,在前期民意调查时发现,绝大部分街道居民对亲水平台区更感兴趣.请你根据民意调查情况,从该区域面积最大或周长最长的视角出发,选择其中一个方案,设计三角形
,在前期民意调查时发现,绝大部分街道居民对亲水平台区更感兴趣.请你根据民意调查情况,从该区域面积最大或周长最长的视角出发,选择其中一个方案,设计三角形 的形状.
的形状.
您最近一年使用:0次
5 . 10世纪波斯著名数学家、天文学家阿尔·库希设计出一种方案,通过两个观测者异地同时观察同一颗流星,来测定其发射点的高度,如图,假设地球是一个标准的球体, 为地球的球心,弧
为地球的球心,弧 为地线,有两个观测者在地球上的
为地线,有两个观测者在地球上的 两地同时观测到一颗流星
两地同时观测到一颗流星 ,观测的仰角分别为
,观测的仰角分别为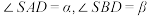 ,其中
,其中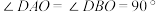 ,为了方便计算,我们考虑一种理想状态,假设两个观测者在地球上的
,为了方便计算,我们考虑一种理想状态,假设两个观测者在地球上的 两点测得
两点测得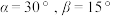 ,地球半径为
,地球半径为 千米,两个观测者的距离弧
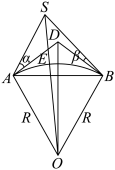
千米,两个观测者的距离弧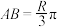 千米.(参考数据:
千米.(参考数据: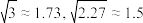 )
) 发射点的近似高度
发射点的近似高度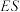 .
.
(2)在古希腊时代,科学不发达,人们看到流星以为这是地球水分蒸发后凝结的固体.已知对流层(地球大气层靠近地面的一层)高度大约在18千米左右,若地球半径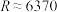 千米,请你据此判断该流星
千米,请你据此判断该流星 是地球蒸发物还是“天外来客”,并说明理由.
是地球蒸发物还是“天外来客”,并说明理由.
 为地球的球心,弧
为地球的球心,弧 为地线,有两个观测者在地球上的
为地线,有两个观测者在地球上的 两地同时观测到一颗流星
两地同时观测到一颗流星 ,观测的仰角分别为
,观测的仰角分别为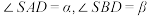 ,其中
,其中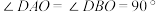 ,为了方便计算,我们考虑一种理想状态,假设两个观测者在地球上的
,为了方便计算,我们考虑一种理想状态,假设两个观测者在地球上的 两点测得
两点测得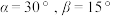 ,地球半径为
,地球半径为 千米,两个观测者的距离弧
千米,两个观测者的距离弧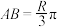 千米.(参考数据:
千米.(参考数据: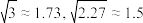 )
)
 发射点的近似高度
发射点的近似高度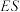 .
.(2)在古希腊时代,科学不发达,人们看到流星以为这是地球水分蒸发后凝结的固体.已知对流层(地球大气层靠近地面的一层)高度大约在18千米左右,若地球半径
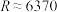 千米,请你据此判断该流星
千米,请你据此判断该流星 是地球蒸发物还是“天外来客”,并说明理由.
是地球蒸发物还是“天外来客”,并说明理由.
您最近一年使用:0次
名校
解题方法
6 . 在 中,
中, 分别为内角
分别为内角 所对的边,且满足
所对的边,且满足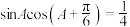 .
.
(1)求角 的大小;
的大小;
(2)试从条件①②③中选出两个作为已知,使得 存在且唯一,并以此为依据求
存在且唯一,并以此为依据求 的面积.(注:只需写出一个选定方案即可)
的面积.(注:只需写出一个选定方案即可)
条件①: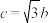 ;条件②:
;条件②: ;条件③:
;条件③: .
.
 中,
中, 分别为内角
分别为内角 所对的边,且满足
所对的边,且满足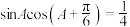 .
.(1)求角
 的大小;
的大小;(2)试从条件①②③中选出两个作为已知,使得
 存在且唯一,并以此为依据求
存在且唯一,并以此为依据求 的面积.(注:只需写出一个选定方案即可)
的面积.(注:只需写出一个选定方案即可)条件①:
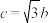 ;条件②:
;条件②: ;条件③:
;条件③: .
.
您最近一年使用:0次
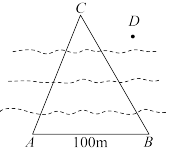
7 . 如图,某人位于临河的公路上,已知公路两个相邻路灯 、
、 之间的距离是
之间的距离是 ,为了测量点
,为了测量点 与河对岸一点
与河对岸一点 之间的距离,此人先后测得
之间的距离,此人先后测得 ,
, .
. 、
、 两点之间的距离;
两点之间的距离;
(2)假设你只携带着量角器(可以测量以你为顶点的角的大小).请你设计一个通过测量角可以计算出河对岸两点 、
、 之间距离的方案,用字母表示所测量的角的大小,并用其表示出
之间距离的方案,用字母表示所测量的角的大小,并用其表示出 的长.
的长.
 、
、 之间的距离是
之间的距离是 ,为了测量点
,为了测量点 与河对岸一点
与河对岸一点 之间的距离,此人先后测得
之间的距离,此人先后测得 ,
, .
.
 、
、 两点之间的距离;
两点之间的距离;(2)假设你只携带着量角器(可以测量以你为顶点的角的大小).请你设计一个通过测量角可以计算出河对岸两点
 、
、 之间距离的方案,用字母表示所测量的角的大小,并用其表示出
之间距离的方案,用字母表示所测量的角的大小,并用其表示出 的长.
的长.
您最近一年使用:0次
名校
解题方法
8 . 在 中,a,b,c分别为内角A,B,C所对的边,且满足
中,a,b,c分别为内角A,B,C所对的边,且满足 .
.
(1)求角A的大小;
(2)试从条件①②③中选出两个作为已知,使得 存在且唯一,写出你的选择___________,并以此为依据求
存在且唯一,写出你的选择___________,并以此为依据求 的面积.(注:只需写出一个选定方案即可)
的面积.(注:只需写出一个选定方案即可)
条件①: ;条件②:
;条件②: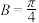 ;条件③:
;条件③: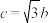 .
.
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
 中,a,b,c分别为内角A,B,C所对的边,且满足
中,a,b,c分别为内角A,B,C所对的边,且满足 .
.(1)求角A的大小;
(2)试从条件①②③中选出两个作为已知,使得
 存在且唯一,写出你的选择___________,并以此为依据求
存在且唯一,写出你的选择___________,并以此为依据求 的面积.(注:只需写出一个选定方案即可)
的面积.(注:只需写出一个选定方案即可)条件①:
 ;条件②:
;条件②: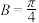 ;条件③:
;条件③: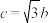 .
.注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
您最近一年使用:0次
2023-05-26更新
|
1186次组卷
|
6卷引用:专题01 条件开放型【练】【北京版】



