名校
解题方法
1 . 已知函数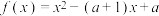 .
.
(1)当 时,求关于
时,求关于 的不等式
的不等式 的解集;
的解集;
(2)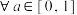 ,关于
,关于 的方程
的方程 在
在 总有两个不同实数解,求实数
总有两个不同实数解,求实数 的取值范围;
的取值范围;
(3)若 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
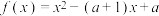 .
.(1)当
 时,求关于
时,求关于 的不等式
的不等式 的解集;
的解集;(2)
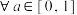 ,关于
,关于 的方程
的方程 在
在 总有两个不同实数解,求实数
总有两个不同实数解,求实数 的取值范围;
的取值范围;(3)若
 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-01-01更新
|
408次组卷
|
2卷引用:重庆市渝北区松树桥中学校2023-2024学年高一上学期第三次诊断数学试题
名校
解题方法
2 . 已知定义在 上的偶函数
上的偶函数 和奇函数
和奇函数 满足
满足 ,
,
(1)求 的最小值.
的最小值.
(2)若对任意的 ,
, 恒成立,则实数
恒成立,则实数 的取值范围.
的取值范围.
 上的偶函数
上的偶函数 和奇函数
和奇函数 满足
满足 ,
,(1)求
 的最小值.
的最小值.(2)若对任意的
 ,
, 恒成立,则实数
恒成立,则实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
3 . 已知 为偶函数、
为偶函数、 为奇函数,且满足
为奇函数,且满足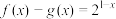 .
.
(1)求 ,
, ;
;
(2)若方程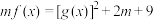 有解,求实数m的取值范围.
有解,求实数m的取值范围.
 为偶函数、
为偶函数、 为奇函数,且满足
为奇函数,且满足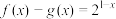 .
.(1)求
 ,
, ;
;(2)若方程
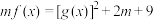 有解,求实数m的取值范围.
有解,求实数m的取值范围.
您最近一年使用:0次
2023-12-20更新
|
936次组卷
|
3卷引用:重庆市忠县中学2023-2024学年高一上学期12月云班检测数学试题
重庆市忠县中学2023-2024学年高一上学期12月云班检测数学试题福建省福州第四中学2023-2024学年高一上学期模块检测数学试卷(已下线)第四章 指数函数与对数函数(章末测试B卷)-同步精品课堂(人教A版2019必修第一册)
名校
4 . 为了保护水资源,提倡节约用水,某城市对居民生活用水实行“阶梯水价”,计费方法如下表:
(1)求用户每月缴纳水费 (单位:元)与每月用水量
(单位:元)与每月用水量 (单位:
(单位: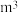 )的函数关系式;
)的函数关系式;
(2)随着生活水平的提高,人们对生活的品质有了更高的要求,经验表明,当居民用水量在一定范围内时,若随性用水,用水量增加,生活越方便;若时刻想着节约用水,生活也会麻烦.数据表明,人们的“幸福感指数” 与缴纳水费
与缴纳水费 及“生活麻烦系数”
及“生活麻烦系数” 存在以下关系:
存在以下关系: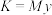 (其中
(其中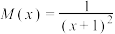 ),当某居民用水量超过
),当某居民用水量超过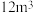 时,求该居民“幸福感指数”
时,求该居民“幸福感指数” 的最大值及此时的用水量
的最大值及此时的用水量
| 每户每月用水量 | 水价 |
不超过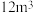 的部分 的部分 | 3元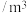 |
超过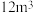 但不超过 但不超过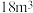 的部分 的部分 | 6元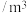 |
超过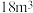 的部分 的部分 | 8元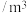 |
 (单位:元)与每月用水量
(单位:元)与每月用水量 (单位:
(单位: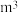 )的函数关系式;
)的函数关系式;(2)随着生活水平的提高,人们对生活的品质有了更高的要求,经验表明,当居民用水量在一定范围内时,若随性用水,用水量增加,生活越方便;若时刻想着节约用水,生活也会麻烦.数据表明,人们的“幸福感指数”
 与缴纳水费
与缴纳水费 及“生活麻烦系数”
及“生活麻烦系数” 存在以下关系:
存在以下关系: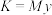 (其中
(其中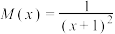 ),当某居民用水量超过
),当某居民用水量超过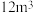 时,求该居民“幸福感指数”
时,求该居民“幸福感指数” 的最大值及此时的用水量
的最大值及此时的用水量
您最近一年使用:0次
名校
解题方法
5 . (1)已知 ,求
,求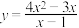 的最小值;
的最小值;
(2)若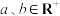 ,且满足条件
,且满足条件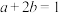 ,求
,求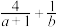 的最小值.
的最小值.
 ,求
,求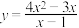 的最小值;
的最小值;(2)若
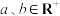 ,且满足条件
,且满足条件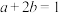 ,求
,求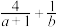 的最小值.
的最小值.
您最近一年使用:0次
名校
解题方法
6 . 某企业为了增加工作岗位和增加员工收入,投入90万元安装了一套新的生产设备,预计使用该设备后前 年的总支出成本为
年的总支出成本为 万元,每年的销售收入95万元.设使用该设备前
万元,每年的销售收入95万元.设使用该设备前 年的总盈利额为
年的总盈利额为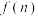 万元.
万元.
(1)写出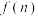 关于
关于 的函数关系式,并估计该设备从第几年开始盈利;
的函数关系式,并估计该设备从第几年开始盈利;
(2)使用若干年后对该设备处理的方案有两种:
方案一:当总盈利额达到最大值时,该设备以20万元的价格处理;
方案二:当年平均盈利额达到最大值时,该设备以70万元的价格处理;
问哪种方案较为合理?并说明理由.
 年的总支出成本为
年的总支出成本为 万元,每年的销售收入95万元.设使用该设备前
万元,每年的销售收入95万元.设使用该设备前 年的总盈利额为
年的总盈利额为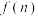 万元.
万元.(1)写出
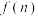 关于
关于 的函数关系式,并估计该设备从第几年开始盈利;
的函数关系式,并估计该设备从第几年开始盈利;(2)使用若干年后对该设备处理的方案有两种:
方案一:当总盈利额达到最大值时,该设备以20万元的价格处理;
方案二:当年平均盈利额达到最大值时,该设备以70万元的价格处理;
问哪种方案较为合理?并说明理由.
您最近一年使用:0次
解题方法
7 . 记 的内角A,B,C的对边分别为a,b,c,满足
的内角A,B,C的对边分别为a,b,c,满足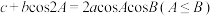 .
.
(1)求 ;
;
(2)若角 的平分线交
的平分线交 于
于 点,且
点,且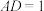 ,求
,求 面积的最小值.
面积的最小值.
 的内角A,B,C的对边分别为a,b,c,满足
的内角A,B,C的对边分别为a,b,c,满足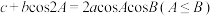 .
.(1)求
 ;
;(2)若角
 的平分线交
的平分线交 于
于 点,且
点,且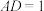 ,求
,求 面积的最小值.
面积的最小值.
您最近一年使用:0次
2023-12-16更新
|
879次组卷
|
4卷引用:重庆市部分学校2024届高三上学期第四次联考数学试题
重庆市部分学校2024届高三上学期第四次联考数学试题安徽省“皖江名校联盟”2024届高三上学期12月月考数学试题(已下线)重难点01 利用基本不等式求最值【八大题型】(已下线)微专题02 解三角形最值、范围与图形题型归类
名校
解题方法
8 . 已知 是实数,且满足
是实数,且满足 ,证明下列命题:
,证明下列命题:
(1)“ ”是“
”是“ ”的充要条件;
”的充要条件;
(2)“ ”是“
”是“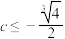 ”的充分条件.
”的充分条件.
 是实数,且满足
是实数,且满足 ,证明下列命题:
,证明下列命题:(1)“
 ”是“
”是“ ”的充要条件;
”的充要条件;(2)“
 ”是“
”是“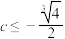 ”的充分条件.
”的充分条件.
您最近一年使用:0次
2023-12-15更新
|
109次组卷
|
2卷引用:重庆市部分学校2023-2024学年高一上学期期中数学试题
解题方法
9 . 已知函数 .
.
(1)解不等式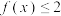 ;
;
(2)记函数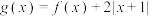 的最小值为
的最小值为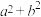 ,求证:
,求证: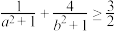 .
.
 .
.(1)解不等式
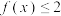 ;
;(2)记函数
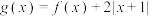 的最小值为
的最小值为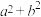 ,求证:
,求证: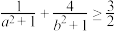 .
.
您最近一年使用:0次
名校
解题方法
10 . 国内某大型机械加工企业在过去的一个月内(共计30天,包括第30天),其主营产品在第x天的指导价为每件 (元),且满足
(元),且满足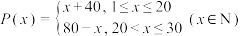 ,第
,第 天的日交易量
天的日交易量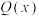 (万件)的部分数据如下表:
(万件)的部分数据如下表:
(1)给出以下两种函数模型:①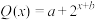 ,②
,② ,其中
,其中 为常数. 请你根据上表中的数据,从①②中选择你认为最合适的一种函数模型来拟合该产品日交易量
为常数. 请你根据上表中的数据,从①②中选择你认为最合适的一种函数模型来拟合该产品日交易量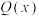 (万件)的函数关系;并且从四组数据中选择你认为最简洁合理的两组数据进行合理的推理和运算,求出
(万件)的函数关系;并且从四组数据中选择你认为最简洁合理的两组数据进行合理的推理和运算,求出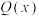 的函数关系式;
的函数关系式;
(2)若该企业在未来一个月(共计 天,包括第
天,包括第 天)的生产经营水平维持上个月的水平基本不变,由(1)预测并求出该企业在未来一个月内第
天)的生产经营水平维持上个月的水平基本不变,由(1)预测并求出该企业在未来一个月内第 天的日交易额
天的日交易额 的函数关系式,并确定
的函数关系式,并确定 取得最小值时对应的
取得最小值时对应的 .
.
 (元),且满足
(元),且满足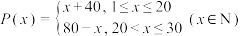 ,第
,第 天的日交易量
天的日交易量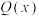 (万件)的部分数据如下表:
(万件)的部分数据如下表:第x天 | 1 | 2 | 5 | 10 |
Q(x)(万件) | 14.01 | 12 | 10.8 | 10.38 |
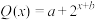 ,②
,② ,其中
,其中 为常数. 请你根据上表中的数据,从①②中选择你认为最合适的一种函数模型来拟合该产品日交易量
为常数. 请你根据上表中的数据,从①②中选择你认为最合适的一种函数模型来拟合该产品日交易量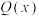 (万件)的函数关系;并且从四组数据中选择你认为最简洁合理的两组数据进行合理的推理和运算,求出
(万件)的函数关系;并且从四组数据中选择你认为最简洁合理的两组数据进行合理的推理和运算,求出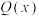 的函数关系式;
的函数关系式;(2)若该企业在未来一个月(共计
 天,包括第
天,包括第 天)的生产经营水平维持上个月的水平基本不变,由(1)预测并求出该企业在未来一个月内第
天)的生产经营水平维持上个月的水平基本不变,由(1)预测并求出该企业在未来一个月内第 天的日交易额
天的日交易额 的函数关系式,并确定
的函数关系式,并确定 取得最小值时对应的
取得最小值时对应的 .
.
您最近一年使用:0次
2023-12-15更新
|
416次组卷
|
5卷引用:重庆市名校联盟2023-2024学年高一上学期第二次联考(12月)数学试题
重庆市名校联盟2023-2024学年高一上学期第二次联考(12月)数学试题(已下线)高一上学期第三次月考数学模拟试卷(第1章-第4章)-【题型分类归纳】(人教A版2019必修第一册)(已下线)【第三课】4.5.3函数模型的应用 上好三课,做好三套题,高中数学素养晋级之路江西省新余市2023-2024学年高一上学期期末质量检测数学试卷江苏省东台市2023-2024学年高一上学期期末考试数学试题



