名校
解题方法
1 . 设直线l的方程为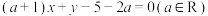 .
.
(1)求证:不论a为何值,直线l必过一定点P;
(2)若直线l分别与x轴正半轴,y轴正半轴交于点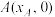 ,
,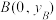 ,当
,当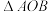 面积最小时,求此时的直线方程;
面积最小时,求此时的直线方程;
(3)当直线l在两坐标轴上的截距均为正整数且a也为正整数时,求直线l的方程.
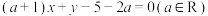 .
.(1)求证:不论a为何值,直线l必过一定点P;
(2)若直线l分别与x轴正半轴,y轴正半轴交于点
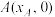 ,
,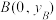 ,当
,当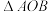 面积最小时,求此时的直线方程;
面积最小时,求此时的直线方程;(3)当直线l在两坐标轴上的截距均为正整数且a也为正整数时,求直线l的方程.
您最近一年使用:0次
2024-07-07更新
|
1106次组卷
|
6卷引用:福建省泉州市晋江市侨声中学2024-2025学年高二上学期教学质量监测(一)数学试卷
名校
解题方法
2 . 已知直线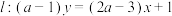 .
.
(1)求证:直线 过定点;
过定点;
(2)若直线 不经过第二象限,求实数
不经过第二象限,求实数 的取值范围;
的取值范围;
(3)若直线 与两坐标轴的正半轴围成的三角形面积最小,求
与两坐标轴的正半轴围成的三角形面积最小,求 的方程.
的方程.
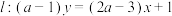 .
.(1)求证:直线
 过定点;
过定点;(2)若直线
 不经过第二象限,求实数
不经过第二象限,求实数 的取值范围;
的取值范围;(3)若直线
 与两坐标轴的正半轴围成的三角形面积最小,求
与两坐标轴的正半轴围成的三角形面积最小,求 的方程.
的方程.
您最近一年使用:0次
2024-06-28更新
|
3172次组卷
|
9卷引用:福建省厦门市松柏中学2024-2025学年高二上学期月考1数学试卷
福建省厦门市松柏中学2024-2025学年高二上学期月考1数学试卷浙江省宁波市九校2023-2024学年高一下学期期末联考数学试题(已下线)第07讲 直线的方程-【暑假自学课】(人教B版2019选择性必修第一册)河北省邯郸市涉县第一中学2024-2025学年高二上学期7月月考数学试题江苏省如东高级中学2024-2025学年高二上学期开学第一次考试数学试题 吉林省白城市第一中学2024-2025学年高二上学期10月期中考试数学试题浙江省金华市义乌市第二中学2024-2025学年高二上学期10月统测数学试题广东省五校2024-2025学年高二10月联考(一)数学试卷甘肃省兰州第一中学2024-2025学年高二上学期10月月考数学试题
解题方法
3 . 已知直线 :
: .
.
(1)证明无论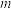 为何值,直线
为何值,直线 与直线
与直线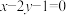 总相交;
总相交;
(2)若 为坐标原点,直线
为坐标原点,直线 与
与 ,
,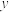 轴的正半轴分别交于
轴的正半轴分别交于 两点,求
两点,求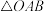 面积的最小值.
面积的最小值.
 :
: .
.(1)证明无论
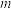 为何值,直线
为何值,直线 与直线
与直线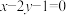 总相交;
总相交;(2)若
 为坐标原点,直线
为坐标原点,直线 与
与 ,
,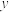 轴的正半轴分别交于
轴的正半轴分别交于 两点,求
两点,求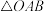 面积的最小值.
面积的最小值.
您最近一年使用:0次
2022-10-15更新
|
643次组卷
|
6卷引用:福建省建瓯市芝华中学2023-2024学年高二上学期第一次阶段考试数学试题
福建省建瓯市芝华中学2023-2024学年高二上学期第一次阶段考试数学试题山东省2022-2023学年高二10月联合调考数学试题C广东省部分学校2022-2023学年高二上学期质量检测联合调考(10月)数学试题(已下线)期中押题预测卷(考试范围:选择性必修第一册)(拔高卷)-【单元测试】2022-2023学年高二数学分层训练AB卷(人教B版2019)河北省邯郸市鸡泽县第一中学2023-2024学年高二上学期第一次月考数学试题(已下线)高二数学上学期第一次月考模拟卷(空间向量与立体几何+直线的方程)-【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)
名校
解题方法
4 . 已知一条动直线 ,
,
(1)求证:直线恒过定点,并求出定点P的坐标;
(2)若直线不经过第二象限,求m的取值范围;
(3)若直线与x、y轴的正半轴分别交于A,B两点,O为坐标原点, 的面积为6,求直线的方程.
的面积为6,求直线的方程.
 ,
,(1)求证:直线恒过定点,并求出定点P的坐标;
(2)若直线不经过第二象限,求m的取值范围;
(3)若直线与x、y轴的正半轴分别交于A,B两点,O为坐标原点,
 的面积为6,求直线的方程.
的面积为6,求直线的方程.
您最近一年使用:0次
2022-01-02更新
|
1234次组卷
|
8卷引用:福建省厦门市厦门大学附属科技中学2023-2024学年高二上学期第一次阶段性测试数学试题
福建省厦门市厦门大学附属科技中学2023-2024学年高二上学期第一次阶段性测试数学试题云南省楚雄市天人中学2021-2022学年高二(A层)10月学习效果监测数学试题(已下线)1.2 直线的方程(1)(已下线)突破2.2 直线的方程(2)(课时训练)(已下线)专题2.6 直线的方程(二)-重难点题型检测-2022-2023学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)第14讲 直线的方程8种常见考法归类(2)(已下线)专题2.12 直线和圆的方程全章综合测试卷(提高篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)(已下线)2.2.3 直线的一般式方程——课后作业(提升版)
名校
解题方法
5 . 已知直线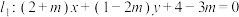 .
.
(1)求证:无论 为何实数,直线
为何实数,直线 恒过一定点
恒过一定点 ;
;
(2)若直线 过点
过点 ,且与
,且与 轴负半轴、
轴负半轴、 轴负半轴围成三角形面积最小,求直线
轴负半轴围成三角形面积最小,求直线 的方程.
的方程.
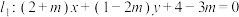 .
.(1)求证:无论
 为何实数,直线
为何实数,直线 恒过一定点
恒过一定点 ;
;(2)若直线
 过点
过点 ,且与
,且与 轴负半轴、
轴负半轴、 轴负半轴围成三角形面积最小,求直线
轴负半轴围成三角形面积最小,求直线 的方程.
的方程.
您最近一年使用:0次
2021-08-20更新
|
2644次组卷
|
19卷引用:福建省泉州市永春第一中学2021-2022学年高二9月线上考试数学试题
福建省泉州市永春第一中学2021-2022学年高二9月线上考试数学试题重庆市铜梁县第一中学2017-2018学年高二10月月考数学(理)试题【全国百强校】四川省雅安中学2018-2019学年高二上学期期中考试数学(文)试题人教A版(2019) 选择性必修第一册 过关斩将 第二章 直线和圆的方程 2.3.1 两条直线的交点坐标 2.3.2 两点间的距离公式江西省宜春市天立高级中学2020-2021学年高一下学期期末数学试题(已下线)课时2.3.1 直线的交点坐标与距离公式(01)-2021-2022学年高二数学同步练习和分类专题教案(人教A版2019选择性必修第一册)江苏省苏州市星海实验中学2021-2022学年高二上学期10月学情调研数学试题(已下线)卷02 直线与圆的方程-章节重难点突破卷 -【重难点突破】2021-2022学年高二数学上册常考题专练(人教A版2019选择性必修第一册)(已下线)2.2.3 直线的一般式方程(同步练习)-【一堂好课】2021-2022学年高二数学上学期同步精品课堂(人教A版2019选择性必修第一册) 安徽省安庆市桐城市第八中学2021-2022学年高二上学期第一次月考数学试题河南省鹤壁市浚县浚县第一中学2021-2022学年高一下学期7月月考数学试题直线的交点坐标与距离公式江苏省江浦高级中学(文昌校区)、秦淮中学、玄武高级中学2022-2023学年高二上学期10月学情调研数学试题江苏省南京市2022-2023学年高二上学期10月学情调研数学试题浙江省嘉兴市桐乡市高级中学2022-2023学年高二上学期9月检测数学试题2.3.1 两条直线的交点坐标练习河北省保定市定州市第二中学2023-2024学年高二上学期10月月考数学试题山西省太原市第五中学校2023-2024学年高二上学期10月月考数学试题河北省秦皇岛市青龙满族自治县实验中学2023-2024学年高二上学期10月月考数学试题
名校
解题方法
6 . 直线 过点
过点 且与
且与 轴、
轴、 轴正半轴分别交于
轴正半轴分别交于 、
、 两点.
两点.
(1)若直线 的斜率为
的斜率为 ,求△
,求△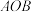 的面积;
的面积;
(2)若△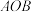 的面积
的面积 满足
满足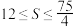 ,求直线
,求直线 的斜率
的斜率 的取值范围;
的取值范围;
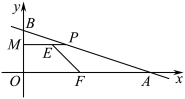
(3)如图,若点 分向量
分向量 所成的比的值为2,过点
所成的比的值为2,过点 作平行于
作平行于 轴的直线交
轴的直线交 轴于点
轴于点 ,动点
,动点 、
、 分别在线段
分别在线段 和
和 上,若直线
上,若直线 平分直角梯形
平分直角梯形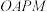 的面积,求证:直线
的面积,求证:直线 必过一定点,并求出该定点坐标.
必过一定点,并求出该定点坐标.
 过点
过点 且与
且与 轴、
轴、 轴正半轴分别交于
轴正半轴分别交于 、
、 两点.
两点.
(1)若直线
 的斜率为
的斜率为 ,求△
,求△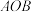 的面积;
的面积;(2)若△
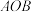 的面积
的面积 满足
满足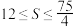 ,求直线
,求直线 的斜率
的斜率 的取值范围;
的取值范围;(3)如图,若点
 分向量
分向量 所成的比的值为2,过点
所成的比的值为2,过点 作平行于
作平行于 轴的直线交
轴的直线交 轴于点
轴于点 ,动点
,动点 、
、 分别在线段
分别在线段 和
和 上,若直线
上,若直线 平分直角梯形
平分直角梯形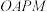 的面积,求证:直线
的面积,求证:直线 必过一定点,并求出该定点坐标.
必过一定点,并求出该定点坐标.
您最近一年使用:0次
2020-11-12更新
|
297次组卷
|
2卷引用:福建省泉州实验中学2021-2022学年高二10月月考数学试题
名校
解题方法
7 . 已知直线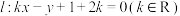
(1)证明直线l过定点并求此点的坐标;
(2)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设 的面积为S,求S的最小值及此时直线l的方程.
的面积为S,求S的最小值及此时直线l的方程.
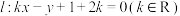
(1)证明直线l过定点并求此点的坐标;
(2)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设
 的面积为S,求S的最小值及此时直线l的方程.
的面积为S,求S的最小值及此时直线l的方程.
您最近一年使用:0次
2020-11-22更新
|
324次组卷
|
2卷引用:福建省莆田第三中学,励志学校2023-2024学年高二上学期期中联考数学试卷



