1 . 已知椭圆 过
过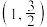 和
和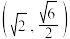 两点.
两点.
(1)求椭圆C的方程;
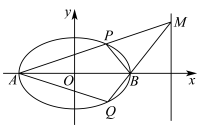
(2)如图所示,记椭圆的左、右顶点分别为A,B,当动点M在定直线 上运动时,直线
上运动时,直线 ,
, 分别交椭圆于两点P和Q.
分别交椭圆于两点P和Q.
(i)证明:点B在以 为直径的圆内;
为直径的圆内;
(ii)求四边形 面积的最大值.
面积的最大值.
 过
过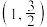 和
和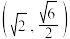 两点.
两点.
(1)求椭圆C的方程;
(2)如图所示,记椭圆的左、右顶点分别为A,B,当动点M在定直线
 上运动时,直线
上运动时,直线 ,
, 分别交椭圆于两点P和Q.
分别交椭圆于两点P和Q.(i)证明:点B在以
 为直径的圆内;
为直径的圆内;(ii)求四边形
 面积的最大值.
面积的最大值.
您最近一年使用:0次
2023-09-19更新
|
1983次组卷
|
9卷引用:四川省资阳市乐至中学2023-2024学年高二上学期期中数学试题
四川省资阳市乐至中学2023-2024学年高二上学期期中数学试题湖南省长沙市第一中学2024届高三上学期月考(二)数学试题(已下线)高二上学期期中复习【第三章 圆锥曲线的方程】十二大题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第一册)广东省佛山市南海区九江中学2024届高三上学期10月月考数学试题(已下线)重难点突破07 圆锥曲线三角形面积与四边形面积题型全归类(七大题型)(已下线)重难点突破15 圆锥曲线中的圆问题(四大题型)湖南省衡阳市衡阳县第二中学2023-2024学年高二上学期期中数学试题江西省宜春市丰城市第九中学2024届高三上学期12月月考数学试题(已下线)第3章 圆锥曲线与方程章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第一册)
2 . 已知圆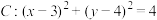 .
.
(1)若直线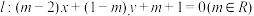 ,证明:无论
,证明:无论 为何值,直线
为何值,直线 都与圆
都与圆 相交;
相交;
(2)若过点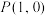 的直线
的直线 与圆
与圆 相交于
相交于 两点,求
两点,求 的面积的最大值,并求此时直线
的面积的最大值,并求此时直线 的方程.
的方程.
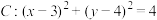 .
.(1)若直线
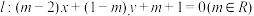 ,证明:无论
,证明:无论 为何值,直线
为何值,直线 都与圆
都与圆 相交;
相交;(2)若过点
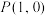 的直线
的直线 与圆
与圆 相交于
相交于 两点,求
两点,求 的面积的最大值,并求此时直线
的面积的最大值,并求此时直线 的方程.
的方程.
您最近一年使用:0次
2022-04-08更新
|
1536次组卷
|
7卷引用:四川省眉山市眉山北外附属东坡外国语学校2022-2023学年高二上学期9月月考数学试题
四川省眉山市眉山北外附属东坡外国语学校2022-2023学年高二上学期9月月考数学试题四川省成都市双流区双流中学2023-2024学年高二上学期10月月考数学试题重庆市两江中学校(教育集团)2021-2022学年高二上学期第一次月考数学试题(已下线)第14讲 直线与圆、圆与圆的位置关系-【暑假自学课】2022年新高二数学暑假精品课(人教版2019必修第二册+选择性必修第一册)广东省普宁市华侨中学2022-2023学年高二上学期期中数学试题黑龙江省鸡西市虎林市高级中学2022-2023学年高二上学期9月月考数学试题湖南省雅礼集团2024-2025学年高二下学期第一次月考数学试卷
名校
解题方法
3 . 如图,在平面直角坐标系 中,已知抛物线C:
中,已知抛物线C: 的焦点为F,准线为l,过点F且斜率大于0的直线交抛物线C于A,B两点,过线段AB的中点M且与x轴平行的直线依次交直线OA,OB,l于点P,Q,N.
的焦点为F,准线为l,过点F且斜率大于0的直线交抛物线C于A,B两点,过线段AB的中点M且与x轴平行的直线依次交直线OA,OB,l于点P,Q,N.
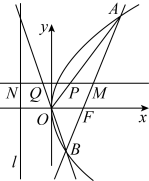
(1)判断线段PM与NQ长度的大小关系,并证明你的结论;
(2)若线段NP上的任意一点均在以点Q为圆心、线段QO长为半径的圆内或圆上,求直线AB斜率的取值范围.
 中,已知抛物线C:
中,已知抛物线C: 的焦点为F,准线为l,过点F且斜率大于0的直线交抛物线C于A,B两点,过线段AB的中点M且与x轴平行的直线依次交直线OA,OB,l于点P,Q,N.
的焦点为F,准线为l,过点F且斜率大于0的直线交抛物线C于A,B两点,过线段AB的中点M且与x轴平行的直线依次交直线OA,OB,l于点P,Q,N.
(1)判断线段PM与NQ长度的大小关系,并证明你的结论;
(2)若线段NP上的任意一点均在以点Q为圆心、线段QO长为半径的圆内或圆上,求直线AB斜率的取值范围.
您最近一年使用:0次
2022-05-05更新
|
1044次组卷
|
4卷引用:四川省宜宾市叙州区第一中学校2023届高三三诊模拟考试数学(理)试题
四川省宜宾市叙州区第一中学校2023届高三三诊模拟考试数学(理)试题四川省宜宾市叙州区第一中学校2023届高三三诊模拟数学(文)试题江苏省苏锡常镇四市2022届高三下学期5月教学情况调研(二)数学试题(已下线)考点23圆锥曲线综合应用-2-(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)



