解题方法
1 . 已知椭圆 的焦点在
的焦点在 轴上,经过点
轴上,经过点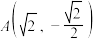 ,
,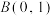 .
.
(1)求 的标准方程;
的标准方程;
(2)定义:若椭圆 上的两个点
上的两个点 ,
,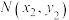 满足
满足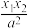
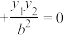 ,则称M,N为该椭圆的一个“共轭点对”,记作
,则称M,N为该椭圆的一个“共轭点对”,记作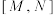 .
.
(i)证明:存在两个点 使得
使得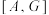 是
是 的“共轭点对”,并求
的“共轭点对”,并求 的坐标;
的坐标;
(ii)设(i)中的两个点 分别为
分别为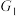 ,
, ,已知过点
,已知过点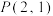 的直线
的直线 与椭圆
与椭圆 交于C,D两点,则直线
交于C,D两点,则直线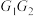 上是否存在定点
上是否存在定点 ,使得直线
,使得直线 与
与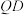 的斜率之积为定值.若存在,求出
的斜率之积为定值.若存在,求出 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 的焦点在
的焦点在 轴上,经过点
轴上,经过点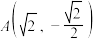 ,
,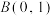 .
.(1)求
 的标准方程;
的标准方程;(2)定义:若椭圆
 上的两个点
上的两个点 ,
,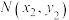 满足
满足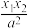
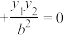 ,则称M,N为该椭圆的一个“共轭点对”,记作
,则称M,N为该椭圆的一个“共轭点对”,记作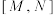 .
.(i)证明:存在两个点
 使得
使得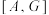 是
是 的“共轭点对”,并求
的“共轭点对”,并求 的坐标;
的坐标;(ii)设(i)中的两个点
 分别为
分别为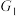 ,
, ,已知过点
,已知过点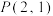 的直线
的直线 与椭圆
与椭圆 交于C,D两点,则直线
交于C,D两点,则直线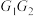 上是否存在定点
上是否存在定点 ,使得直线
,使得直线 与
与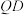 的斜率之积为定值.若存在,求出
的斜率之积为定值.若存在,求出 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
您最近一年使用:0次
解题方法
2 . 已知点T分别与两点 ,
,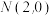 连线的斜率的乘积为
连线的斜率的乘积为 ,
,
(1)求点T的轨迹 的方程;
的方程;
(2)已知直线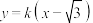 与
与 交于A,B两点,
交于A,B两点, ,求k的值.
,求k的值.
 ,
,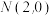 连线的斜率的乘积为
连线的斜率的乘积为 ,
,(1)求点T的轨迹
 的方程;
的方程;(2)已知直线
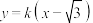 与
与 交于A,B两点,
交于A,B两点, ,求k的值.
,求k的值.
您最近一年使用:0次
名校
解题方法
3 . 已知圆锥曲线C的对称中心在原点,以坐标轴为对称轴,且经过点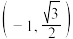 与点
与点 .
.
(1)求曲线C的方程;
(2)已知T为直线 上的动点(T不在x轴上),A,B为曲线C与x轴的交点,直线
上的动点(T不在x轴上),A,B为曲线C与x轴的交点,直线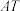 与曲线C相交的另一点为M,直线
与曲线C相交的另一点为M,直线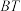 与曲线C相交的另一点为N,记
与曲线C相交的另一点为N,记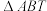 和
和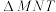 的面积分别为
的面积分别为 ,若
,若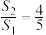 ,求直线
,求直线 的方程.
的方程.
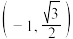 与点
与点 .
.(1)求曲线C的方程;
(2)已知T为直线
 上的动点(T不在x轴上),A,B为曲线C与x轴的交点,直线
上的动点(T不在x轴上),A,B为曲线C与x轴的交点,直线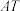 与曲线C相交的另一点为M,直线
与曲线C相交的另一点为M,直线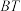 与曲线C相交的另一点为N,记
与曲线C相交的另一点为N,记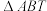 和
和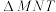 的面积分别为
的面积分别为 ,若
,若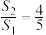 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2024/02/23
|
716次组卷
|
2卷引用:福建省福州第三中学2023-2024学年高二上学期1月期末数学试题
解题方法
4 . 点 在单位圆
在单位圆 上运动,点
上运动,点 的横坐标为点
的横坐标为点 的横坐标的
的横坐标的 倍,纵坐标相同.
倍,纵坐标相同.
(1)求点 的轨迹
的轨迹 的方程;
的方程;
(2)已知 、
、 为曲线
为曲线 与
与 轴的左、右交点,动直线
轴的左、右交点,动直线 交曲线
交曲线 于
于 、
、 两点(均不与
两点(均不与 、
、 重合),记直线
重合),记直线 的斜率为
的斜率为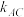 ,直线
,直线 的斜率为
的斜率为 ,且
,且 ,试问动直线
,试问动直线 是否恒过定点?若过,求出该点坐标:若不过,请说明理由.
是否恒过定点?若过,求出该点坐标:若不过,请说明理由.
 在单位圆
在单位圆 上运动,点
上运动,点 的横坐标为点
的横坐标为点 的横坐标的
的横坐标的 倍,纵坐标相同.
倍,纵坐标相同.(1)求点
 的轨迹
的轨迹 的方程;
的方程;(2)已知
 、
、 为曲线
为曲线 与
与 轴的左、右交点,动直线
轴的左、右交点,动直线 交曲线
交曲线 于
于 、
、 两点(均不与
两点(均不与 、
、 重合),记直线
重合),记直线 的斜率为
的斜率为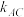 ,直线
,直线 的斜率为
的斜率为 ,且
,且 ,试问动直线
,试问动直线 是否恒过定点?若过,求出该点坐标:若不过,请说明理由.
是否恒过定点?若过,求出该点坐标:若不过,请说明理由.
您最近一年使用:0次
名校
5 . 已知方程 ,其中
,其中 .现有四位同学对该方程进行了判断,提出了四个命题:
.现有四位同学对该方程进行了判断,提出了四个命题:
甲:可以是圆的方程; 乙:可以是抛物线的方程;
丙:可以是椭圆的标准方程; 丁:可以是双曲线的标准方程.
其中,真命题有( )
 ,其中
,其中 .现有四位同学对该方程进行了判断,提出了四个命题:
.现有四位同学对该方程进行了判断,提出了四个命题:甲:可以是圆的方程; 乙:可以是抛物线的方程;
丙:可以是椭圆的标准方程; 丁:可以是双曲线的标准方程.
其中,真命题有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
您最近一年使用:0次
2023/04/19
|
3119次组卷
|
11卷引用:福建省泉州市2023-2024学年高二上学期期末适应性练习数学试题
福建省泉州市2023-2024学年高二上学期期末适应性练习数学试题山东省青岛市第五十八中学2024届高三上学期期末数学试题广东省佛山市2023届高三二模数学试题(已下线)专题01 集合与常用逻辑用语(已下线)专题06 解析几何专题01集合与常用逻辑用语专题17平面解析几何(单选题)(已下线)第05讲 椭圆及其性质(八大题型)(讲义)-1广东省广州市执信中学2024届高三下学期教学情况检测(二)数学试题(已下线)第06讲 双曲线及其性质(十一大题型)(讲义)-1(已下线)易混易错2 分类讨论不全面或分类标准不当(小题狂练)--题型破局系列
名校
6 . 已知点 ,
,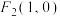 ,
, 为圆
为圆 上的动点,延长
上的动点,延长 至
至 ,使得
,使得 ,
,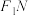 的垂直平分线与
的垂直平分线与 交于点
交于点 ,记
,记 的轨迹为
的轨迹为 .
.
(1)求 的方程;
的方程;
(2)过 的直线
的直线 与
与 交于
交于 两点,纵坐标不为
两点,纵坐标不为 的点
的点 在直线
在直线 上,线段
上,线段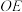 分别与线段
分别与线段 ,
, 交于
交于 两点,且
两点,且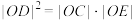 ,证明:
,证明: .
.
 ,
,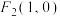 ,
, 为圆
为圆 上的动点,延长
上的动点,延长 至
至 ,使得
,使得 ,
,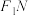 的垂直平分线与
的垂直平分线与 交于点
交于点 ,记
,记 的轨迹为
的轨迹为 .
.(1)求
 的方程;
的方程;(2)过
 的直线
的直线 与
与 交于
交于 两点,纵坐标不为
两点,纵坐标不为 的点
的点 在直线
在直线 上,线段
上,线段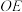 分别与线段
分别与线段 ,
, 交于
交于 两点,且
两点,且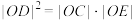 ,证明:
,证明: .
.
您最近一年使用:0次
2022/03/09
|
1108次组卷
|
3卷引用:福建省厦门第六中学2023届高三上学期期末数学试题
名校
7 . 已知椭圆 :
: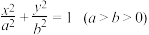 的离心率
的离心率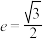 ,过椭圆的上顶点
,过椭圆的上顶点 和右顶点
和右顶点 的直线与原点
的直线与原点 的距离为
的距离为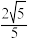 ,
,
(1)求椭圆 的方程;
的方程;
(2)是否存在直线 经过椭圆左焦点与椭圆
经过椭圆左焦点与椭圆 交于
交于 ,
, 两点,使得以线段
两点,使得以线段 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点 ?若存在,求出直线
?若存在,求出直线 方程;若不存在,请说明理由.
方程;若不存在,请说明理由.
 :
: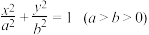 的离心率
的离心率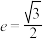 ,过椭圆的上顶点
,过椭圆的上顶点 和右顶点
和右顶点 的直线与原点
的直线与原点 的距离为
的距离为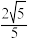 ,
,(1)求椭圆
 的方程;
的方程;(2)是否存在直线
 经过椭圆左焦点与椭圆
经过椭圆左焦点与椭圆 交于
交于 ,
, 两点,使得以线段
两点,使得以线段 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点 ?若存在,求出直线
?若存在,求出直线 方程;若不存在,请说明理由.
方程;若不存在,请说明理由.
您最近一年使用:0次
2018/03/16
|
567次组卷
|
2卷引用:福建省三明市A片区高中联盟校2017-2018学年高二上学期阶段性考试数学(文)试题



