名校
解题方法
1 . 已知 是椭圆
是椭圆 的右焦点,且
的右焦点,且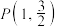 在椭圆
在椭圆 上,
上, 垂直于
垂直于 轴.
轴.
(1)求椭圆 的方程.
的方程.
(2)过点 的直线
的直线 交椭圆
交椭圆 于
于 (异于点
(异于点 )两点,
)两点, 为直线
为直线 上一点.设直线
上一点.设直线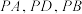 的斜率分别为
的斜率分别为 ,若
,若 ,证明:点
,证明:点 的横坐标为定值.
的横坐标为定值.
 是椭圆
是椭圆 的右焦点,且
的右焦点,且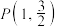 在椭圆
在椭圆 上,
上, 垂直于
垂直于 轴.
轴.(1)求椭圆
 的方程.
的方程.(2)过点
 的直线
的直线 交椭圆
交椭圆 于
于 (异于点
(异于点 )两点,
)两点, 为直线
为直线 上一点.设直线
上一点.设直线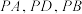 的斜率分别为
的斜率分别为 ,若
,若 ,证明:点
,证明:点 的横坐标为定值.
的横坐标为定值.
您最近一年使用:0次
2023-03-11更新
|
2267次组卷
|
13卷引用:吉林省白山市2023届高三三模联考数学试题
吉林省白山市2023届高三三模联考数学试题湖南省部分市2023届高三下学期3月大联考数学试题河南省焦作市2022-2023学年高三第二次模拟考试数学(理科)试题贵州省黔东南州2023届高三第一次适应性考试数学(文)试题贵州省黔东南州2023届高三第一次适应性考试数学(理)试题陕西省咸阳市高新一中2023届高三下学期第八次质量检测理科数学试题陕西省咸阳市高新一中2023届高三下学期第八次质量检测文科数学试题河南省焦作市2022-2023学年高三第二次模拟考试数学(文科)试题(已下线)专题16解析几何(解答题)(已下线)专题15解析几何(解答题)河北省保定市安国中学等3校2023届高三下学期3月月考数学试题辽宁省锦州市黑山县黑山中学2023届高三一模数学试题云南省曲靖市第一中学2024届高三上学期第四次月考数学试卷
解题方法
2 . 已知椭圆 和直线l:
和直线l: ,椭圆的离心率
,椭圆的离心率 ,坐标原点到直线的距离为
,坐标原点到直线的距离为 .
.
(1)求椭圆的方程;
(2)已知定点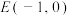 ,若直线
,若直线 与椭圆相交于C,D两点,试判断是否存在实数k,使以CD为直径的圆过定点E?若存在,求出k的值,若不存在,说明理由.
与椭圆相交于C,D两点,试判断是否存在实数k,使以CD为直径的圆过定点E?若存在,求出k的值,若不存在,说明理由.
 和直线l:
和直线l: ,椭圆的离心率
,椭圆的离心率 ,坐标原点到直线的距离为
,坐标原点到直线的距离为 .
.(1)求椭圆的方程;
(2)已知定点
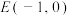 ,若直线
,若直线 与椭圆相交于C,D两点,试判断是否存在实数k,使以CD为直径的圆过定点E?若存在,求出k的值,若不存在,说明理由.
与椭圆相交于C,D两点,试判断是否存在实数k,使以CD为直径的圆过定点E?若存在,求出k的值,若不存在,说明理由.
您最近一年使用:0次
2023-02-23更新
|
707次组卷
|
3卷引用:吉林省白城市通榆县第一中学校2022-2023学年高二上学期期末数学试题
吉林省白城市通榆县第一中学校2022-2023学年高二上学期期末数学试题浙江省杭州市六县九校联盟2023-2024学年高二上学期11月期中联考数学试题(已下线)专题7-4圆锥曲线五个方程型大题归类-2
名校
解题方法
3 . 已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,过左焦点
,过左焦点 的直线
的直线 与椭圆
与椭圆 交于
交于 两点(
两点( 不在
不在 轴上),
轴上), 的周长为
的周长为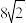 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若点 在椭圆
在椭圆 上,且
上,且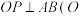 为坐标原点),求
为坐标原点),求 的取值范围.
的取值范围.
 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,过左焦点
,过左焦点 的直线
的直线 与椭圆
与椭圆 交于
交于 两点(
两点( 不在
不在 轴上),
轴上), 的周长为
的周长为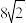 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若点
 在椭圆
在椭圆 上,且
上,且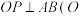 为坐标原点),求
为坐标原点),求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-02-14更新
|
754次组卷
|
7卷引用:吉林省白城市通榆县2022-2023学年高二上学期期末数学试题
名校
解题方法
4 . 已知椭圆 过点
过点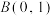 ,且离心率
,且离心率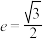 .
.
(1)求椭圆 的方程;
的方程;
(2)若斜率为 的直线
的直线 交椭圆
交椭圆 于
于 、
、 两点,交
两点,交 轴于点
轴于点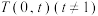 ,问是否存在实数
,问是否存在实数 使得以
使得以 为直径的圆恒过点
为直径的圆恒过点 ?若存在,求
?若存在,求 的值,若不存在,说出理由.
的值,若不存在,说出理由.
 过点
过点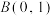 ,且离心率
,且离心率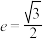 .
.(1)求椭圆
 的方程;
的方程;(2)若斜率为
 的直线
的直线 交椭圆
交椭圆 于
于 、
、 两点,交
两点,交 轴于点
轴于点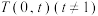 ,问是否存在实数
,问是否存在实数 使得以
使得以 为直径的圆恒过点
为直径的圆恒过点 ?若存在,求
?若存在,求 的值,若不存在,说出理由.
的值,若不存在,说出理由.
您最近一年使用:0次
名校
解题方法
5 . 如图,在平面直角坐标系,已知 ,
, 分别:
分别: 的左,右焦点.设点
的左,右焦点.设点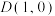 为线段
为线段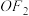 的中点.
的中点.

(1)若 为长轴
为长轴 的三等分点,求椭圆方程;
的三等分点,求椭圆方程;
(2)直线 (不与
(不与 轴重合)过点
轴重合)过点 且与椭圆
且与椭圆 交于
交于 ,
, 两点,延长
两点,延长 ,
,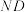 与椭圆
与椭圆 交于
交于 ,
, 两点,设直线
两点,设直线 ,
, 的斜率存在且分别为
的斜率存在且分别为 ,
, ,请将
,请将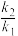 表示成关于
表示成关于 的函数,即
的函数,即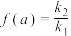 ,求
,求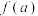 的值域.
的值域.
 ,
, 分别:
分别: 的左,右焦点.设点
的左,右焦点.设点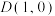 为线段
为线段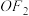 的中点.
的中点.
(1)若
 为长轴
为长轴 的三等分点,求椭圆方程;
的三等分点,求椭圆方程;(2)直线
 (不与
(不与 轴重合)过点
轴重合)过点 且与椭圆
且与椭圆 交于
交于 ,
, 两点,延长
两点,延长 ,
,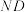 与椭圆
与椭圆 交于
交于 ,
, 两点,设直线
两点,设直线 ,
, 的斜率存在且分别为
的斜率存在且分别为 ,
, ,请将
,请将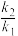 表示成关于
表示成关于 的函数,即
的函数,即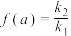 ,求
,求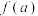 的值域.
的值域.
您最近一年使用:0次
2023-01-15更新
|
562次组卷
|
2卷引用:吉林省通化市梅河口市第五中学2022-2023学年高二下学期期初考试数学试题
名校
解题方法
6 . 已知 分别是椭圆
分别是椭圆 的左、右焦点,A是C的右顶点,
的左、右焦点,A是C的右顶点, ,P是椭圆C上一点,M,N分别为线段
,P是椭圆C上一点,M,N分别为线段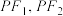 的中点,O是坐标原点,四边形OMPN的周长为4.
的中点,O是坐标原点,四边形OMPN的周长为4.
(1)求椭圆C的标准方程
(2)若不过点A的直线l与椭圆C交于D,E两点,且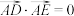 ,判断直线l是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
,判断直线l是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
 分别是椭圆
分别是椭圆 的左、右焦点,A是C的右顶点,
的左、右焦点,A是C的右顶点, ,P是椭圆C上一点,M,N分别为线段
,P是椭圆C上一点,M,N分别为线段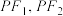 的中点,O是坐标原点,四边形OMPN的周长为4.
的中点,O是坐标原点,四边形OMPN的周长为4.(1)求椭圆C的标准方程
(2)若不过点A的直线l与椭圆C交于D,E两点,且
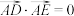 ,判断直线l是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
,判断直线l是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
您最近一年使用:0次
2023-01-02更新
|
1349次组卷
|
14卷引用:吉林省长春市第六中学2022-2023学年高二下学期4月月考数学试题
吉林省长春市第六中学2022-2023学年高二下学期4月月考数学试题山东省济宁市第一中学2022-2023学年高二上学期期末数学试题山东省烟台市烟台第一中学2022-2023学年高三上学期期末数学试题山东省临沂市费县第二中学2022-2023学年高二上学期期末数学试题山东省烟台第一中学2022-2023学年高二下学期入学摸底测试数学试题青海省西宁市海湖中学2022-2023学年高二下学期开学摸底考试数学试卷 A卷湖南省衡阳市衡阳县第四中学2022-2023学年高二平行班下学期开学模拟考试数学试题湖南省衡阳市衡阳县四中2022-2023学年高二创新班下学期开学模拟考试数学试题河南省洛阳市第八高级中学2023届高三下学期开学摸底考试理科数学试题湖北省襄阳市第四中学2022-2023学年高二下学期开学考试数学试题湖北省十堰市部分重点中学2022-2023学年高二下学期3月联考数学试题江苏省淮安市盱眙中学2023届高三七模数学试题山东省文登第一中学2024届高三上学期12月阶段测试数学试题新疆石河子第一中学2023-2024学年高二下学期3月月考数学试题
名校
解题方法
7 . 已知椭圆 :
: 过点
过点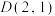 ,且该椭圆长轴长是短轴长的二倍.
,且该椭圆长轴长是短轴长的二倍.
(1)求椭圆 的方程;
的方程;
(2)设点 关于原点对称的点为
关于原点对称的点为 ,过点
,过点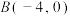 且斜率存在的直线
且斜率存在的直线 交椭圆
交椭圆 于点M,N,直线MA,NA分别交直线
于点M,N,直线MA,NA分别交直线 于点P,Q,求证
于点P,Q,求证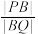 为定值.
为定值.
 :
: 过点
过点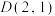 ,且该椭圆长轴长是短轴长的二倍.
,且该椭圆长轴长是短轴长的二倍.(1)求椭圆
 的方程;
的方程;(2)设点
 关于原点对称的点为
关于原点对称的点为 ,过点
,过点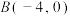 且斜率存在的直线
且斜率存在的直线 交椭圆
交椭圆 于点M,N,直线MA,NA分别交直线
于点M,N,直线MA,NA分别交直线 于点P,Q,求证
于点P,Q,求证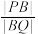 为定值.
为定值.
您最近一年使用:0次
2022-12-29更新
|
524次组卷
|
2卷引用:吉林省通化市梅河口市第五中学2022-2023学年高二上学期期末考试数学试题
8 . 已知椭圆 短轴的两个顶点与右焦点的连线构成等边三角形,直线
短轴的两个顶点与右焦点的连线构成等边三角形,直线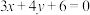 与圆
与圆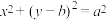 相切.
相切.
(1)求椭圆 的方程;
的方程;
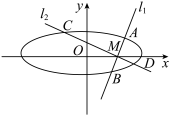
(2)过点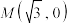 作两条互相垂直的直线
作两条互相垂直的直线 ,与椭圆
,与椭圆 分别交于
分别交于 四点,如图,求四边形
四点,如图,求四边形 的面积的取值范围.
的面积的取值范围.
 短轴的两个顶点与右焦点的连线构成等边三角形,直线
短轴的两个顶点与右焦点的连线构成等边三角形,直线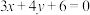 与圆
与圆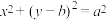 相切.
相切.
(1)求椭圆
 的方程;
的方程;(2)过点
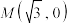 作两条互相垂直的直线
作两条互相垂直的直线 ,与椭圆
,与椭圆 分别交于
分别交于 四点,如图,求四边形
四点,如图,求四边形 的面积的取值范围.
的面积的取值范围.
您最近一年使用:0次
2022-12-03更新
|
1146次组卷
|
7卷引用:吉林省通化梅河口市第五中学2022-2023学年高三上学期期末考试数学试题
吉林省通化梅河口市第五中学2022-2023学年高三上学期期末考试数学试题四川省成都市东部新区养马高级中学2022-2023学年高二上学期期中考试数学(理)试题(已下线)专题13 圆锥曲线压轴解答题常考套路归类(精讲精练)-1(已下线)期末押题预测卷01(范围:选择性必修第一册、选择性必修第二册)-【单元测试】2022-2023学年高二数学分层训练AB卷(人教B版2019)(已下线)专题04 圆锥曲线经典题型全归纳(1)山东省青岛市第十七中学2022-2023学年高二上学期期末数学试题(已下线)高二数学开学摸底考01(新高考地区)-2023-2024学年高中下学期开学摸底考试卷
9 . 已知椭圆 的左顶点为
的左顶点为 ,点
,点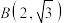 在椭圆
在椭圆 上,且
上,且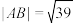 .
.
(1)求椭圆 的标准方程.
的标准方程.
(2)设过点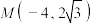 的直线
的直线 与椭圆
与椭圆 交于
交于 (异于
(异于 两点)两点,直线
两点)两点,直线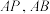 ,
, 分别与
分别与 轴交于
轴交于 三点.证明:
三点.证明: 是线段
是线段 的中点.
的中点.
 的左顶点为
的左顶点为 ,点
,点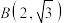 在椭圆
在椭圆 上,且
上,且 .
.(1)求椭圆
 的标准方程.
的标准方程.(2)设过点
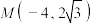 的直线
的直线 与椭圆
与椭圆 交于
交于 (异于
(异于 两点)两点,直线
两点)两点,直线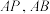 ,
, 分别与
分别与 轴交于
轴交于 三点.证明:
三点.证明: 是线段
是线段 的中点.
的中点.
您最近一年使用:0次
2022-11-16更新
|
421次组卷
|
3卷引用:吉林省吉林市等2地2022-2023学年高二上学期期中联考数学试题
名校
解题方法
10 . 已知椭圆C: 的左、右顶点分别为A、B,上顶点M与左右顶点连线MA,MB的斜率乘积为
的左、右顶点分别为A、B,上顶点M与左右顶点连线MA,MB的斜率乘积为 ,焦距为4.
,焦距为4.
(1)求椭圆C的方程;
(2)设点P为椭圆上异于A,B的点,直线AP与y轴的交点为Q,过坐标原点O作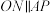 交椭圆于N点,试探究
交椭圆于N点,试探究 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
 的左、右顶点分别为A、B,上顶点M与左右顶点连线MA,MB的斜率乘积为
的左、右顶点分别为A、B,上顶点M与左右顶点连线MA,MB的斜率乘积为 ,焦距为4.
,焦距为4.(1)求椭圆C的方程;
(2)设点P为椭圆上异于A,B的点,直线AP与y轴的交点为Q,过坐标原点O作
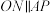 交椭圆于N点,试探究
交椭圆于N点,试探究 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
您最近一年使用:0次
2022-11-14更新
|
796次组卷
|
3卷引用:吉林省实验中学2022-2023学年高二上学期期中数学试题



