1 . 设过点 与直线
与直线 相切的动圆圆心的轨迹为
相切的动圆圆心的轨迹为 ,不过坐标原点
,不过坐标原点 的直线
的直线 与曲线
与曲线 交于
交于 、
、 两点,且
两点,且 .
.
(1)求曲线 的方程;
的方程;
(2)求证:直线 过定点;
过定点;
(3)若 、
、 两点到
两点到 的距离相差为6,求
的距离相差为6,求 的值.
的值.
 与直线
与直线 相切的动圆圆心的轨迹为
相切的动圆圆心的轨迹为 ,不过坐标原点
,不过坐标原点 的直线
的直线 与曲线
与曲线 交于
交于 、
、 两点,且
两点,且 .
.(1)求曲线
 的方程;
的方程;(2)求证:直线
 过定点;
过定点;(3)若
 、
、 两点到
两点到 的距离相差为6,求
的距离相差为6,求 的值.
的值.
您最近一年使用:0次
解题方法
2 . 已知曲线C上任意点到点F(1,0)距离比到直线x+2=0的距离少1.
(1)求C的方程,并说明C为何种曲线;
(2)已知A(1,2)及曲线C上的两点B和D,直线AB,AD的斜率分别为k1,k2,且k1+k2=1,求证:直线BD经过定点.
(1)求C的方程,并说明C为何种曲线;
(2)已知A(1,2)及曲线C上的两点B和D,直线AB,AD的斜率分别为k1,k2,且k1+k2=1,求证:直线BD经过定点.
您最近一年使用:0次
名校
解题方法
3 . 已知抛物线 上一点
上一点 到焦点
到焦点 的距离为4.
的距离为4.
(1)求抛物线 的标准方程;
的标准方程;
(2)过焦点 的直线
的直线 与抛物线
与抛物线 交于不同的两点
交于不同的两点 ,
, ,
, 为坐标原点,设直线
为坐标原点,设直线 ,
, 的斜率分别为
的斜率分别为 ,
, ,求证:
,求证: 为定值.
为定值.
 上一点
上一点 到焦点
到焦点 的距离为4.
的距离为4.(1)求抛物线
 的标准方程;
的标准方程;(2)过焦点
 的直线
的直线 与抛物线
与抛物线 交于不同的两点
交于不同的两点 ,
, ,
, 为坐标原点,设直线
为坐标原点,设直线 ,
, 的斜率分别为
的斜率分别为 ,
, ,求证:
,求证: 为定值.
为定值.
您最近一年使用:0次
2022-12-20更新
|
617次组卷
|
5卷引用:四川省泸县第一中学2022-2023学年高二上学期期末考试数学(理)试题
解题方法
4 . 抛物线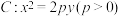 的焦点
的焦点 是椭圆
是椭圆 的一个焦点.
的一个焦点.
(1)求 的准线方程;
的准线方程;
(2)若 是直线
是直线 上的一动点,过
上的一动点,过 向
向 作两条切线,切点为M,N,试探究直线MN是否过定点?若是,请求出定点,若否,请说明理由.
作两条切线,切点为M,N,试探究直线MN是否过定点?若是,请求出定点,若否,请说明理由.
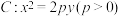 的焦点
的焦点 是椭圆
是椭圆 的一个焦点.
的一个焦点.(1)求
 的准线方程;
的准线方程;(2)若
 是直线
是直线 上的一动点,过
上的一动点,过 向
向 作两条切线,切点为M,N,试探究直线MN是否过定点?若是,请求出定点,若否,请说明理由.
作两条切线,切点为M,N,试探究直线MN是否过定点?若是,请求出定点,若否,请说明理由.
您最近一年使用:0次
解题方法
5 . 抛物线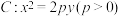 的焦点
的焦点 是椭圆
是椭圆 的一个焦点.
的一个焦点.
(1)求 的准线方程;
的准线方程;
(2)若 是直线
是直线 上的一动点,过
上的一动点,过 向
向 作两条切线,切点为M,N,当点
作两条切线,切点为M,N,当点 到直线
到直线 的距离最大值时,求点
的距离最大值时,求点 的坐标.
的坐标.
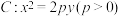 的焦点
的焦点 是椭圆
是椭圆 的一个焦点.
的一个焦点.(1)求
 的准线方程;
的准线方程;(2)若
 是直线
是直线 上的一动点,过
上的一动点,过 向
向 作两条切线,切点为M,N,当点
作两条切线,切点为M,N,当点 到直线
到直线 的距离最大值时,求点
的距离最大值时,求点 的坐标.
的坐标.
您最近一年使用:0次
名校
解题方法
6 . 已知拋物线 的焦点为
的焦点为 ,过点
,过点 且斜率为
且斜率为 的直线
的直线 交
交 于
于 两点.当
两点.当 时,
时,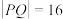 .
.
(1)求 的方程;
的方程;
(2)若 关于
关于 轴的对称点为
轴的对称点为 ,当
,当 变化时,求证:直线
变化时,求证:直线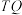 过定点,并求该定点坐标.
过定点,并求该定点坐标.
 的焦点为
的焦点为 ,过点
,过点 且斜率为
且斜率为 的直线
的直线 交
交 于
于 两点.当
两点.当 时,
时,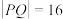 .
.(1)求
 的方程;
的方程;(2)若
 关于
关于 轴的对称点为
轴的对称点为 ,当
,当 变化时,求证:直线
变化时,求证:直线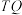 过定点,并求该定点坐标.
过定点,并求该定点坐标.
您最近一年使用:0次
2022-07-20更新
|
341次组卷
|
5卷引用:四川省资阳市2021-2022学年高二下学期期末质量检测数学(理)试题
四川省资阳市2021-2022学年高二下学期期末质量检测数学(理)试题四川省资阳市2021-2022学年高二下学期期末数学文科试题四川省泸县第四中学2022-2023学年高二下学期开学考试数学(理)试题江苏省南京外国语学校2023-2024学年高二上学期10月月考数学试题(已下线)专题3-6 抛物线综合大题归类(讲+练)-【巅峰课堂】2023-2024学年高二数学热点题型归纳与培优练(人教A版2019选择性必修第一册)
7 . 在平面直角坐标系xOy中,已知点 ,点P到点F的距离比点P到直线
,点P到点F的距离比点P到直线 的距离小1,记P的轨迹为C.
的距离小1,记P的轨迹为C.
(1)求曲线C的方程;
(2)在直线 上任取一点M,过M作曲线C的切线
上任取一点M,过M作曲线C的切线 ,切点分别为A、B,求证直线AB过定点.
,切点分别为A、B,求证直线AB过定点.
 ,点P到点F的距离比点P到直线
,点P到点F的距离比点P到直线 的距离小1,记P的轨迹为C.
的距离小1,记P的轨迹为C.(1)求曲线C的方程;
(2)在直线
 上任取一点M,过M作曲线C的切线
上任取一点M,过M作曲线C的切线 ,切点分别为A、B,求证直线AB过定点.
,切点分别为A、B,求证直线AB过定点.
您最近一年使用:0次
解题方法
8 . 在平面直角坐标系xOy中,已知点 ,点P到点F的距离比点P到x轴的距离大2,记P的轨迹为C.
,点P到点F的距离比点P到x轴的距离大2,记P的轨迹为C.
(1)求C的方程;
(2)A、B是C上的两点,直线OA、OB的斜率分别为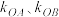 且
且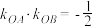 ,求证直线
,求证直线 过定点.
过定点.
 ,点P到点F的距离比点P到x轴的距离大2,记P的轨迹为C.
,点P到点F的距离比点P到x轴的距离大2,记P的轨迹为C.(1)求C的方程;
(2)A、B是C上的两点,直线OA、OB的斜率分别为
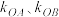 且
且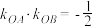 ,求证直线
,求证直线 过定点.
过定点.
您最近一年使用:0次
2022-07-15更新
|
1233次组卷
|
4卷引用:四川省遂宁市2021-2022学年高二下学期期末数学文科试题
解题方法
9 . 设抛物线 上位于第一象限的点M与焦点F的距离为
上位于第一象限的点M与焦点F的距离为 ,点M到x轴的距离为2p,直线l与抛物线相交于A,B两点,且
,点M到x轴的距离为2p,直线l与抛物线相交于A,B两点,且 .
.
(1)求抛物线的方程和点M的坐标;
(2)求证:直线l恒过定点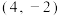 .
.
 上位于第一象限的点M与焦点F的距离为
上位于第一象限的点M与焦点F的距离为 ,点M到x轴的距离为2p,直线l与抛物线相交于A,B两点,且
,点M到x轴的距离为2p,直线l与抛物线相交于A,B两点,且 .
.(1)求抛物线的方程和点M的坐标;
(2)求证:直线l恒过定点
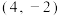 .
.
您最近一年使用:0次
解题方法
10 . 设抛物线 位于第一象限的点M与焦点F的距离为
位于第一象限的点M与焦点F的距离为 ,点M到x轴的距离为2p,直线l与抛物线相交于A,B两点,且
,点M到x轴的距离为2p,直线l与抛物线相交于A,B两点,且 .
.
(1)求抛物线的方程和点M的坐标;
(2)探究直线l是否恒过定点,并说明理由.
 位于第一象限的点M与焦点F的距离为
位于第一象限的点M与焦点F的距离为 ,点M到x轴的距离为2p,直线l与抛物线相交于A,B两点,且
,点M到x轴的距离为2p,直线l与抛物线相交于A,B两点,且 .
.(1)求抛物线的方程和点M的坐标;
(2)探究直线l是否恒过定点,并说明理由.
您最近一年使用:0次



