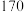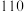名校
1 . 下列说法正确的是( )
A.设随机变量 的均值为 的均值为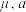 是不等于 是不等于 的常数,则 的常数,则 相对于 相对于 的偏离程度小于 的偏离程度小于 相对于 相对于 的偏离程度(偏离程度用差的平方表示) 的偏离程度(偏离程度用差的平方表示) |
B.若一组数据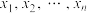 的方差为0,则所有数据 的方差为0,则所有数据 都相同 都相同 |
C.用决定系数 比较两个回归模型的拟合效果时, 比较两个回归模型的拟合效果时, 越小,残差平方和越小,模型拟合效果越好 越小,残差平方和越小,模型拟合效果越好 |
D.在对两个分类变量进行 独立性检验时,如果列联表中所有数据都扩大为原来的10倍,在相同的检验标准下,再去判断两变量的关联性时,结论不会发生改变 独立性检验时,如果列联表中所有数据都扩大为原来的10倍,在相同的检验标准下,再去判断两变量的关联性时,结论不会发生改变 |
您最近半年使用:0次
7日内更新
|
413次组卷
|
2卷引用:云南三校2024届高三高考备考实用性联考卷(七)数学试卷
解题方法
2 . 某网络购物平台专营店统计了某年2月15日至19日这5天在该店购物的人数 (单位:人)的数据如下表:
(单位:人)的数据如下表:
(1)根据表中数据,建立 关于
关于 的一元线性回归模型,并根据该回归模型预测当年2月21日在该店购物的人数(人数用四舍五入法取整数);
的一元线性回归模型,并根据该回归模型预测当年2月21日在该店购物的人数(人数用四舍五入法取整数);
(2)为了了解参加网购人群的年龄分布,该店随机抽取了200人进行问卷调查.得到如下所示不完整的 列联表:
列联表:
将列联表补充完整,并依据表中数据及小概率值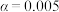 的独立性检验,能否认为“参与网上购物”与“年龄”有关.
的独立性检验,能否认为“参与网上购物”与“年龄”有关.
附:回归直线的斜率和截距的最小二乘估计公式分别为
 (单位:人)的数据如下表:
(单位:人)的数据如下表:日期 | 2月15日 | 2月16日 | 2月17日 | 2月18日 | 2月19日 |
日期代号 | 1 | 2 | 3 | 4 | 5 |
购物人数 | 77 | 84 | 93 | 96 | 100 |
 关于
关于 的一元线性回归模型,并根据该回归模型预测当年2月21日在该店购物的人数(人数用四舍五入法取整数);
的一元线性回归模型,并根据该回归模型预测当年2月21日在该店购物的人数(人数用四舍五入法取整数);(2)为了了解参加网购人群的年龄分布,该店随机抽取了200人进行问卷调查.得到如下所示不完整的
 列联表:
列联表:| 年龄 | 不低于40岁 | 低于40岁 | 合计 |
参与过网上购物 | 30 | 150 | |
未参与过网上购物 | 30 | ||
合计 | 200 |
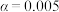 的独立性检验,能否认为“参与网上购物”与“年龄”有关.
的独立性检验,能否认为“参与网上购物”与“年龄”有关.附:回归直线的斜率和截距的最小二乘估计公式分别为

 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
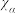 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近半年使用:0次
名校
解题方法
3 . 某地区响应“节能减排,低碳生活”的号召,开展系列的措施控制碳排放.环保部门收集到近5年内新增碳排放数量,如下表所示,其中 为年份代号,
为年份代号, (单位:万吨)代表新增碳排放量.
(单位:万吨)代表新增碳排放量.
(1)请计算并用相关系数 的数值说明
的数值说明 与
与 之间的线性相关性的强弱(保留小数点后两位);
之间的线性相关性的强弱(保留小数点后两位);
(2)求 关于
关于 的线性回归方程,并据此估计该地区2024年的新增碳排放数量.
的线性回归方程,并据此估计该地区2024年的新增碳排放数量.
参考数据: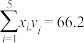 ,
,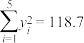 ,
,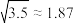 ,
,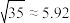 .
.
参考公式:对于一组数据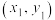 ,
,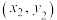 ,…,
,…,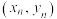 ,其回归直线的斜率和截距的最小二乘法估计公式,相关系数
,其回归直线的斜率和截距的最小二乘法估计公式,相关系数 的公式分别为
的公式分别为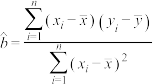 ,
, ,
,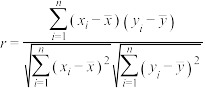
 为年份代号,
为年份代号, (单位:万吨)代表新增碳排放量.
(单位:万吨)代表新增碳排放量.年份 | 2019 | 2020 | 2021 | 2022 | 2023 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
新增碳排放 | 6.1 | 5.2 | 4.9 | 4 | 3.8 |
 的数值说明
的数值说明 与
与 之间的线性相关性的强弱(保留小数点后两位);
之间的线性相关性的强弱(保留小数点后两位);(2)求
 关于
关于 的线性回归方程,并据此估计该地区2024年的新增碳排放数量.
的线性回归方程,并据此估计该地区2024年的新增碳排放数量.参考数据:
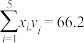 ,
,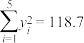 ,
,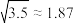 ,
,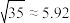 .
.参考公式:对于一组数据
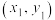 ,
,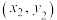 ,…,
,…,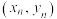 ,其回归直线的斜率和截距的最小二乘法估计公式,相关系数
,其回归直线的斜率和截距的最小二乘法估计公式,相关系数 的公式分别为
的公式分别为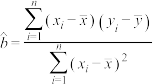 ,
, ,
,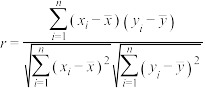
您最近半年使用:0次
名校
4 . 为了了解居家学习期间性别因素是否对学生体育锻炼的经常性有影响,某校随机抽取了 名学生进行调查,按照性别和体育锻炼情况整理出如下的
名学生进行调查,按照性别和体育锻炼情况整理出如下的 列联表:
列联表:
常用的小概率值和相应的临界值如下表:
注: 独立性检验中,
独立性检验中, ,
, .
.
根据这些数据,判断下列说法正确的是( )
 名学生进行调查,按照性别和体育锻炼情况整理出如下的
名学生进行调查,按照性别和体育锻炼情况整理出如下的 列联表:
列联表:性别 | 锻炼情况 | 合计 | |
不经常 | 经常 | ||
女生/人 | 5 | 30 | 35 |
男生/人 | 5 | 10 | 15 |
合计/人 | 10 | 40 | 50 |
| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 独立性检验中,
独立性检验中, ,
, .
.根据这些数据,判断下列说法正确的是( )
| A.依据频率稳定于概率的原理,可以认为性别对体育锻炼的经常性没有影响 |
| B.依据频率稳定于概率的原理,可以认为性别对体育锻炼的经常性有影响 |
C.根据小概率值 的独立性检验,可以认为性别对体育锻炼的经常性有影响,这个推断犯错误的概率不超过0.05 的独立性检验,可以认为性别对体育锻炼的经常性有影响,这个推断犯错误的概率不超过0.05 |
D.根据小概率值 的独立性检验,没有充分证据推断性别对体育锻炼的经常性有影响,因此可以认为性别对体育锻炼的经常性没有影响 的独立性检验,没有充分证据推断性别对体育锻炼的经常性有影响,因此可以认为性别对体育锻炼的经常性没有影响 |
您最近半年使用:0次
名校
解题方法
5 . 某大学保卫处随机抽取该校1000名大学生对该校学生进出校园管理制度的态度进行了问卷调查,结果见下表:
(1)根据小概率值 的独立性检验,分析该校大学生赞成学生进出校园管理制度与学生的性别是否有关;
的独立性检验,分析该校大学生赞成学生进出校园管理制度与学生的性别是否有关;
(2)为答谢参与问卷调查的同学,参与本次问卷调查的同学每人可以抽一次奖,获奖结果及概率如下:
若甲、乙两名同学准备参加抽奖,他们的获奖结果相互独立,记两人获得奖金的总金额为 (单位:元),求
(单位:元),求 的数学期望
的数学期望 .
.
附: ,其中
,其中 .
.
| 男生(单位:人) | 女生(单位:人) | 总计 | |
| 赞成 | 400 | 300 | 700 |
| 不赞成 | 100 | 200 | 300 |
| 总计 | 500 | 500 | 1000 |
 的独立性检验,分析该校大学生赞成学生进出校园管理制度与学生的性别是否有关;
的独立性检验,分析该校大学生赞成学生进出校园管理制度与学生的性别是否有关;(2)为答谢参与问卷调查的同学,参与本次问卷调查的同学每人可以抽一次奖,获奖结果及概率如下:
| 奖金(单位:元) | 0 | 10 | 20 |
| 获奖概率 |  |  |  |
 (单位:元),求
(单位:元),求 的数学期望
的数学期望 .
.附:
 ,其中
,其中 .
. | 0.15 | 0.10 | 0.05 | 0.010 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
您最近半年使用:0次
2024-04-04更新
|
518次组卷
|
3卷引用:云南省2024届高三第一次高中毕业生复习统一检测数学试题
名校
6 . 近两年来,自行车的市场占有率在不断提升,随着人们的健康意识不断增强,骑自行车不仅仅是人们出行的交通方式,也渐渐成为一种新颖的运动,越来越多的人加入了骑行一族.在某地区随机调查了100位自行车骑行者的年龄分布情况,得到如图所示的样本数据频率分布直方图.
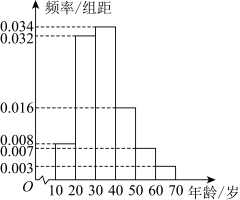
(1)数据显示,该地区年龄在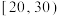 岁内的人口占比为12%,该地区自行车骑行率约为13%,从该地区任选一人,已知此人年龄在
岁内的人口占比为12%,该地区自行车骑行率约为13%,从该地区任选一人,已知此人年龄在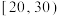 内,求此人是自行车骑行者的概率;
内,求此人是自行车骑行者的概率;
(2)对这100位自行车骑行者进行统计,骑行频率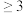 次/周的共有70人,其中年龄在40岁以下的占80%.请完成以下
次/周的共有70人,其中年龄在40岁以下的占80%.请完成以下 列联表,并根据小概率值
列联表,并根据小概率值 的独立性检验,判断骑行频率与年龄是否有关联.
的独立性检验,判断骑行频率与年龄是否有关联.
年龄
附: ,其中
,其中 .
.

(1)数据显示,该地区年龄在
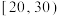 岁内的人口占比为12%,该地区自行车骑行率约为13%,从该地区任选一人,已知此人年龄在
岁内的人口占比为12%,该地区自行车骑行率约为13%,从该地区任选一人,已知此人年龄在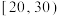 内,求此人是自行车骑行者的概率;
内,求此人是自行车骑行者的概率;(2)对这100位自行车骑行者进行统计,骑行频率
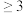 次/周的共有70人,其中年龄在40岁以下的占80%.请完成以下
次/周的共有70人,其中年龄在40岁以下的占80%.请完成以下 列联表,并根据小概率值
列联表,并根据小概率值 的独立性检验,判断骑行频率与年龄是否有关联.
的独立性检验,判断骑行频率与年龄是否有关联.年龄
| 骑行频率 | 年龄 | 合计 | |
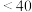 岁 岁 | 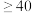 岁 岁 | ||
 次/周 次/周 | |||
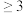 次/周 次/周 | |||
| 合计 | |||
 ,其中
,其中 .
. | 0.050 | 0.010 | 0.001 |
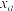 | 3.841 | 6.635 | 10.828 |
您最近半年使用:0次
7 . 已知某种商品的广告费支出 (单位:万元)与销售额
(单位:万元)与销售额 (单位:万元)之间有如下表对应数据:
(单位:万元)之间有如下表对应数据:
根据表中数据得到 关于
关于 的经验回归方程为
的经验回归方程为 ,则当
,则当 时,残差为
时,残差为__________ .(残差 观测值-预测值)
观测值-预测值)
 (单位:万元)与销售额
(单位:万元)与销售额 (单位:万元)之间有如下表对应数据:
(单位:万元)之间有如下表对应数据: | 1 | 3 | 4 | 5 | 7 |
 | 15 | 20 | 30 | 40 | 45 |
 关于
关于 的经验回归方程为
的经验回归方程为 ,则当
,则当 时,残差为
时,残差为 观测值-预测值)
观测值-预测值)
您最近半年使用:0次
名校
8 . 色差和色度是衡量玩具质量优劣的重要指标,已知该产品的色度 和色差
和色差 之间满足线性相关关系,且
之间满足线性相关关系,且 ,现有一对测量数据为(30,22.8),则该数据的残差为( )
,现有一对测量数据为(30,22.8),则该数据的残差为( )
 和色差
和色差 之间满足线性相关关系,且
之间满足线性相关关系,且 ,现有一对测量数据为(30,22.8),则该数据的残差为( )
,现有一对测量数据为(30,22.8),则该数据的残差为( )| A.0.6 | B.0.4 | C.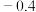 | D.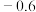 |
您最近半年使用:0次
2024-03-03更新
|
547次组卷
|
5卷引用:云南省曲靖市第一中学2023-2024学年高二下学期第一次阶段性考试(3月月考)数学试题
云南省曲靖市第一中学2023-2024学年高二下学期第一次阶段性考试(3月月考)数学试题黑龙江省双鸭山市第一中学2023-2024学年高二下学期开学考试数学试题(已下线)8.2 一元线性回归模型及其应用(分层练习,7大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)第9章 统计单元综合能力测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)8.2.1一元线性回归模型+8.2.2一元线性回归模型 第二练 强化考点训练
名校
9 . 为了研究体育锻炼对某年龄段的人患某种慢性病的影响,某人随机走访了 个该年龄段的人,得到的数据如下:
个该年龄段的人,得到的数据如下:
(1)定义分类变量 、
、 如下:
如下: ,
,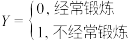 ,以频率估计概率,求条件概率
,以频率估计概率,求条件概率 与
与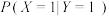 的值;
的值;
(2)根据小概率值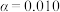 的独立性检验,分析经常进行体育锻炼是否对患该种慢性病有影响.
的独立性检验,分析经常进行体育锻炼是否对患该种慢性病有影响.
附:
 个该年龄段的人,得到的数据如下:
个该年龄段的人,得到的数据如下:慢性病 | 体育锻炼 | 合计 | |
经常 | 不经常 | ||
未患病 |
|
|
|
患病 |
|
|
|
合计 |
|
|
|
 、
、 如下:
如下: ,
,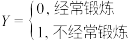 ,以频率估计概率,求条件概率
,以频率估计概率,求条件概率 与
与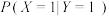 的值;
的值;(2)根据小概率值
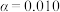 的独立性检验,分析经常进行体育锻炼是否对患该种慢性病有影响.
的独立性检验,分析经常进行体育锻炼是否对患该种慢性病有影响.附:

|
|
|
|
|
|
|
|
|
|
|
|
您最近半年使用:0次
2024-03-01更新
|
265次组卷
|
2卷引用:云南省昆明市第十四中学2023-2024学年高二下学期4月月考数学试卷
名校
10 . 全国“村BA”篮球赛点燃了全民的运动激情,深受广大球迷的喜爱.每支球队都有一个或几个主力队员,现有一支“村BA”球队,其中甲球员是其主力队员,经统计该球队在某个赛季的所有比赛中,甲球员是否上场时该球队的胜负情况如表.
(1)完成 列联表,并判断依据小概率值
列联表,并判断依据小概率值 的独立性检验,能否认为球队的胜负与甲球员是否上场有关;
的独立性检验,能否认为球队的胜负与甲球员是否上场有关;
(2)由于队员的不同,甲球员主打的位置会进行调整,根据以往的数据统计,甲球员上场时,打前锋、中锋、后卫的概率分别为0.3,0.5,0.2,相应球队赢球的概率分别为0.7,0.8,0.6.
(i)当甲球员上场参加比赛时,求球队赢球的概率;
(ii)当甲球员上场参加比赛时,在球队赢了某场比赛的条件下,求甲球员打中锋的概率.(精确到0.01)
附: ,
, .
.
甲球员是否上场 | 球队的胜负情况 | 合计 | |
胜 | 负 | ||
上场 | 40 | 45 | |
未上场 | 3 | ||
合计 | 42 | ||
 列联表,并判断依据小概率值
列联表,并判断依据小概率值 的独立性检验,能否认为球队的胜负与甲球员是否上场有关;
的独立性检验,能否认为球队的胜负与甲球员是否上场有关;(2)由于队员的不同,甲球员主打的位置会进行调整,根据以往的数据统计,甲球员上场时,打前锋、中锋、后卫的概率分别为0.3,0.5,0.2,相应球队赢球的概率分别为0.7,0.8,0.6.
(i)当甲球员上场参加比赛时,求球队赢球的概率;
(ii)当甲球员上场参加比赛时,在球队赢了某场比赛的条件下,求甲球员打中锋的概率.(精确到0.01)
附:
 ,
, .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
您最近半年使用:0次