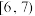名校
解题方法
1 . 画糖是一种以糖为材料在石板上进行造型的民间艺术,常见于公园与旅游景点.某师傅制作了一种新造型糖画,为了合理定价,先进行试销售,其单价x(元)与销量y(个)相关数据如表:
(1)已知销量y与单价x具有线性相关关系,求y关于x的线性回归方程;
(2)若该新造型糖画每个的成本为5.7元,要使得进入售卖时利润最大,请利用所求出的线性回归方程确定单价应该定为多少元?(结果保留到整数)
参考公式:线性回归方程y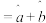 x中斜率和截距最小二乘法估计计算公式:
x中斜率和截距最小二乘法估计计算公式: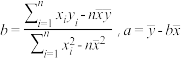 .参考数据:
.参考数据: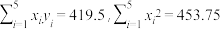 .
.
| 单价x(元) | 8.5 | 9 | 9.5 | 10 | 10.5 |
| 销量y(个) | 12 | 11 | 9 | 7 | 6 |
(2)若该新造型糖画每个的成本为5.7元,要使得进入售卖时利润最大,请利用所求出的线性回归方程确定单价应该定为多少元?(结果保留到整数)
参考公式:线性回归方程y
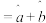 x中斜率和截距最小二乘法估计计算公式:
x中斜率和截距最小二乘法估计计算公式: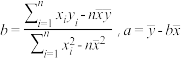 .参考数据:
.参考数据: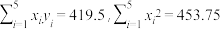 .
.
您最近一年使用:0次
2020-02-12更新
|
195次组卷
|
2卷引用:江西省赣州市2019-2020学年高二上学期期中数学(理)试题
2 . 某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
(1)求回归直线方程 ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润 销售收入
销售收入 成本)(附:对于一组数据
成本)(附:对于一组数据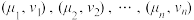 ,其回归直线
,其回归直线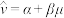 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: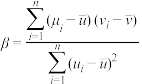 ,
, ),
),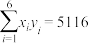 ,
,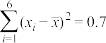
单价 元 元 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 件 件 | 100 | 94 | 93 | 90 | 85 | 78 |
 ;
;(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润
 销售收入
销售收入 成本)(附:对于一组数据
成本)(附:对于一组数据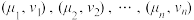 ,其回归直线
,其回归直线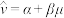 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: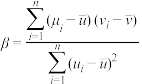 ,
, ),
),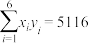 ,
,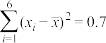
您最近一年使用:0次
名校
解题方法
3 . 某公司对某产品进行市场调研,获得了该产品的定价x(单位:万元/吨)和一天的销售量y(单位:吨)的一组数据,制作了如下的数据统计表,并作出了散点图.
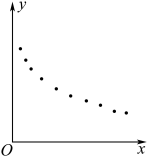
表中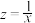 ,
, ,
,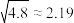 .
.
(1)根据散点图判断, 与
与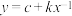 哪一个更适合作为y关于x的经验回归方程模型:(给出判断即可,不必说明理由)
哪一个更适合作为y关于x的经验回归方程模型:(给出判断即可,不必说明理由)
(2)根据(1)的判断结果,试建立y关于x的经验回归方程;
(3)若生产1吨该产品的成本为0.20万元,依据(2)的经验回归方程,预计定价为多少时,该产品一天的利润最大,并求此时的月利润.(每月按30天计算,计算结果保留两位小数)
参考公式:经验回归方程 ,其中
,其中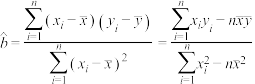 ,
, .
.

 | 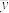 |  | 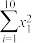 | 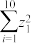 | 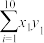 | 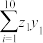 |
| 0.33 | 10 | 3 | 0.164 | 100 | 68 | 350 |
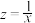 ,
, ,
,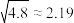 .
.(1)根据散点图判断,
 与
与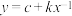 哪一个更适合作为y关于x的经验回归方程模型:(给出判断即可,不必说明理由)
哪一个更适合作为y关于x的经验回归方程模型:(给出判断即可,不必说明理由)(2)根据(1)的判断结果,试建立y关于x的经验回归方程;
(3)若生产1吨该产品的成本为0.20万元,依据(2)的经验回归方程,预计定价为多少时,该产品一天的利润最大,并求此时的月利润.(每月按30天计算,计算结果保留两位小数)
参考公式:经验回归方程
 ,其中
,其中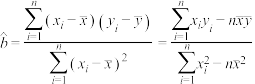 ,
, .
.
您最近一年使用:0次
2022-09-29更新
|
1198次组卷
|
12卷引用:江西省2021届高三下学期二模数学(文)试题
江西省2021届高三下学期二模数学(文)试题(已下线)文科数学-2021年高考考前20天终极冲刺攻略+(三)(6月2日)山东省济宁市第一中学2021-2022学年高三上学期开学学情考试数学试题(已下线)专题06 非线性回归方程-【解题思路培养】2022年高考数学一轮复习解答题拿分秘籍(全国通用版)四川省成都市郫都区2021-2022学年高三上学期阶段性检测(二)理科数学试题四川省成都市郫都区2021-2022学年高三上学期阶段性检测(二)文科数学试题(已下线)专题10-1 统计大题:线性和非线性回归与残差-2022年高考数学毕业班二轮热点题型归纳与变式演练(全国通用)福建省福州延安中学2021-2022学年高二下学期期末质量检测数学试题(已下线)第03讲 成对数据的统计分析 (高频考点,精讲)-1内蒙古通辽市重点校2022-2023学年高二上学期期末检测理科数学试题辽宁省大连市第一中学2022-2023学年高二下学期4月月考数学试题辽宁省大连市第八中学2021-2022学年高二下学期6月月考数学试题
4 . 为了解某地区某种农产品的年产量 (单位:吨)对价格
(单位:吨)对价格 (单位:千元/吨)和利润
(单位:千元/吨)和利润 的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表:
已知 和
和 具有线性相关关系.
具有线性相关关系.
(1)求 关于
关于 的线性回归方程
的线性回归方程 ;
;
(2)若每吨该农产品的成本为2.2千元,假设该农产品可全部卖出,预测当年产量为多少吨时,年利润 取到最大值?
取到最大值?
参考公式: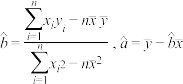 .
.
 (单位:吨)对价格
(单位:吨)对价格 (单位:千元/吨)和利润
(单位:千元/吨)和利润 的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表: | 1 | 2 | 3 | 4 | 5 |
 | 8 | 6 | 5 | 4 | 2 |
 和
和 具有线性相关关系.
具有线性相关关系.(1)求
 关于
关于 的线性回归方程
的线性回归方程 ;
;(2)若每吨该农产品的成本为2.2千元,假设该农产品可全部卖出,预测当年产量为多少吨时,年利润
 取到最大值?
取到最大值?参考公式:
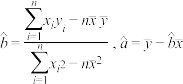 .
.
您最近一年使用:0次
名校
解题方法
5 . 某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2019年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示:
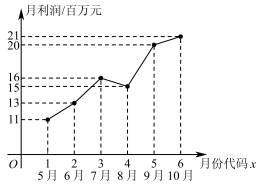
(1)由折线图可以看出,可用线性回归模型拟合月利润 (单位:百万元)与月份代码
(单位:百万元)与月份代码 之间的关系,求
之间的关系,求 关于
关于 的线性回归方程,并预测该公司2020年4月份的利润;
的线性回归方程,并预测该公司2020年4月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有A,B两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,但新材料的不稳定性会导致材料的使用寿命不同,现对A,B两种型号的新型材料对应的产品各100件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
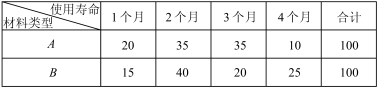
经甲公司测算平均每件新型材料每月可以带来6万元收入入,不考虑除采购成本之外的其他成本,A型号材料每件的采购成本为10万元,B型号材料每件的采购成本为12万元.假设每件新型材料的使用寿命都是整月数,且以频率作为每件新型材料使用寿命的概率,如果你是甲公司的负责人,以每件新型材料产生利润的平均值为决策依据,你会选择采购哪款新型材料?
参考数据: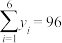 ,
,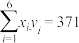 .
.
参考公式:回归直线方程 ,其中
,其中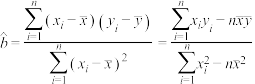 .
.

(1)由折线图可以看出,可用线性回归模型拟合月利润
 (单位:百万元)与月份代码
(单位:百万元)与月份代码 之间的关系,求
之间的关系,求 关于
关于 的线性回归方程,并预测该公司2020年4月份的利润;
的线性回归方程,并预测该公司2020年4月份的利润;(2)甲公司新研制了一款产品,需要采购一批新型材料,现有A,B两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,但新材料的不稳定性会导致材料的使用寿命不同,现对A,B两种型号的新型材料对应的产品各100件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:

经甲公司测算平均每件新型材料每月可以带来6万元收入入,不考虑除采购成本之外的其他成本,A型号材料每件的采购成本为10万元,B型号材料每件的采购成本为12万元.假设每件新型材料的使用寿命都是整月数,且以频率作为每件新型材料使用寿命的概率,如果你是甲公司的负责人,以每件新型材料产生利润的平均值为决策依据,你会选择采购哪款新型材料?
参考数据:
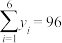 ,
,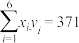 .
.参考公式:回归直线方程
 ,其中
,其中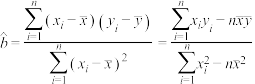 .
.
您最近一年使用:0次
2020-05-22更新
|
549次组卷
|
3卷引用:江西省南昌市第二中学2019-2020学年高三5月模拟数学(文)试题
名校
6 . 某书店销售刚刚上市的某高二数学单元测试卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如下数据:
(1)求试销 天的销量的方差和
天的销量的方差和 关于
关于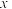 的回归直线方程;
的回归直线方程;
附: .
.
(2)预计以后的销售中,销量与单价服从上题中的回归直线方程,已知每册单元测试卷的成本是10元,为了获得最大利润,该单元测试卷的单价应定为多少元?
| 单价x/元 | 18 | 19 | 20 | 21 | 22 |
| 销量y/册 | 61 | 56 | 50 | 48 | 45 |
(1)求试销
 天的销量的方差和
天的销量的方差和 关于
关于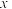 的回归直线方程;
的回归直线方程;附:
 .
.(2)预计以后的销售中,销量与单价服从上题中的回归直线方程,已知每册单元测试卷的成本是10元,为了获得最大利润,该单元测试卷的单价应定为多少元?
您最近一年使用:0次
2020-02-20更新
|
401次组卷
|
7卷引用:江西省赣州市兴国县2021-2022学年高二上学期联考数学(理)试题
名校
解题方法
7 . 随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加,下表是某购物网站2018年1-8月促销费用(万元)和产品销量(万件)的具体数据:
(1)根据数据绘制的散点图能够看出可用线性回归模型 与
与 的关系,请用相关系数
的关系,请用相关系数 加以说明(系数精确到0.001);
加以说明(系数精确到0.001);
(2)建立 关于
关于 的线性回归方程
的线性回归方程 (系数精确到0.001);如果该公司计划在9月份实现产品销量超6万件,预测至少需要投入费用多少万元(结果精确到0.01).
(系数精确到0.001);如果该公司计划在9月份实现产品销量超6万件,预测至少需要投入费用多少万元(结果精确到0.01).
参考数据: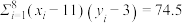 ,
,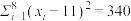 ,
,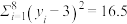 ,
,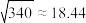 ,
, ,其中
,其中 ,
, 分别为第
分别为第 个月的促销费用和产品销量,
个月的促销费用和产品销量,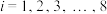 .
.
参考公式:(1)样本 相关系数
相关系数 ;
;
(2)对于一组数据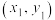 ,
,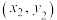 ,…,
,…,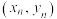 ,其回归方程
,其回归方程 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为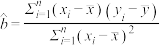 ,
, .
.
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
促销费用 | 2 | 3 | 6 | 10 | 13 | 21 | 15 | 18 |
产品销量 | 1 | 1 | 2 | 3 | 3.5 | 5 | 4 | 4.5 |
(1)根据数据绘制的散点图能够看出可用线性回归模型
 与
与 的关系,请用相关系数
的关系,请用相关系数 加以说明(系数精确到0.001);
加以说明(系数精确到0.001);(2)建立
 关于
关于 的线性回归方程
的线性回归方程 (系数精确到0.001);如果该公司计划在9月份实现产品销量超6万件,预测至少需要投入费用多少万元(结果精确到0.01).
(系数精确到0.001);如果该公司计划在9月份实现产品销量超6万件,预测至少需要投入费用多少万元(结果精确到0.01).参考数据:
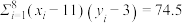 ,
,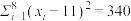 ,
,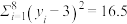 ,
,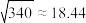 ,
, ,其中
,其中 ,
, 分别为第
分别为第 个月的促销费用和产品销量,
个月的促销费用和产品销量,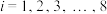 .
.参考公式:(1)样本
 相关系数
相关系数 ;
;(2)对于一组数据
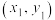 ,
,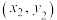 ,…,
,…,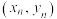 ,其回归方程
,其回归方程 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为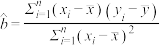 ,
, .
.
您最近一年使用:0次
2020-05-22更新
|
212次组卷
|
2卷引用:江西省宜春市上高县第二中学2019-2020学年高二下学期第一次月考(5月)数学(文)试题
名校
8 . 新能源汽车的春天来了!2018年3月5日上午,李克强总理做政府工作报告时表示,将新能源汽车车辆购置税优惠政策再延长三年,自2018年1月1日至2020年12月31日,对购置的新能源汽车免征车辆购置税.某人计划于2018年5月购买一辆某品牌新能源汽车,他从当地该品牌销售网站了解了近五个月的实际销量如下表:
(1)经分析,可用线性回归模型拟合当地该品牌新能源汽车实际销量 (万辆)与月份编号
(万辆)与月份编号 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求 关于
关于 的线性回归方程
的线性回归方程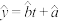 ,并预测2018年5月份当地该品牌新能源汽车的销量;
,并预测2018年5月份当地该品牌新能源汽车的销量;
(2)2018年6月12日,中央财政和地方财政将根据新能源汽车的最大续航里程(新能源汽车的最大续航里程是指理论上新能源汽车所装的燃料或电池所能够提供给车跑的最远里程)对购车补贴进行新一轮调整.已知某地拟购买新能源汽车的消费群体十分庞大,某调研机构对其中的200名消费者的购车补贴金额的心理预期值进行了一个抽样调查,得到如下一份频数表:
(i)求这200位拟购买新能源汽车的消费者对补贴金额的心理预期值 的方差
的方差 及中位数的估计值(同一区间的预期值可用该区间的中点值代替,估计值精确到0.1);
及中位数的估计值(同一区间的预期值可用该区间的中点值代替,估计值精确到0.1);
(ii)将频率视为概率,现用随机抽样方法从该地区拟购买新能源汽车的所有消费者中随机抽取3人,记被抽取的3人中对补贴金额的心理预期值不低于3万元的人数为 ,求
,求 的分布列及数学期望
的分布列及数学期望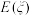 .
.
附:①回归直线的斜率和截距的最小二乘估计公式分别为: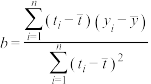 ,
,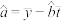 ;②
;②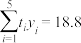 .
.
月份 | 2017.12 | 2018.01 | 2018.02 | 2018.03 | 2018.04 |
月份编号 | 1 | 2 | 3 | 4 | 5 |
销量(万量) | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
 (万辆)与月份编号
(万辆)与月份编号 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求 关于
关于 的线性回归方程
的线性回归方程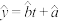 ,并预测2018年5月份当地该品牌新能源汽车的销量;
,并预测2018年5月份当地该品牌新能源汽车的销量;(2)2018年6月12日,中央财政和地方财政将根据新能源汽车的最大续航里程(新能源汽车的最大续航里程是指理论上新能源汽车所装的燃料或电池所能够提供给车跑的最远里程)对购车补贴进行新一轮调整.已知某地拟购买新能源汽车的消费群体十分庞大,某调研机构对其中的200名消费者的购车补贴金额的心理预期值进行了一个抽样调查,得到如下一份频数表:
补贴金额预期值区间(万元) |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
 的方差
的方差 及中位数的估计值(同一区间的预期值可用该区间的中点值代替,估计值精确到0.1);
及中位数的估计值(同一区间的预期值可用该区间的中点值代替,估计值精确到0.1);(ii)将频率视为概率,现用随机抽样方法从该地区拟购买新能源汽车的所有消费者中随机抽取3人,记被抽取的3人中对补贴金额的心理预期值不低于3万元的人数为
 ,求
,求 的分布列及数学期望
的分布列及数学期望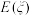 .
.附:①回归直线的斜率和截距的最小二乘估计公式分别为:
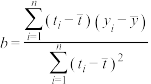 ,
,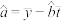 ;②
;②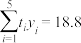 .
.
您最近一年使用:0次
2019-11-14更新
|
636次组卷
|
3卷引用:江西省九江市实验中学2021-2022学年高二下学期5月阶段性水平测试数学(理)试题
9 . 某部门经统计,客户对不同款型理财产品的最满意程度百分比和对应的理财总销售量(万元)如下表(最满意度百分比超高时总销售量最高):
设 表示理财产品最满意度的百分比,
表示理财产品最满意度的百分比, 为该理财产品的总销售量(万元).这些数据的散点图如图所示.
为该理财产品的总销售量(万元).这些数据的散点图如图所示.

(1)在 份
份 款型理财产品的顾客满意度调查资料中任取
款型理财产品的顾客满意度调查资料中任取 份;只有一份最满意的,求含有最满意客户资料事件的概率.
份;只有一份最满意的,求含有最满意客户资料事件的概率.
(2)我们约定:相关系数的绝对值在 以下是无线性相关,在
以下是无线性相关,在 以上(含
以上(含 )至
)至 是一般线性相关,在
是一般线性相关,在 以上(含
以上(含 )是较强线性相关,若没有达到较强线性相关则采取“末位”剔除制度(即总销售量最少的那一款产品退出理财销售);试求在剔除“末位”款型后的线性回归方程(系数精确到
)是较强线性相关,若没有达到较强线性相关则采取“末位”剔除制度(即总销售量最少的那一款产品退出理财销售);试求在剔除“末位”款型后的线性回归方程(系数精确到 ).
).
数据参考计算值:
附:回归直线方程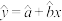 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为:
线性相关系数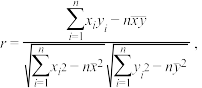
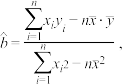
 .
.
产品款型 | A | B | C | D | E | F | G | H | I | J |
最满意度% | 20 | 34 | 25 | 19 | 26 | 20 | 19 | 24 | 19 | 13 |
总销量(万元) | 80 | 89 | 89 | 78 | 75 | 71 | 65 | 62 | 60 | 52 |
 表示理财产品最满意度的百分比,
表示理财产品最满意度的百分比, 为该理财产品的总销售量(万元).这些数据的散点图如图所示.
为该理财产品的总销售量(万元).这些数据的散点图如图所示.
(1)在
 份
份 款型理财产品的顾客满意度调查资料中任取
款型理财产品的顾客满意度调查资料中任取 份;只有一份最满意的,求含有最满意客户资料事件的概率.
份;只有一份最满意的,求含有最满意客户资料事件的概率.(2)我们约定:相关系数的绝对值在
 以下是无线性相关,在
以下是无线性相关,在 以上(含
以上(含 )至
)至 是一般线性相关,在
是一般线性相关,在 以上(含
以上(含 )是较强线性相关,若没有达到较强线性相关则采取“末位”剔除制度(即总销售量最少的那一款产品退出理财销售);试求在剔除“末位”款型后的线性回归方程(系数精确到
)是较强线性相关,若没有达到较强线性相关则采取“末位”剔除制度(即总销售量最少的那一款产品退出理财销售);试求在剔除“末位”款型后的线性回归方程(系数精确到 ).
).数据参考计算值:
| 项目 |  | 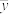 | 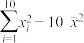 | 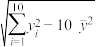 |  |  |
| 值 | 21.9 | 72.1 | 288.9 | 37.16 | 452.1 | 17.00 |
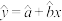 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为:线性相关系数
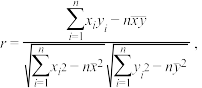
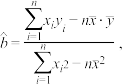
 .
.
您最近一年使用:0次
名校
解题方法
10 . 某5G科技公司对某款5G产品在2020年1月至6月的月销售量及月销售单价进行了调查,月销售单价x和月销售量y之间的一组数据如表所示:
(1)由散点图可知变量y与x具有线性相关关系,根据1月至6月的数据,求出y关于x的回归直线方程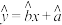 ;
;
(2)预计在今后的销售中,月销售量与月销售单价仍然服从(1)中的关系,若该种产品的成本是350元/件,则该产品的月销售单价应定为多少元才能获得最大月利润?(注:利润=销售收入-成本)
参考公式和部分数据: ,
, .
.
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 月销售单价x(百元) | 9 | 8.8 | 8.6 | 8.4 | 8.2 | 8 |
| 月销售量y(万件) | 68 | 75 | 80 | 83 | 84 | 90 |
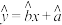 ;
;(2)预计在今后的销售中,月销售量与月销售单价仍然服从(1)中的关系,若该种产品的成本是350元/件,则该产品的月销售单价应定为多少元才能获得最大月利润?(注:利润=销售收入-成本)
参考公式和部分数据:
 ,
, .
.
您最近一年使用:0次
2021-07-05更新
|
146次组卷
|
2卷引用:江西省新余市2020-2021学年高一下学期期末数学(文)试题