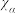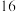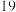解题方法
1 . 为了了解高中学生课后自主学习数学时间( 分钟/每天)和他们的数学成绩(y分)的关系,某实验小组做了调查,得到一些数据(表一).
分钟/每天)和他们的数学成绩(y分)的关系,某实验小组做了调查,得到一些数据(表一).
(1)求数学成绩 与学习时间
与学习时间 的相关系数(精确到0.001);
的相关系数(精确到0.001);
(2)请用相关系数说明该组数据中 与
与 之间的关系可用线性回归模型进行拟合,并求出
之间的关系可用线性回归模型进行拟合,并求出 关于
关于 的回归直线方程,并由此预测每天课后自主学习数学时间为100分钟时的数学成绩(参考数据:
的回归直线方程,并由此预测每天课后自主学习数学时间为100分钟时的数学成绩(参考数据: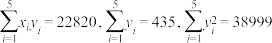 ,
,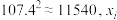 的方差为200
的方差为200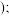
(3)基于上述调查,某校提倡学生周末在校自主学习.经过一学期的实施后,抽样调查了220位学生.按照是否参与周末在校自主学习以及成绩是否有进步统计,得到 列联表(表二).依据表中数据及小概率值
列联表(表二).依据表中数据及小概率值 的独立性检验,分析“周末在校自主学习与成绩进步”是否有关.
的独立性检验,分析“周末在校自主学习与成绩进步”是否有关.
附: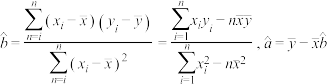 ,
,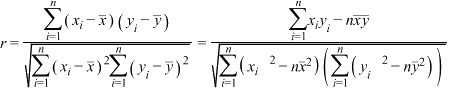
 .
.
 分钟/每天)和他们的数学成绩(y分)的关系,某实验小组做了调查,得到一些数据(表一).
分钟/每天)和他们的数学成绩(y分)的关系,某实验小组做了调查,得到一些数据(表一).| 编号 | 1 | 2 | 3 | 4 | 5 |
学习时间 | 30 | 40 | 50 | 60 | 70 |
数学成绩 | 65 | 78 | 85 | 99 | 108 |
(1)求数学成绩
 与学习时间
与学习时间 的相关系数(精确到0.001);
的相关系数(精确到0.001);(2)请用相关系数说明该组数据中
 与
与 之间的关系可用线性回归模型进行拟合,并求出
之间的关系可用线性回归模型进行拟合,并求出 关于
关于 的回归直线方程,并由此预测每天课后自主学习数学时间为100分钟时的数学成绩(参考数据:
的回归直线方程,并由此预测每天课后自主学习数学时间为100分钟时的数学成绩(参考数据: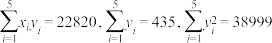 ,
,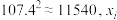 的方差为200
的方差为200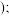
(3)基于上述调查,某校提倡学生周末在校自主学习.经过一学期的实施后,抽样调查了220位学生.按照是否参与周末在校自主学习以及成绩是否有进步统计,得到
 列联表(表二).依据表中数据及小概率值
列联表(表二).依据表中数据及小概率值 的独立性检验,分析“周末在校自主学习与成绩进步”是否有关.
的独立性检验,分析“周末在校自主学习与成绩进步”是否有关.| 没有进步 | 有进步 | 合计 | |
| 参与周末在校自主学习 | 35 | 130 | 165 |
| 未参与周末不在校自主学习 | 25 | 30 | 55 |
| 合计 | 60 | 160 | 220 |
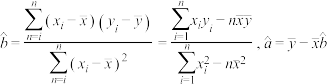 ,
,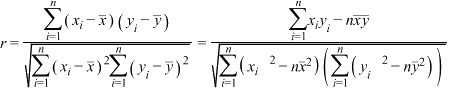
 .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
名校
解题方法
2 . 红旗淀粉厂2024年之前只生产食品淀粉,下表为年投入资金 (万元)与年收益
(万元)与年收益 (万元)的8组数据:
(万元)的8组数据:
(1)用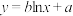 模拟生产食品淀粉年收益
模拟生产食品淀粉年收益 与年投入资金
与年投入资金 的关系,求出回归方程;
的关系,求出回归方程;
(2)为响应国家“加快调整产业结构”的号召,该企业又自主研发出一种药用淀粉,预计其收益为投入的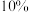 .2024年该企业计划投入200万元用于生产两种淀粉,求年收益的最大值.(精确到0.1万元)
.2024年该企业计划投入200万元用于生产两种淀粉,求年收益的最大值.(精确到0.1万元)
附:①回归直线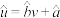 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: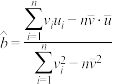 ,
,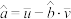
②
③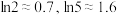
 (万元)与年收益
(万元)与年收益 (万元)的8组数据:
(万元)的8组数据: | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
 | 12.8 | 16.5 | 19 | 20.9 | 21.5 | 21.9 | 23 | 25.4 |
(1)用
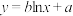 模拟生产食品淀粉年收益
模拟生产食品淀粉年收益 与年投入资金
与年投入资金 的关系,求出回归方程;
的关系,求出回归方程;(2)为响应国家“加快调整产业结构”的号召,该企业又自主研发出一种药用淀粉,预计其收益为投入的
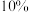 .2024年该企业计划投入200万元用于生产两种淀粉,求年收益的最大值.(精确到0.1万元)
.2024年该企业计划投入200万元用于生产两种淀粉,求年收益的最大值.(精确到0.1万元)附:①回归直线
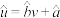 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: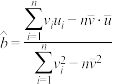 ,
,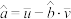
②
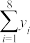 | 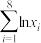 | 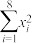 | 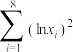 | 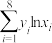 |
| 161 | 29 | 20400 | 109 | 603 |
您最近一年使用:0次
2024-03-22更新
|
1489次组卷
|
2卷引用:浙江省温州市2024届高三第二次适应性考试数学试题
解题方法
3 . 中国共产党第二十次全国代表大会报告指出:坚持精准治污、科学治污、依法治污,持续深入打好蓝天、碧水、净土保卫战,加强污染物协同控制,基本消除重污染天气、每年的《中国生态环境状态公报》都会公布全国339个地级及以上城市空气质量检测报告,以下是2017-2021五年339个城市空气质量平均优良天数占比统计表.
并计算得: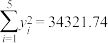 ,
, .
.
(1)求2017年—2021年年份代码与339个城市空气质量平均优良天数的百分比的样本相关系数(精确到0.01);
(2)请用相关系数说明该组数据中y与x之间的关系可用线性回归模型进行拟合,并求出y关于x的回归直线方程(精确到0.01)和预测2022年( )的空气质量优良天数的百分比;
)的空气质量优良天数的百分比;
(3)试判断用所求回归方程是否可预测2026年( )的空气质量优良天数的百分比,并说明理由.
)的空气质量优良天数的百分比,并说明理由.
(回归直线的斜率和截距的最小二乘法估计公式分别为: ,
, )
)
附:相关系数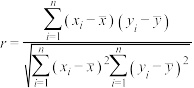 ,
, ,
, .
.
| 年份 | 2017年 | 2018年 | 2019年 | 2020年 | 2021年 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
百分比 | 78 | 79.3 | 82 | 87 | 87.5 |
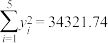 ,
, .
.(1)求2017年—2021年年份代码与339个城市空气质量平均优良天数的百分比的样本相关系数(精确到0.01);
(2)请用相关系数说明该组数据中y与x之间的关系可用线性回归模型进行拟合,并求出y关于x的回归直线方程(精确到0.01)和预测2022年(
 )的空气质量优良天数的百分比;
)的空气质量优良天数的百分比;(3)试判断用所求回归方程是否可预测2026年(
 )的空气质量优良天数的百分比,并说明理由.
)的空气质量优良天数的百分比,并说明理由.(回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
, )
)附:相关系数
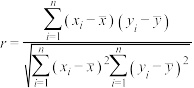 ,
, ,
, .
.
您最近一年使用:0次
解题方法
4 . 流行性感冒(简称流感)是流感病毒引起的急性呼吸道感染,是一种传染性强、传播速度快的疾病.其主要通过空气中的飞沫、人与人之间的接触或与被污染物品的接触传播.流感每年在世界各地均有传播,在我国北方通常呈冬春季流行,南方有冬春季和夏季两个流行高峰.某幼儿园将去年春季该园患流感小朋友按照年龄与人数统计,得到如下数据:
(1)求 关于
关于 的经验回归方程;
的经验回归方程;
(2)计算变量 、
、 的样本相关系数
的样本相关系数 (计算结果精确到
(计算结果精确到 ),并判断是否可以认为该幼儿园去年春季患流感人数与年龄负相关程度很强.(若
),并判断是否可以认为该幼儿园去年春季患流感人数与年龄负相关程度很强.(若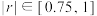 ,则
,则 、
、 相关程度很强;若
相关程度很强;若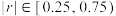 ,则
,则 、
、 相关程度一般:若
相关程度一般:若 ,则
,则 、
、 相关程度较弱.)参考数据:
相关程度较弱.)参考数据: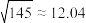 .
.
年龄 |
|
|
|
|
|
患病人数 |
|
|
|
|
|
 关于
关于 的经验回归方程;
的经验回归方程;(2)计算变量
 、
、 的样本相关系数
的样本相关系数 (计算结果精确到
(计算结果精确到 ),并判断是否可以认为该幼儿园去年春季患流感人数与年龄负相关程度很强.(若
),并判断是否可以认为该幼儿园去年春季患流感人数与年龄负相关程度很强.(若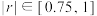 ,则
,则 、
、 相关程度很强;若
相关程度很强;若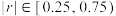 ,则
,则 、
、 相关程度一般:若
相关程度一般:若 ,则
,则 、
、 相关程度较弱.)参考数据:
相关程度较弱.)参考数据: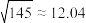 .
.
您最近一年使用:0次