1 . 甲、乙、丙等 人排成一列,下列说法正确的有( )
人排成一列,下列说法正确的有( )
 人排成一列,下列说法正确的有( )
人排成一列,下列说法正确的有( )A.若甲和乙相邻,共有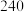 种排法 种排法 | B.若甲不排第一个共有 种排法 种排法 |
C.若甲与丙不相邻,共有 种排法 种排法 | D.若甲在乙的前面,共有 种排法 种排法 |
您最近一年使用:0次
2024-02-13更新
|
1256次组卷
|
8卷引用:第7章 计数原理单元综合能力测试卷(新题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)第7章 计数原理单元综合能力测试卷(新题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)江苏省常州市2023-2024学年高二上学期期末学业水平监测数学试卷(已下线)第六章 计数原理章末综合达标卷-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第三册)江苏省南通市海门中学2023-2024学年高二下学期3月学情调研数学试题(已下线)江苏省连云港市七校2023-2024学年高二下学期期中考试数学试题变式题6-10(已下线)6.2.3组合+6.2.4组合数 第三练 能力提升拔高(已下线)专题2.5排列组合综合(强化训练)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)(已下线)专题02 计数原理-3
2023高三·全国·专题练习
2 . 6男4女站成一排,求满足下列条件的排法各有多少种?(用式子表达)
(1)男甲必排在首位;
(2)男甲、男乙必排在正中间;
(3)男甲不在首位,男乙不在末位;
(4)男甲、男乙必排在一起;
(5)4名女生排在一起;
(6)任何两个女生都不得相邻;
(7)男生甲、乙、丙顺序一定.
(1)男甲必排在首位;
(2)男甲、男乙必排在正中间;
(3)男甲不在首位,男乙不在末位;
(4)男甲、男乙必排在一起;
(5)4名女生排在一起;
(6)任何两个女生都不得相邻;
(7)男生甲、乙、丙顺序一定.
您最近一年使用:0次
3 . 用0,1,2,3,4这5个数字,可以组成多少个满足下列条件的没有重复数字五位数?
(1)偶数:
(2)左起第二、四位是奇数的偶数;
(3)比21034大的偶数.
(1)偶数:
(2)左起第二、四位是奇数的偶数;
(3)比21034大的偶数.
您最近一年使用:0次
2022-09-15更新
|
1683次组卷
|
9卷引用:第7章 计数原理 单元综合检测(练习)
(已下线)第7章 计数原理 单元综合检测(练习)上海市奉贤中学2021-2022学年高二上学期10月月考数学试题(已下线)专题3排列数与组合数混合运算 (提升版)(已下线)专题20 计数原理(练习)-1(已下线)专题20 计数原理(练习)-2(已下线)第01讲 分类加法计数原理与分步乘法计数原理(已下线)6.2.1排列+6.2.2排列数 (精讲)(2)(已下线)拓展一:排列组合18种常考考法归类 -【帮课堂】2022-2023学年高二数学同步精品讲义(人教A版2019选择性必修第三册)(已下线)2023-2024学年高二下学期期中复习解答题压轴题十七大题型专练(2)
名校
解题方法
4 .  名同学
名同学 简记为
简记为 、
、 、
、 、
、 、
、 、
、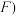 到甲、乙、丙三个场馆做志愿者
到甲、乙、丙三个场馆做志愿者
(1)一天上午有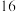 个相同的口罩全部发给这
个相同的口罩全部发给这 名同学,每名同学至少发两个口罩,则不同的发放方法种数?
名同学,每名同学至少发两个口罩,则不同的发放方法种数?
(2)每名同学只去一个场馆,甲场馆安排 名,乙场馆安排
名,乙场馆安排 名,丙场馆安排
名,丙场馆安排 名,则不同的安排方法种数?
名,则不同的安排方法种数?
(3)每名同学只去一个场馆,每个场馆至少要去一名,且 、
、 两人约定去同一个场馆,
两人约定去同一个场馆, 、
、 不想去一个场馆,则满足同学要求的不同的安排方法种数?
不想去一个场馆,则满足同学要求的不同的安排方法种数?
 名同学
名同学 简记为
简记为 、
、 、
、 、
、 、
、 、
、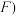 到甲、乙、丙三个场馆做志愿者
到甲、乙、丙三个场馆做志愿者
(1)一天上午有
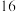 个相同的口罩全部发给这
个相同的口罩全部发给这 名同学,每名同学至少发两个口罩,则不同的发放方法种数?
名同学,每名同学至少发两个口罩,则不同的发放方法种数?(2)每名同学只去一个场馆,甲场馆安排
 名,乙场馆安排
名,乙场馆安排 名,丙场馆安排
名,丙场馆安排 名,则不同的安排方法种数?
名,则不同的安排方法种数?(3)每名同学只去一个场馆,每个场馆至少要去一名,且
 、
、 两人约定去同一个场馆,
两人约定去同一个场馆, 、
、 不想去一个场馆,则满足同学要求的不同的安排方法种数?
不想去一个场馆,则满足同学要求的不同的安排方法种数?
您最近一年使用:0次
2022-04-18更新
|
1535次组卷
|
5卷引用:第7章:计数原理 章末检测试卷
(已下线)第7章:计数原理 章末检测试卷山东省菏泽市菏泽第一中学2021-2022学年高二下学期4月月考数学试题(已下线)6.2.3组合+6.2.4组合数(精练)山东省菏泽市鄄城县鄄城县第一中学2022-2023学年高二下学期5月月考数学试题(已下线)第06讲 排列与组合-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)
名校
解题方法
5 . 将编号为1、2、3、4、5的5个小球全部放入 三个盒子内,若每个盒子不空,且放在同一个盒子内的小球编号不相连,则不同的方法总数有( )
三个盒子内,若每个盒子不空,且放在同一个盒子内的小球编号不相连,则不同的方法总数有( )
 三个盒子内,若每个盒子不空,且放在同一个盒子内的小球编号不相连,则不同的方法总数有( )
三个盒子内,若每个盒子不空,且放在同一个盒子内的小球编号不相连,则不同的方法总数有( )A. | B.36 | C.48 | D.60 |
您最近一年使用:0次
2021-12-19更新
|
1244次组卷
|
13卷引用:第7章 计数原理 单元综合检测(练习)
(已下线)第7章 计数原理 单元综合检测(练习)江苏省南通市如皋中学2020-2021学年高二下学期5月月考数学试题浙江省宁波市北仑中学2020-2021学年高二(1班)上学期期中数学试题(已下线)专题11.2 排列与组合(精讲)-2021年新高考数学一轮复习学与练(已下线)专题11.2 排列与组合(讲)-2021年新高考数学一轮复习讲练测(已下线)6.2.3 排列组合的综合运用(精练)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)(已下线)专题12 排列、组合、二项式定理-2021年高考冲刺之二轮专题精讲精析北京市首都师范大学附属中学2020-2021学年高二上学期期末考试数学试题(已下线)专题11.2 排列与组合 2022年高考数学一轮复习讲练测(新教材新高考)(讲)(已下线)专题46 排列与组合-2022年(新高考)数学高频考点+重点题型(已下线)第10讲 排列与组合-【寒假自学课】2022年高二数学寒假精品课(苏教版2019选择性必修第二册)(已下线)6.2.3-6.2.4 组合 组合数(练习)安徽省2024届新高考数学模拟预测卷(八)
名校
解题方法
6 . 高二全体师生今秋开学前在新校区体验周活动中有优异的表现,学校拟对高二年级进行表彰;
(1)若要表彰3个优秀班级,规定从6个文科班中选一个,14个理科班中选两个班级,有多少种不同的选法?
(2)年级组拟在选出的三个班级中再选5名学生,每班至少1名,最多2名,则不同的分配方案有多少种?
(3)选中的这5名学生和三位年级负责人徐主任,陈主任,付主任排成一排合影留念,规定这3位老师不排两端,且老师顺序固定不变,那么不同的站法有多少种?
(1)若要表彰3个优秀班级,规定从6个文科班中选一个,14个理科班中选两个班级,有多少种不同的选法?
(2)年级组拟在选出的三个班级中再选5名学生,每班至少1名,最多2名,则不同的分配方案有多少种?
(3)选中的这5名学生和三位年级负责人徐主任,陈主任,付主任排成一排合影留念,规定这3位老师不排两端,且老师顺序固定不变,那么不同的站法有多少种?
您最近一年使用:0次



