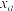23-24高三下·浙江·开学考试
名校
解题方法
1 . 甲、乙、丙三位同学进行乒乓球比赛,约定赛制如下:每场比赛胜者积2分,负者积0分;比赛前根据相关规则决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空;积分首先累计到4分者获得比赛胜利,比赛结束.已知甲与乙比赛时,甲获胜的概率为 ,甲与丙比赛时,甲获胜的概率为
,甲与丙比赛时,甲获胜的概率为 ,乙与丙比赛时,乙获胜的概率为
,乙与丙比赛时,乙获胜的概率为 .
.
(1)若 ,求比赛结束时,三人总积分
,求比赛结束时,三人总积分 的分布列与期望;
的分布列与期望;
(2)若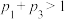 ,假设乙获得了指定首次比赛选手的权利,为获得比赛的胜利,试分析乙的最优指定策略.
,假设乙获得了指定首次比赛选手的权利,为获得比赛的胜利,试分析乙的最优指定策略.
 ,甲与丙比赛时,甲获胜的概率为
,甲与丙比赛时,甲获胜的概率为 ,乙与丙比赛时,乙获胜的概率为
,乙与丙比赛时,乙获胜的概率为 .
.(1)若
 ,求比赛结束时,三人总积分
,求比赛结束时,三人总积分 的分布列与期望;
的分布列与期望;(2)若
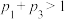 ,假设乙获得了指定首次比赛选手的权利,为获得比赛的胜利,试分析乙的最优指定策略.
,假设乙获得了指定首次比赛选手的权利,为获得比赛的胜利,试分析乙的最优指定策略.
您最近半年使用:0次
2024-02-27更新
|
1686次组卷
|
4卷引用:专题8-2分布列综合归类-2
23-24高二上·浙江杭州·期中
解题方法
2 . 根据历史资料显示,某种慢性疾病患者的自然痊愈率为5%.为试验一种新药,在有关部门批准后,医院将此药给10位病人服用,试验方案为:若这10人中至少有2人痊愈,则认为该药有效,提高了治愈率;否则,则认为该药无效.
(1)如果在该次试验中有5人痊愈,院方欲从参加该次试验的10人中随机选2人了解服药期间的感受,记抽到痊愈的人的个数为X,求X的概率分布.
(2)在第(1)题的条件下求随机变量X的期望与方差.
(3)如果新药有效,将治愈率提高到了50%,求通过试验却认定新药无效的概率P并根据P的值解释该试验方案的合理性.(参考结论:通常认为发生概率小于5%的事件可视为小概率事件).
(1)如果在该次试验中有5人痊愈,院方欲从参加该次试验的10人中随机选2人了解服药期间的感受,记抽到痊愈的人的个数为X,求X的概率分布.
(2)在第(1)题的条件下求随机变量X的期望与方差.
(3)如果新药有效,将治愈率提高到了50%,求通过试验却认定新药无效的概率P并根据P的值解释该试验方案的合理性.(参考结论:通常认为发生概率小于5%的事件可视为小概率事件).
您最近半年使用:0次
23-24高二上·湖北黄冈·阶段练习
名校
解题方法
3 . 第19届亚运会将于2023年9月23日至10月8日举办,本届亚运会共设40个竞赛大项.其中首次增设了电子竞技项目.与传统的淘汰赛不同,近年来一个新型的赛制“双败赛制”赢得了许多赛事的青睐.传统的淘汰赛失败一场就丧失了冠军争夺的权利,而在双败赛制下,每人或者每个队伍只有失败了两场才会淘汰出局,因此更有容错率.假设最终进入到半决赛有四支队伍,淘汰赛制下会将他们四支队伍两两分组进行比赛,胜者进入到总决赛,总决赛的胜者即为最终的冠军.双败赛制下,两两分组,胜者进入到胜者组,败者进入到败者组,胜者组两个队伍对决的胜者将进入到总决赛,败者进入到败者组.之前进入到败者组的两个队伍对决的败者将直接淘汰,胜者将跟胜者组的败者对决,其中的胜者进入总决赛,最后总决赛的胜者即为冠军,双败赛制下会发现一个有意思的事情,在胜者组中的胜者只要输一场比赛即总决赛就无法拿到冠军,但是其它的队伍却有一次失败的机会,近年来从败者组杀上来拿到冠军的不在少数,因此很多人戏谑这个赛制对强者不公平,是否真的如此呢?

这里我们简单研究一下两个赛制,假设四支队伍分别为A、B、C、D,其中A对阵其他三个队伍获胜概率均为p,另外三支队伍彼此之间对阵时获胜概率均为 .最初分组时AB同组,CD同组.
.最初分组时AB同组,CD同组.
(1)若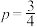 ,在淘汰赛赛制下,A、C获得冠军的概率分别为多少?
,在淘汰赛赛制下,A、C获得冠军的概率分别为多少?
(2)分别计算两种赛制下A获得冠军的概率(用 表示),并据此简单分析一下双败赛制下对队伍的影响,是否如很多人质疑的“对强者不公平”?
表示),并据此简单分析一下双败赛制下对队伍的影响,是否如很多人质疑的“对强者不公平”?

这里我们简单研究一下两个赛制,假设四支队伍分别为A、B、C、D,其中A对阵其他三个队伍获胜概率均为p,另外三支队伍彼此之间对阵时获胜概率均为
 .最初分组时AB同组,CD同组.
.最初分组时AB同组,CD同组.(1)若
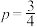 ,在淘汰赛赛制下,A、C获得冠军的概率分别为多少?
,在淘汰赛赛制下,A、C获得冠军的概率分别为多少?(2)分别计算两种赛制下A获得冠军的概率(用
 表示),并据此简单分析一下双败赛制下对队伍的影响,是否如很多人质疑的“对强者不公平”?
表示),并据此简单分析一下双败赛制下对队伍的影响,是否如很多人质疑的“对强者不公平”?
您最近半年使用:0次
2023-10-10更新
|
927次组卷
|
6卷引用:专题03 条件概率与全概率公式(2)
(已下线)专题03 条件概率与全概率公式(2)(已下线)专题10.6 概率全章八大压轴题型归纳(拔尖篇-举一反三系列(人教A版2019必修第二册)湖北省黄冈市黄州中学(黄冈外校)2023-2024学年高二实验朝阳班上学期9月阶段性测试数学试题安徽省合肥市长丰县第一中学2023-2024学年高二上学期第一次月考数学考试试题(已下线)12.4 随机事件的独立性(四大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020必修第三册)单元测试B卷——第十章?概率
22-23高一·全国·随堂练习
4 . 根据统计,某篮球运动员在5000次投篮中,命中的次数为2348次.
(1)求这名运动员的投篮命中率;
(2)若这名运动员要想投篮命中10000次,则大概需要投篮多少次?(结果精确到100)
(3)根据提供的信息,判断“该篮球运动员投篮3次,至少能命中1次”这一说法是否正确.
(1)求这名运动员的投篮命中率;
(2)若这名运动员要想投篮命中10000次,则大概需要投篮多少次?(结果精确到100)
(3)根据提供的信息,判断“该篮球运动员投篮3次,至少能命中1次”这一说法是否正确.
您最近半年使用:0次
2023-10-08更新
|
118次组卷
|
5卷引用:专题10.5 概率全章九大基础题型归纳(基础篇)-举一反三系列(人教A版2019必修第二册)
(已下线)专题10.5 概率全章九大基础题型归纳(基础篇)-举一反三系列(人教A版2019必修第二册)北师大版(2019)必修第一册课本习题 习题7-310.3.1频率的稳定性练习(已下线)习题 7-3(已下线)10.3.1&10.3.2?频率的稳定性、随机模拟——随堂检测
22-23高一·全国·随堂练习
5 . 甲、乙两人约定玩一种游戏,把一枚均匀的骰子连续抛掷3次,游戏规则有下述3种,这3种规则是否公平?对谁更有利?为什么?
(1)若三次掷出的点数之和为奇数,则甲获胜;若三次掷出的点数之和为偶数,则乙获胜.
(2)若三次掷出的点数为一奇两偶或两奇一偶,则甲获胜;若三次掷出的点数均为奇数或均为偶数,则乙获胜.
(3)若三次掷出的点数之和为3,4,5,6,7,14,15,16,17,18其中之一,则甲获胜;否则乙获胜.
(1)若三次掷出的点数之和为奇数,则甲获胜;若三次掷出的点数之和为偶数,则乙获胜.
(2)若三次掷出的点数为一奇两偶或两奇一偶,则甲获胜;若三次掷出的点数均为奇数或均为偶数,则乙获胜.
(3)若三次掷出的点数之和为3,4,5,6,7,14,15,16,17,18其中之一,则甲获胜;否则乙获胜.
您最近半年使用:0次
22-23高一·全国·随堂练习
6 . 某学校校庆,给每班发了5张庆典门票.班主任王老师准备采用抽签方式来决定哪5位同学参加,为此制作了50张卡片,其中5张写有“庆典”字样.50位同学轮流抽签,抽中写有“庆典”字样的同学参加学校庆典.小明提出:“抽签有先后,第一名同学抽中的概率是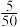 .如果第一名同学抽到,第二名同学抽到的概率只有
.如果第一名同学抽到,第二名同学抽到的概率只有 ,如果第一名同学未抽中,第二名同学抽中的概率为
,如果第一名同学未抽中,第二名同学抽中的概率为 .抽中的机会未必相等.”你认为王老师的抽签方法公平吗?小明的话又如何解释?
.抽中的机会未必相等.”你认为王老师的抽签方法公平吗?小明的话又如何解释?
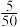 .如果第一名同学抽到,第二名同学抽到的概率只有
.如果第一名同学抽到,第二名同学抽到的概率只有 ,如果第一名同学未抽中,第二名同学抽中的概率为
,如果第一名同学未抽中,第二名同学抽中的概率为 .抽中的机会未必相等.”你认为王老师的抽签方法公平吗?小明的话又如何解释?
.抽中的机会未必相等.”你认为王老师的抽签方法公平吗?小明的话又如何解释?
您最近半年使用:0次
22-23高一下·福建·期末
名校
7 . 某小区为了调查本小区业主对物业服务满意度的真实情况,对本小区业主进行了调查,调查中问了两个问题1:你的手机尾号是不是奇数?问题2:你是否满意物业的服务?调查者设计了一个随机化装置,其中装有大小、形状和质量完全相同的白球和红球,每个被调查者随机从装置中摸到红球和白球的可能性相同,其中摸到白球的业主回答第一个问题,摸到红球的业主回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不要做,由于问题的答案只有“是”和“否”,而且回答的是哪个问题别人并不知道,因此被调查者可以毫无顾虑地给出符合实际情况的答案.已知某小区80名业主参加了问卷,且有48名业主回答了“是”,由此估计本小区对物业满意服务的百分比大约为( )
| A.10% | B.20% | C.35% | D.70% |
您最近半年使用:0次
22-23高二下·浙江舟山·期末
名校
解题方法
8 . 第19届亚运会将于2023年9月23日在杭州开幕,本届亚运会共设40个竞赛大项,包括31个奥运项目和9个非奥运项目.同时,在保持40个大项目不变的前提下,增设电子竞技、霹雳舞两个竞赛项目.为研究不同性别学生对杭州亚运会项目的了解情况,某学校进行了一次抽样调查,被调查的男女生人数相同,其中“了解”的学生中男生人数是女生的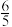 倍.若统计发现在女生中“了解”和“不了解”的人数恰好一样多,应用卡方独立性检验提出零假设为
倍.若统计发现在女生中“了解”和“不了解”的人数恰好一样多,应用卡方独立性检验提出零假设为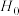 :该校学生对杭州亚运会项目的了解情况与性别无关联,经计算得到
:该校学生对杭州亚运会项目的了解情况与性别无关联,经计算得到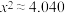 .
.
(1)根据频率稳定于概率的原理,分析性别是否会影响学生对杭州亚运会项目的了解情况;
(2)求被抽样调查的总人数,并依据小概率值 的卡方独立性检验,分析该校学生对杭州亚运会项目的了解情况与性别是否有关联;
的卡方独立性检验,分析该校学生对杭州亚运会项目的了解情况与性别是否有关联;
(3)用样本的频率估计概率,从该校全体学生中随机抽取10人,其中对亚运会项目“了解”的人数记为 ,求随机变量
,求随机变量 的方差.
的方差.
附:
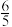 倍.若统计发现在女生中“了解”和“不了解”的人数恰好一样多,应用卡方独立性检验提出零假设为
倍.若统计发现在女生中“了解”和“不了解”的人数恰好一样多,应用卡方独立性检验提出零假设为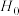 :该校学生对杭州亚运会项目的了解情况与性别无关联,经计算得到
:该校学生对杭州亚运会项目的了解情况与性别无关联,经计算得到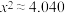 .
.(1)根据频率稳定于概率的原理,分析性别是否会影响学生对杭州亚运会项目的了解情况;
(2)求被抽样调查的总人数,并依据小概率值
 的卡方独立性检验,分析该校学生对杭州亚运会项目的了解情况与性别是否有关联;
的卡方独立性检验,分析该校学生对杭州亚运会项目的了解情况与性别是否有关联;(3)用样本的频率估计概率,从该校全体学生中随机抽取10人,其中对亚运会项目“了解”的人数记为
 ,求随机变量
,求随机变量 的方差.
的方差.附:

a | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近半年使用:0次
2023-07-19更新
|
307次组卷
|
3卷引用:第十章 综合测试A(基础卷)
22-23高一下·新疆喀什·期末
名校
9 . 下列说法正确的是( )
| A.随着试验次数的增大,随机事件发生的频率会逐渐稳定于该随机事件发生的概率 |
B.某种福利彩票的中奖概率为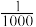 ,买1000张这种彩票一定能中奖 ,买1000张这种彩票一定能中奖 |
C.连续100次掷一枚硬币,结果出现了49次反面,则掷一枚硬币出现反面的概率为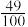 |
| D.某市气象台预报“明天本市降水概率为70%”,指的是:该市气象台专家中,有70%认为明天会降水,30%认为明天不会降水 |
您最近半年使用:0次
2023-07-16更新
|
361次组卷
|
6卷引用:3频率与概率-同步精品课堂(北师大版2019必修第一册)
(已下线)3频率与概率-同步精品课堂(北师大版2019必修第一册)(已下线)15.2 随机事件的概率-【帮课堂】(苏教版2019必修第二册)(已下线)专题10.3 频率与概率-举一反三系列(人教A版2019必修第二册)(已下线)专题10.5 概率全章九大基础题型归纳(基础篇)-举一反三系列(人教A版2019必修第二册)新疆维吾尔自治区喀什地区巴楚县2022-2023学年高一下学期7月期末考试数学试题甘肃省天水市第一中学2023-2024学年高二上学期开学考试数学试题
22-23高一下·重庆·期末
解题方法
10 . 小颖的爸爸只有一张《阿凡达》的电影票,她和哥哥两人都很想去观看.哥哥想了一个办法,他拿了8张扑克牌,将数字为2,3,5,9的四张牌给小颖,将数字为4,6,7,10的四张牌给自己,并按如下游戏规则进行:小颖和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数,则小颖去;如果和为奇数,则哥哥去.
(1)求小颖去看电影的概率;
(2)这个游戏规则公平吗?若公平,请说明理由,若不公平,在小颖和哥哥所拿4张牌不变的情况下,如何修改游戏规则使其对双方公平.
(1)求小颖去看电影的概率;
(2)这个游戏规则公平吗?若公平,请说明理由,若不公平,在小颖和哥哥所拿4张牌不变的情况下,如何修改游戏规则使其对双方公平.
您最近半年使用:0次