名校
解题方法
1 . 在一个袋中装有大小、形状完全相同的3个红球、2个黄球.现从中任取2个球,设随机变量X为取得红球的个数.
(1)求X的分布列;
(2)求X的数学期望 和方差
和方差 .
.
(1)求X的分布列;
(2)求X的数学期望
 和方差
和方差 .
.
您最近一年使用:0次
2023-08-14更新
|
315次组卷
|
8卷引用:陕西省延安市第一中学2019-2020学年高二下学期6月月考数学(理)试题
陕西省延安市第一中学2019-2020学年高二下学期6月月考数学(理)试题(已下线)7.4 二项分布与超几何分布(精练)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)(已下线)第七章 随机变量及其分布 讲核心 02黑龙江省牡丹江市第二高级中学2022-2023学年高二下学期6月月考数学试题(已下线)6.3.2离散型随机变量的方差(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)(已下线)7.3.2 离散型随机变量的方差——课后作业(巩固版)(已下线)第7.3.2讲 离散型随机变量的方差-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第三册)(已下线)第七章 随机变量及其分布 讲核心 02
解题方法
2 . 已知随机变量X的分布列为
若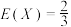 ,
,
(1)求 的值;
的值;
(2)若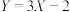 ,求
,求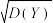 的值.
的值.
X | 0 | 1 | x |
P |
|
| p |
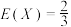 ,
,(1)求
 的值;
的值;(2)若
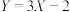 ,求
,求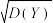 的值.
的值.
您最近一年使用:0次
2023-08-01更新
|
940次组卷
|
21卷引用:高中数学人教A版选修2-3 第二章 随机变量及其分布 2.3.2 离散型随机变量的方差
高中数学人教A版选修2-3 第二章 随机变量及其分布 2.3.2 离散型随机变量的方差西藏自治区拉萨市拉萨那曲第二高级中学2018-2019学年高二下学期期末数学(理)试题辽宁省葫芦岛市实验中学东戴河分校2019-2020学年高二下学期期中考试数学试题(已下线)突破2.3离散型随机变的均值与方差-突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)(已下线)专题14 计数原理、随机变量的数字特征 第一篇 热点、难点突破篇(讲)-2021年高考数学二轮复习讲练测(浙江专用)北师大版(2019) 选修第一册 突围者 第六章 第三节 课时2 离散型随机变量的方差(已下线)专题14 计数原理、随机变量的数字特征(讲)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(浙江专用)》6.3.2离散型随机变量的方差 同步练习6.3.2离散型随机变量的方差 课时作业新疆博湖县奇石中学2022-2023学年高二下学期期末考试数学试题(已下线)专题21 离散型随机变量的均值、方差与标准差(重点突围)-【学霸满分】2022-2023学年高二数学下学期重难点专题提优训练(苏教版2019选择性必修第二册)(已下线)第07讲 离散型随机变量的分布列与数字特征(六大题型)(讲义)(已下线)第10讲 离散型随机变量的均值与方差-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)专题12随机变量及其分布 (十六大题型+过关检测专训)(3)(已下线)专题12随机变量及其分布 (十六大题型+过关检测专训)(1)(已下线)第05讲 7.3.2离散型随机变量的方差-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)专题7.8 随机变量及其分布全章十一大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第八章 概率(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第二册)(已下线)7.3.2 离散型随机变量的方差——课后作业(基础版)(已下线)第7.3.2讲 离散型随机变量的方差-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第三册)新疆兵团第三师图木舒克市鸿德实验学校2023-2024学年高二下学期第二次月考数学试卷
名校
3 . 有甲、乙两家公司都需要招聘求职者,这两家公司的聘用信息如表所示.
(1)若一人去应聘甲公司的C职位,另一人去应聘乙公司的C职位,记这两人被录用的人数和为 ,求
,求 的分布列.
的分布列.
(2)若小方和小芳分别被甲、乙两家公司录用,求小方月薪高于小芳月薪的概率.
(3)根据甲、乙两家公司的聘用信息,如果你是求职者,你会选择哪一家公司?说明理由.
甲公司 | 乙公司 | ||||||||
职位 | A | B | C | D | 职位 | A | B | C | D |
月薪/千元 | 5 | 6 | 7 | 8 | 月薪/千元 | 4 | 6 | 8 | 10 |
获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 | 获得相应职位概率 | 0.4 | 0.3 | 0.2 | 0.1 |
 ,求
,求 的分布列.
的分布列.(2)若小方和小芳分别被甲、乙两家公司录用,求小方月薪高于小芳月薪的概率.
(3)根据甲、乙两家公司的聘用信息,如果你是求职者,你会选择哪一家公司?说明理由.
您最近一年使用:0次
2022-06-09更新
|
982次组卷
|
8卷引用:【校级联考】福建省三明市三地三校2018-2019学年高二下学期期中联考数学(理)试题
【校级联考】福建省三明市三地三校2018-2019学年高二下学期期中联考数学(理)试题北师大版(2019) 选修第一册 必杀技 第六章 素养检测人教A版(2019) 选修第三册 必杀技 第七章检测辽宁省渤海大学附属高级中学2021-2022学年高二4月份阶段性考试数学试题(已下线)第七章 随机变量及其分布 讲核心 01(已下线)第七章 随机变量及其分布 讲核心 02(已下线)7.3.2离散型随机变量的方差(精练)(已下线)第五章 概率统计创新问题 专题一 概率统计决策问题 微点1 概率统计决策问题(一)【基础版】
19-20高二下·江苏苏州·期中
名校
4 . 假定某射手每次射击命中目标的概率为 ,现有
,现有 发子弹,该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用的子弹数为
发子弹,该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用的子弹数为 .
.
(1)试求使用 发子弹击中目标的概率;
发子弹击中目标的概率;
(2)求数学期望 .
.
 ,现有
,现有 发子弹,该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用的子弹数为
发子弹,该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用的子弹数为 .
.(1)试求使用
 发子弹击中目标的概率;
发子弹击中目标的概率;(2)求数学期望
 .
.
您最近一年使用:0次
5 . 产品质量是企业的生命线,为提高产品质量.企业非常重视产品生产线的质量,某企业引进了生产同一种产品的A,B两条生产线,为比较两条生产线的质量,从A,B生产线生产的产品中各自随机抽取了100件产品进行检测,把产品等级结果和频数制成了如图的统计图.
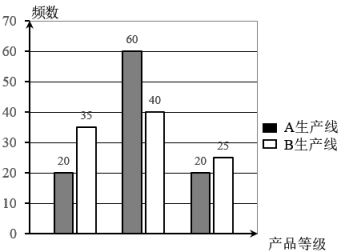
(1)有多大的把握认为一级品与生产线有关?
(2)生产一件一级品可盈利100元,生产一件二级品可盈利50元,生产一件三级品则亏损20元,以频率估计概率.
①分别估计A,B生产线生产一件产品的平均利润;
②你认为哪条生产线的利润较为稳定?并说明理由.
附:①参考公式: ,其中
,其中 .
.
②临界表值:

(1)有多大的把握认为一级品与生产线有关?
(2)生产一件一级品可盈利100元,生产一件二级品可盈利50元,生产一件三级品则亏损20元,以频率估计概率.
①分别估计A,B生产线生产一件产品的平均利润;
②你认为哪条生产线的利润较为稳定?并说明理由.
附:①参考公式:
 ,其中
,其中 .
.②临界表值:
 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
您最近一年使用:0次
2021-01-09更新
|
108次组卷
|
2卷引用:陕西省榆林市第十中学2020-2021学年高三上学期第五次模拟考试理科数学试题
20-21高二上·全国·单元测试
名校
6 . 甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ与η,且ξ,η的分布列为:
(1)求a,b的值;
(2)计算ξ,η的期望与方差,并以此分析甲、乙技术状况.
ξ | 1 | 2 | 3 |
P | a | 0.1 | 0.6 |
η | 1 | 2 | 3 |
P | 0.3 | b | 0.3 |
(2)计算ξ,η的期望与方差,并以此分析甲、乙技术状况.
您最近一年使用:0次
2021-01-07更新
|
657次组卷
|
12卷引用:人教B版2019选择性必修第二册综合测试(能力提升)-2020-2021学年高二数学单元测试定心卷(人教B版2019选择性必修第二册)
(已下线)人教B版2019选择性必修第二册综合测试(能力提升)-2020-2021学年高二数学单元测试定心卷(人教B版2019选择性必修第二册)(已下线)专题32 离散型随机变量的数字特征-2020-2021学年高中数学新教材人教A版选择性必修配套提升训练(已下线)专题7.3离散型随机变量的数字特征(A卷基础篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)(已下线)专题4.4 随机变量的数字特征(A卷基础篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教B版)(已下线)第五课时 课后 7.3.2 离散型随机变量的方差人教A版(2019) 选修第三册 过关斩将 第七章 7.3.2 离散型随机变量的方差2023版 湘教版(2019) 选修第二册 过关斩将 第3章 3.2.4离散型随机变量的方差(已下线)7.3.2 离散型随机变量的方差(1)广西壮族自治区河池市三新学术联盟2022-2023学年高二下学期5月期中数学试题黑龙江省哈尔滨市方正县高楞高级中学校2022-2023学年高二下学期期中数学试题北师大版(2019) 选修第一册 数学奇书 第六章 概率 §3 离散型随机变量的均值与方差 3.2 离散型随机变量的方差安徽省蚌埠市蚌埠铁路中学2023-2024学年高二下学期4月月考数学试题
名校
7 . 某迷宫有三个通道,进入迷宫的每个人都要经过一扇智能门.首次到达此门,系统会随机(即等可能)为你打开一个 通道,若是1号通道,则需要1小时走出迷宫;若是2号、3号通道,则分别需要2小时、3小时返回智能门.再次到达智能门时,系统会随机打开一个你未到过的通道,直至走完迷宫为止.令ξ表示走出迷宫所需的时间.求ξ的分布列.均值和方差.
您最近一年使用:0次
8 . 红铃虫是棉花的主要害虫之一,能对农作物造成严重伤害.每只红铃虫的平均产卵数 和平均温度
和平均温度 有关.现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.
有关.现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.
表中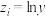 ,
,
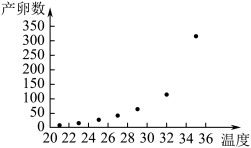
(1)根据散点图判断, 与
与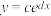 (其中
(其中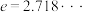 为自然对数的底数)哪一个更适宜作为平均产卵数
为自然对数的底数)哪一个更适宜作为平均产卵数 关于平均温度
关于平均温度 的回归方程类型?(给出判断即可不必说明理由)并由判断结果及表中数据,求出
的回归方程类型?(给出判断即可不必说明理由)并由判断结果及表中数据,求出 关于
关于 的回归方程.(计算结果精确到小数点后第三位)
的回归方程.(计算结果精确到小数点后第三位)
(2)根据以往统计,该地每年平均温度达到28℃以上时红铃虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治,记该地每年平均温度达到28℃以上的概率为 .
.
(ⅰ)记该地今后5年中,恰好需要3次人工防治的概率为 ,求
,求 的最大值,并求出相应的概率
的最大值,并求出相应的概率 .
.
(ⅱ)当 取最大值时,记该地今后5年中,需要人工防治的次数为
取最大值时,记该地今后5年中,需要人工防治的次数为 ,求
,求 的数学期望和方差.
的数学期望和方差.
附:对于一组数据 ,其回归直线
,其回归直线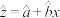 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: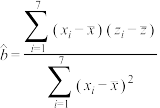 ,
,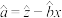 .
.
 和平均温度
和平均温度 有关.现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.
有关.现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.平均温度 /℃ /℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 | |||||
平均产卵数 /个 /个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 | |||||
 |  |  |  | 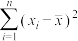 | ||||||||
| 27.429 | 81.286 | 3.612 | 40.182 | 147.714 | ||||||||
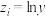 ,
,

(1)根据散点图判断,
 与
与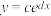 (其中
(其中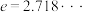 为自然对数的底数)哪一个更适宜作为平均产卵数
为自然对数的底数)哪一个更适宜作为平均产卵数 关于平均温度
关于平均温度 的回归方程类型?(给出判断即可不必说明理由)并由判断结果及表中数据,求出
的回归方程类型?(给出判断即可不必说明理由)并由判断结果及表中数据,求出 关于
关于 的回归方程.(计算结果精确到小数点后第三位)
的回归方程.(计算结果精确到小数点后第三位)(2)根据以往统计,该地每年平均温度达到28℃以上时红铃虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治,记该地每年平均温度达到28℃以上的概率为
 .
.(ⅰ)记该地今后5年中,恰好需要3次人工防治的概率为
 ,求
,求 的最大值,并求出相应的概率
的最大值,并求出相应的概率 .
.(ⅱ)当
 取最大值时,记该地今后5年中,需要人工防治的次数为
取最大值时,记该地今后5年中,需要人工防治的次数为 ,求
,求 的数学期望和方差.
的数学期望和方差.附:对于一组数据
 ,其回归直线
,其回归直线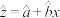 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: ,
,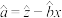 .
.
您最近一年使用:0次
2020-12-06更新
|
1137次组卷
|
15卷引用:2020届山东省日照第一中学高三上学期期中数学试题
2020届山东省日照第一中学高三上学期期中数学试题2020届海南省海口市海南中学高三第六次月考试卷数学2019届湖北省黄冈中学、华师一附中、襄阳四中、襄阳五中、荆州中学等八校高三第二次联考数学(理)试题广东省深圳外国语学校2020届高三下学期第6次月考数学(理)试题广东省汕头市金山中学2019-2020学年高二下学期6月月考数学试题(已下线)痛点16 概率与统计中的综合问题-2021年新高考数学一轮复习考点扫描(已下线)第十一单元 概率与统计(B卷 滚动提升检测)-2021年高考数学(理)一轮复习单元滚动双测卷河北正定中学2021届高三上学期第三次半月考数学试题安徽省六校教育研究会2021届高三下学期2月第二次联考理科数学试题(已下线)8.2 一元线性回归模型及其应用(精练)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)(已下线)黄金卷02-【赢在高考·黄金20卷】备战2021年高考数学全真模拟卷(山东高考专用)(已下线)专题23 概率与统计相结合问题(讲)-2021年高三数学二轮复习讲练测(新高考版)(已下线)专题27 概率与统计相结合问题(讲)-2021年高三数学二轮复习讲练测(文理通用)安徽省六安市舒城中学2021届高三下学期高考仿真(一)理科数学试题(已下线)第八章 成对数据的统计分析(选拔卷)-【单元测试】2021-2022学年高二数学尖子生选拔卷(人教A版2019选择性必修第三册)
解题方法
9 . 某袋中装有大小相同质地均匀的5个球,其中3个黑球和2个白球.从袋中随机取出2个球,记取出白球的个数为 ,
,
(1)求 的概率即
的概率即
(2)求取出白球的数学期望 和方差
和方差
 ,
,(1)求
 的概率即
的概率即
(2)求取出白球的数学期望
 和方差
和方差
您最近一年使用:0次
2020-12-03更新
|
1000次组卷
|
9卷引用:浙江省金华市曙光学校2020-2021学年高三上学期期中数学试题
浙江省金华市曙光学校2020-2021学年高三上学期期中数学试题人教B版(2019) 选修第二册 过关检测 第四章 4.2.4 随机变量的数字特征 课时2人教A版(2019) 选修第三册 实战演练 第七章 7.3 课时练习12 离散型随机变量的方差(已下线)专题2 离散型随机变量的分布列、均值与方差-学会解题之高三数学321训练体系【2022版】(已下线)考点27 随机变量的分布列、期望与方差(核心考点讲与练)-2023年高考数学一轮复习核心考点讲与练(新高考专用)(已下线)7.3.2离散型随机变量的方差(精讲)(已下线)7.3.2 离散型随机变量的方差(1)(已下线)7.3.2离散型随机变量的方差 (分层作业)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第三册)(已下线)8.2 离散型随机变量及其分布列(2)
10 . 某地区为了解党员同志每天的学习强国的积分情况,抽取了20名同志,其中男同志10名,女同志10名,他们的积分用茎叶图表示如下:积分在40分(含40分)以上的为积极学习的党员同志.
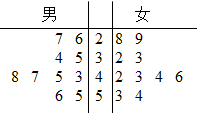
(1)求出男同志学习强国积分的平均值和女同志积极学习的频率,
(2)用频率估计概率,从该地区随机抽取3名党员,设积极学习的党员同志人数为 ,求
,求 的数学期望和方差.
的数学期望和方差.

(1)求出男同志学习强国积分的平均值和女同志积极学习的频率,
(2)用频率估计概率,从该地区随机抽取3名党员,设积极学习的党员同志人数为
 ,求
,求 的数学期望和方差.
的数学期望和方差.
您最近一年使用:0次
2020-07-28更新
|
246次组卷
|
2卷引用:广东省地市级2019-2020学年高二(下)期末数学试题




