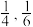 ;1小时以上且不超过2小时离开的概率分别为
;1小时以上且不超过2小时离开的概率分别为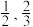 ;两人滑雪时间都不会超过3小时.
;两人滑雪时间都不会超过3小时.(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与均值E(ξ),方差D(ξ).
2 . 某纺织厂为了生产一种高端布料,准备从A农场购进一批优质棉花,厂方技术员从A农场存储的优质棉花中随机抽取了100处棉花,分别测量了其纤维长度(单位:mm)的均值,收集到100个样本数据,并制成如下频数分布表:
长度(单位:mm) | [23,25) | [25,27) | [27,29) | [29,31) | [31,33) | [33,35) | [35,37) | [37,39] |
频数 | 4 | 9 | 16 | 24 | 18 | 14 | 10 | 5 |
(1)求这100个样本数据的平均数
 和样本方差
和样本方差 (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);(2)将收集到的数据绘成直方图可以认为这批棉花的纤维长度服从分布
 其中
其中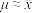 ,
,
①利用正态分布,求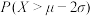 ;
;
②纺织厂将A农场送来的这批优质棉进行二次检验,从中随机抽取20处测量其纤维均值yi(i=1,2…,20),数据如下:
y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | y9 | y10 |
24.1 | 31.8 | 32.7 | 28.2 | 28.4 | 34.3 | 29.1 | 34.8 | 37.2 | 30.8 |
y11 | y12 | y13 | y14 | y15 | y16 | y17 | y18 | y19 | y20 |
30.6 | 25.2 | 32.9 | 27.1 | 35.9 | 28.9 | 33.9 | 29.5 | 35.0 | 29.9 |
若20个样本中纤维均值 的频率不低于①中
的频率不低于①中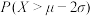 即可判断该批优质棉花合格,否则认为农场运送时掺杂了次品,判断该批棉花不合格.按照此依据判断A农场送来的这批棉花是否为合格的优质棉花,并说明理由.
即可判断该批优质棉花合格,否则认为农场运送时掺杂了次品,判断该批棉花不合格.按照此依据判断A农场送来的这批棉花是否为合格的优质棉花,并说明理由.
附:若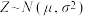 ,则
,则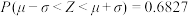 ,
,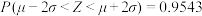 ,
,
(1)若水果店一天购进16个西瓜,求当天的利润
 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:个,
(单位:个, )的函数解析式;
)的函数解析式;(2)水果店记录了100天西瓜的日需求量(单位:个),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①若水果店一天购进16个西瓜,
 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求 的分布列、数学期望及方差;
的分布列、数学期望及方差;②若水果店计划一天购进16个或17个西瓜,你认为应购进16个还是17个?请说明理由.
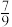 和
和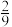 .项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利50%,也可能亏损30%,也可能不赔不赚,且这三种情况发生的概率分别为
.项目二:通信设备.据市场调研,投资到该项目上,到年底可能获利50%,也可能亏损30%,也可能不赔不赚,且这三种情况发生的概率分别为 ,
, ,
, .
.(1)针对以上两个投资项目,请你为投资公司选择一个合理的项目,并说明理由;
(2)若市场预期不变,该投资公司按照你选择的项目长期投资(每一年的利润和本金继续用作投资),问大约在哪一年的年底总资产(利润+本金)可以翻一番?(参考数据:
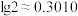 ,
,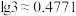 )
)
 ,乙种瓷砖的标准规格长宽为
,乙种瓷砖的标准规格长宽为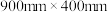 ,根据长期的检测结果,两种规格瓷砖每片的重量
,根据长期的检测结果,两种规格瓷砖每片的重量 (单位:
(单位: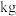 )都服从正态分布
)都服从正态分布 ,重量在
,重量在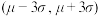 之外的瓷砖为废品,废品销毁不流入市场,其他重量的瓷砖为正品.
之外的瓷砖为废品,废品销毁不流入市场,其他重量的瓷砖为正品.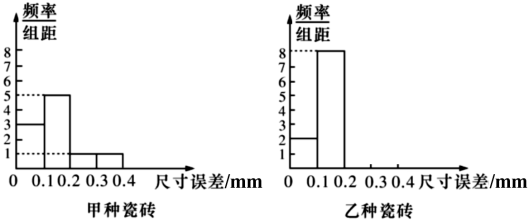
(1)在该陶瓷厂生产的瓷砖中随机抽取10片进行检测,求至少有1片为废品的概率;
(2)监管部门规定瓷砖长宽规格“尺寸误差”的计算方式如下:若瓷砖的实际长宽为
 ,
, ,标准长宽为
,标准长宽为 ,
, ,则“尺寸误差”为
,则“尺寸误差”为 ,按行业生产标准,其中“一级品”“二级品”“合格品”的“尺寸误差”的范围分别是
,按行业生产标准,其中“一级品”“二级品”“合格品”的“尺寸误差”的范围分别是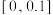 ,
, ,
,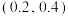 (正品瓷砖中没有“尺寸误差”大于
(正品瓷砖中没有“尺寸误差”大于 的瓷砖),现分别从甲、乙两种产品的正品中随机抽取各100片,分别进行“尺寸误差”的检测,统计后,绘制其频率分布直方图如图所示,已知经销商经营甲种瓷砖每片“一级品”的利润率为0.12,“二级品”的利润率为0.08,“合格品”的利润率为0.02.经销商经营乙种瓷砖每片“一级品”的利润率为0.10,“二级品”的利润率为0.05,“合格品”的利润率为0.02.视频率为概率.
的瓷砖),现分别从甲、乙两种产品的正品中随机抽取各100片,分别进行“尺寸误差”的检测,统计后,绘制其频率分布直方图如图所示,已知经销商经营甲种瓷砖每片“一级品”的利润率为0.12,“二级品”的利润率为0.08,“合格品”的利润率为0.02.经销商经营乙种瓷砖每片“一级品”的利润率为0.10,“二级品”的利润率为0.05,“合格品”的利润率为0.02.视频率为概率.①若经销商在甲、乙两种瓷砖上各投资10万元,
 和
和 分别表示投资甲、乙两种瓷砖所获得的利润,求
分别表示投资甲、乙两种瓷砖所获得的利润,求 和
和 的数学期望和方差,并由此分析经销商经销两种瓷砖的利弊;
的数学期望和方差,并由此分析经销商经销两种瓷砖的利弊;②若经销商在甲、乙两种瓷砖上总投资10万元,则分别在甲、乙两种瓷砖上投资多少万元时,可使得投资所获利润的方差和最小?
附:若随机变量
 服从正态分布
服从正态分布 ,则
,则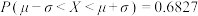 ,
,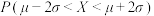
 ,
,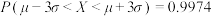 ,
, ,
,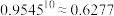 ,
,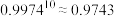
 ,从乙口袋中也取出3个球,记黑球个数为
,从乙口袋中也取出3个球,记黑球个数为 .
.(1)求
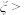
 时的概率;
时的概率;(2)若
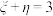 ,求随机变量
,求随机变量 的数学期望
的数学期望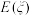 及
及 的方差
的方差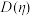 .
.
(1)求3个旅游团选择3条不同的线路的概率;
(2)求选择甲线路旅游团数的分布列、均值
 及方差.
及方差.
 、
、 、
、 、
、 、
、 五个不同的社团组织,为培养学生的兴趣爱好,要求每个学生必须且只能参加一个社团,假定某寝室的甲、乙、丙三名学生对这五个社团的选择是等可能的.
五个不同的社团组织,为培养学生的兴趣爱好,要求每个学生必须且只能参加一个社团,假定某寝室的甲、乙、丙三名学生对这五个社团的选择是等可能的.(1)求甲、乙、丙三名学生中至少有两人参加同一社团的概率;
(2)设随机变量
 为甲、乙、丙这三个学生参加
为甲、乙、丙这三个学生参加 或
或 社团的人数,求
社团的人数,求 的分布列、数学期望及方差.
的分布列、数学期望及方差.
| 测试1 | 测试2 | 测试3 | 测试4 | 测试5 | 测试6 | 测试7 | 测试8 | 测试9 | 测试10 | 测试11 | 测试12 | |
| 品牌A | 3 | 6 | 9 | 10 | 4 | 1 | 12 | 17 | 4 | 6 | 6 | 14 |
| 品牌B | 2 | 8 | 5 | 4 | 2 | 5 | 8 | 15 | 5 | 12 | 10 | 21 |
| 卫生习惯 | 垃圾处理 | 体育锻炼 | 心理健康 | 膳食合理 | 作息规律 | |
| 有效答卷份数 | 380 | 550 | 330 | 410 | 400 | 430 |
| 习惯良好频率 | 0.6 | 0.9 | 0.8 | 0.7 | 0.65 | 0.6 |
(1)从该小组收集的有效答卷中随机选取1份,求这份试卷的调查结果是“垃圾处理”中习惯良好者的概率;
(2)从“体育锻炼”和“心理健康”两类中各随机选取一份,估计恰有一份是具有良好习惯的概率;
(3)利用上述六类习惯调查的排序,即“卫生习惯”是第一类,“垃圾处理”是第二类
 “作息规律”是第六类用“
“作息规律”是第六类用“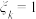 ”表示任选一位第
”表示任选一位第 类受访者是习惯良好者,“
类受访者是习惯良好者,“ ”表示任选一位第
”表示任选一位第 类受访者不是习惯良好者
类受访者不是习惯良好者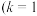 ,2,3,4,5,
,2,3,4,5,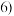 .求出方差
.求出方差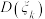 ,
,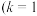 ,2,3,4,5,
,2,3,4,5,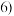 ,并由小到大排序.
,并由小到大排序.



