解题方法
1 . 某校举行知识竞赛,每个班各派5名同学参赛,若某班5名同学失分(均为整数)都不超过5分,则该班级为“优秀班级”.
(1)若A班5名同学失分分别为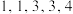 ,从这5个失分中随机抽两个分数记这两个分数差的绝对值为随机变量
,从这5个失分中随机抽两个分数记这两个分数差的绝对值为随机变量 ,求随机变量
,求随机变量 的分布列和期望.
的分布列和期望.
(2)若B班中5名同学失分的平均数为2,方差为2,问B班是否为优秀班级?说明理由.
(1)若A班5名同学失分分别为
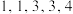 ,从这5个失分中随机抽两个分数记这两个分数差的绝对值为随机变量
,从这5个失分中随机抽两个分数记这两个分数差的绝对值为随机变量 ,求随机变量
,求随机变量 的分布列和期望.
的分布列和期望.(2)若B班中5名同学失分的平均数为2,方差为2,问B班是否为优秀班级?说明理由.
您最近一年使用:0次
名校
解题方法
2 . 已知首项为1的数列 满足
满足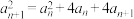 .
.
(1)若 ,在所有
,在所有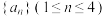 中随机抽取2个数列,记满足
中随机抽取2个数列,记满足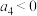 的数列
的数列 的个数为
的个数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 ;
;
(2)若数列 满足:若存在
满足:若存在 ,则存在
,则存在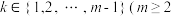 且
且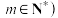 ,使得
,使得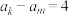 .
.
(i)若 ,证明:数列
,证明:数列 是等差数列,并求数列
是等差数列,并求数列 的前
的前 项和
项和 ;
;
(ii)在所有满足条件的数列 中,求使得
中,求使得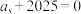 成立的
成立的 的最小值.
的最小值.
 满足
满足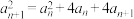 .
.(1)若
 ,在所有
,在所有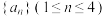 中随机抽取2个数列,记满足
中随机抽取2个数列,记满足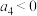 的数列
的数列 的个数为
的个数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 ;
;(2)若数列
 满足:若存在
满足:若存在 ,则存在
,则存在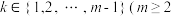 且
且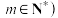 ,使得
,使得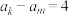 .
.(i)若
 ,证明:数列
,证明:数列 是等差数列,并求数列
是等差数列,并求数列 的前
的前 项和
项和 ;
;(ii)在所有满足条件的数列
 中,求使得
中,求使得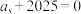 成立的
成立的 的最小值.
的最小值.
您最近一年使用:0次
2024-09-08更新
|
443次组卷
|
2卷引用:江西省九江市稳派联考2024-2025学年高三上学期开学数学试题
3 . 马尔科夫链是概率统计中的一个重要模型,其过程具备“无记忆”的性质:下一状态的概率分布只能由当前状态决定,即第n+1次状态的概率分布只与第n次的状态有关,与第 ,…次的状态无关,即
,…次的状态无关,即 .已知甲盒中装有1个白球和2个黑球,乙盒中装有2个白球,现从甲、乙两个盒中各任取1个球交换放入对方的盒中,重复n次(
.已知甲盒中装有1个白球和2个黑球,乙盒中装有2个白球,现从甲、乙两个盒中各任取1个球交换放入对方的盒中,重复n次( )这样的操作,记此时甲盒中白球的个数为
)这样的操作,记此时甲盒中白球的个数为 ,甲盒中恰有2个白球的概率为
,甲盒中恰有2个白球的概率为 ,恰有1个白球的概率为
,恰有1个白球的概率为 .
.
(1)求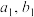 和
和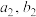 .
.
(2)证明: 为等比数列.
为等比数列.
(3)求 的数学期望(用n表示).
的数学期望(用n表示).
 ,…次的状态无关,即
,…次的状态无关,即 .已知甲盒中装有1个白球和2个黑球,乙盒中装有2个白球,现从甲、乙两个盒中各任取1个球交换放入对方的盒中,重复n次(
.已知甲盒中装有1个白球和2个黑球,乙盒中装有2个白球,现从甲、乙两个盒中各任取1个球交换放入对方的盒中,重复n次( )这样的操作,记此时甲盒中白球的个数为
)这样的操作,记此时甲盒中白球的个数为 ,甲盒中恰有2个白球的概率为
,甲盒中恰有2个白球的概率为 ,恰有1个白球的概率为
,恰有1个白球的概率为 .
.(1)求
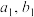 和
和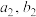 .
.(2)证明:
 为等比数列.
为等比数列.(3)求
 的数学期望(用n表示).
的数学期望(用n表示).
您最近一年使用:0次
2024-09-02更新
|
342次组卷
|
4卷引用:江西省部分学校2024-2025学年高三上学期开学第一次月考数学试卷
江西省部分学校2024-2025学年高三上学期开学第一次月考数学试卷(已下线)重难点突破03 高等背景下概率论新定义(七大题型)(已下线)重难点突破01 概率与统计的综合问题(十八大题型)福建省德化第二中学2024-2025学年高三上学期第一阶段考试(10月)数学试题
4 . 高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.每次试验时,让一个小球从高尔顿板上方的通道口落下,小球在下落过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内,在如图所示的小木块中,上面10层为高尔顿板,最下面为球槽.小球从通道口落下,第一次与第2层中间的小木块碰撞,以 的概率向左或向右滚下,依次经过9次与小木块碰撞,最后掉编号(从左至右)为1,2,…,10的球槽内.若一次试验中小球滚落至事先选定的球槽编号n即得积分
的概率向左或向右滚下,依次经过9次与小木块碰撞,最后掉编号(从左至右)为1,2,…,10的球槽内.若一次试验中小球滚落至事先选定的球槽编号n即得积分 ,否则不得分.若
,否则不得分.若 ,则每次试验前选定球槽编号为
,则每次试验前选定球槽编号为______ ,所得积分的数学期望最大.
 的概率向左或向右滚下,依次经过9次与小木块碰撞,最后掉编号(从左至右)为1,2,…,10的球槽内.若一次试验中小球滚落至事先选定的球槽编号n即得积分
的概率向左或向右滚下,依次经过9次与小木块碰撞,最后掉编号(从左至右)为1,2,…,10的球槽内.若一次试验中小球滚落至事先选定的球槽编号n即得积分 ,否则不得分.若
,否则不得分.若 ,则每次试验前选定球槽编号为
,则每次试验前选定球槽编号为
您最近一年使用:0次
名校
解题方法
5 . 如图,一只蚂蚁从正方体 的顶点
的顶点 出发沿棱爬行,记蚂蚁从一个顶点到另一个顶点为一次爬行,每次爬行的方向是随机的,蚂蚁沿正方体上、下底面上的棱爬行的概率为
出发沿棱爬行,记蚂蚁从一个顶点到另一个顶点为一次爬行,每次爬行的方向是随机的,蚂蚁沿正方体上、下底面上的棱爬行的概率为 ,沿正方体的侧棱爬行的概率为
,沿正方体的侧棱爬行的概率为 .
.
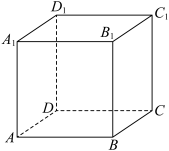
(1)若蚂蚁爬行5次,求蚂蚁在下底面顶点的概率;
(2)若蚂蚁爬行5次,记它在顶点 出现的次数为
出现的次数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
 的顶点
的顶点 出发沿棱爬行,记蚂蚁从一个顶点到另一个顶点为一次爬行,每次爬行的方向是随机的,蚂蚁沿正方体上、下底面上的棱爬行的概率为
出发沿棱爬行,记蚂蚁从一个顶点到另一个顶点为一次爬行,每次爬行的方向是随机的,蚂蚁沿正方体上、下底面上的棱爬行的概率为 ,沿正方体的侧棱爬行的概率为
,沿正方体的侧棱爬行的概率为 .
.
(1)若蚂蚁爬行5次,求蚂蚁在下底面顶点的概率;
(2)若蚂蚁爬行5次,记它在顶点
 出现的次数为
出现的次数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
您最近一年使用:0次
解题方法
6 . 农民专业合作社是在农村家庭承包经营的基础上,同类农产品的生产经营者或同类农业生产经营服务的提供者、利用者、自愿联合、民主管理的互助性经济组织,国家给予农民专业合作社在生产、经营、销售等方面全方位的优惠政策.某地大型农民专业合作社不断探索优化生产、经营、销售等方面的科学方案,引入人工智能管理系统,合作社的市场营销研究人员调研该合作社的10个主体项目,统计分析人工智能管理的实际经济收益 (单位:万元),与市场预测的经济收益
(单位:万元),与市场预测的经济收益 (单位:万元)的相关数据如下表:(注:10个主体项目号分别记为
(单位:万元)的相关数据如下表:(注:10个主体项目号分别记为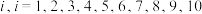 )
)
并计算得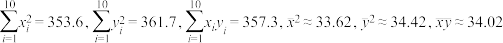
(1)求该合作预测收益 与实际收益
与实际收益 的样本相关系数(精确到0.01),并判断它们是否具有较强的线性相关关系;
的样本相关系数(精确到0.01),并判断它们是否具有较强的线性相关关系;
(2)规定:数组 满足
满足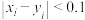 为“
为“ 类营销误差”;满足
类营销误差”;满足 为“
为“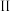 类营销误差”;满足
类营销误差”;满足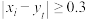 为“
为“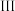 类营销误差”.为进一步研究,该合作社的市场营销研究人员从“
类营销误差”.为进一步研究,该合作社的市场营销研究人员从“ 类营销误差”,“
类营销误差”,“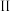 类营销误差”中随机抽取3组数据与“
类营销误差”中随机抽取3组数据与“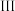 类营销误差”数据进行对比,记抽到“
类营销误差”数据进行对比,记抽到“ 类营销误差”的数据的组数为随机变量
类营销误差”的数据的组数为随机变量 .求
.求 的分布列与数学期望.
的分布列与数学期望.
附:相关系数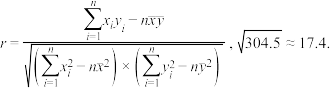 .
.
 (单位:万元),与市场预测的经济收益
(单位:万元),与市场预测的经济收益 (单位:万元)的相关数据如下表:(注:10个主体项目号分别记为
(单位:万元)的相关数据如下表:(注:10个主体项目号分别记为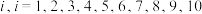 )
)项目号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
实际收益 | 5.38 | 7.99 | 6.37 | 6.71 | 7.53 | 5.53 | 4.18 | 4.04 | 6.02 | 4.23 |
预测收益 | 5.43 | 8.07 | 6.57 | 6.14 | 7.95 | 5.56 | 4.27 | 4.15 | 6.04 | 4.49 |
 | 0.05 | 0.08 | 0.2 | 0.57 | 0.42 | 0.03 | 0.09 | 0.11 | 0.02 | 0.26 |
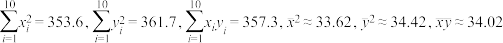
(1)求该合作预测收益
 与实际收益
与实际收益 的样本相关系数(精确到0.01),并判断它们是否具有较强的线性相关关系;
的样本相关系数(精确到0.01),并判断它们是否具有较强的线性相关关系;(2)规定:数组
 满足
满足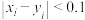 为“
为“ 类营销误差”;满足
类营销误差”;满足 为“
为“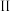 类营销误差”;满足
类营销误差”;满足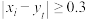 为“
为“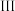 类营销误差”.为进一步研究,该合作社的市场营销研究人员从“
类营销误差”.为进一步研究,该合作社的市场营销研究人员从“ 类营销误差”,“
类营销误差”,“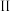 类营销误差”中随机抽取3组数据与“
类营销误差”中随机抽取3组数据与“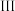 类营销误差”数据进行对比,记抽到“
类营销误差”数据进行对比,记抽到“ 类营销误差”的数据的组数为随机变量
类营销误差”的数据的组数为随机变量 .求
.求 的分布列与数学期望.
的分布列与数学期望.附:相关系数
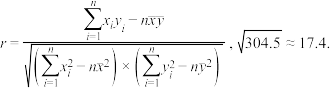 .
.
您最近一年使用:0次
2024-07-01更新
|
248次组卷
|
3卷引用:江西省萍乡市萍乡实验学校2025届高三上学期起点考试数学试卷
江西省萍乡市萍乡实验学校2025届高三上学期起点考试数学试卷湖南省娄底市2023-2024学年高三下学期高考考前仿真联考二数学试题(已下线)第四章 统计 专题二 统计相关性与回归分析 微点3 相关分析与回归分析(三)【培优版】
解题方法
7 . 2023年12月31日的下午,某班级在学校的多功能厅,以“庆元旦迎新年”为主题举办联欢会.为了鼓励班级的同学积极参与活动,组委会准备在联欢会上搞一个抽奖活动,凡是上台表演节目的同学最多有3次抽奖机会(没有上台表演的同学没有抽奖机会).每次抽中,可依次获得5元,10元,20元的礼品,若没有抽中,不可继续抽奖.每次抽中后,可以选择带走抽中的所有礼品,结束抽奖,也可选择继续抽奖,若没有抽中,则连同前面所得礼品全部归零,结束抽奖.已知参加本次抽奖活动的同学每次抽中的概率依次为 ,
, ,
, ,且每个同学选择继续抽奖的概率依次是
,且每个同学选择继续抽奖的概率依次是 和
和 .小张同学准备在这次活动中表演一个单口相声,并参与抽奖活动.
.小张同学准备在这次活动中表演一个单口相声,并参与抽奖活动.
(1)求小张同学第一次抽中但最终所得礼品归零的概率;
(2)设小张同学所得礼品的金额总数为随机变量X,求X的分布列和数学期望;
(3)组委会已经筹集到用于购买礼品的专项资金200元,如果当天有32名同学上台表演,问已经筹集到的专项资金是否够用?
您最近一年使用:0次
名校
8 . 甲盒中装有3个蓝球、2个黄球,乙盒中装有2个蓝球、3个黄球,同时从甲、乙两盒中取出 个球交换,分别记交换后甲、乙两个盒子中蓝球个数的数学期望为
个球交换,分别记交换后甲、乙两个盒子中蓝球个数的数学期望为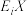 ,
, ,则下列结论正确的是( )
,则下列结论正确的是( )
 个球交换,分别记交换后甲、乙两个盒子中蓝球个数的数学期望为
个球交换,分别记交换后甲、乙两个盒子中蓝球个数的数学期望为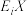 ,
, ,则下列结论正确的是( )
,则下列结论正确的是( )A.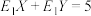 | B. |
C.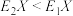 | D. |
您最近一年使用:0次
2024-03-08更新
|
466次组卷
|
6卷引用:江西省部分学校2023-2024学年高二下学期开学考试数学试题
江西省部分学校2023-2024学年高二下学期开学考试数学试题(已下线)8.2 离散型随机变量及其分布列(4)河北省沧州市运东四校联考2023-2024学年高二下学期4月期中考试数学试题河北省石家庄市赵县河北赵县中学、高邑县第一中学、无极中学2023-2024学年高二下学期4月月考考试检测数学试题(已下线)专题06 离散型随机变量与正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)山西省大同市灵丘豪洋中学2023-2024学年高二下学期5月质量检测数学试卷
名校
解题方法
9 . 有 双鞋子,每双标记上数字
双鞋子,每双标记上数字 、
、 、
、 、
、 、
、 ,从中取
,从中取 只鞋子.
只鞋子.
(1)求取出的 只鞋子都没有成对的概率;
只鞋子都没有成对的概率;
(2)记取出的 只鞋子的最大数字为
只鞋子的最大数字为 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.
 双鞋子,每双标记上数字
双鞋子,每双标记上数字 、
、 、
、 、
、 、
、 ,从中取
,从中取 只鞋子.
只鞋子.(1)求取出的
 只鞋子都没有成对的概率;
只鞋子都没有成对的概率;(2)记取出的
 只鞋子的最大数字为
只鞋子的最大数字为 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.
您最近一年使用:0次
2024-02-28更新
|
519次组卷
|
4卷引用:江西省红色十校2024届高三下学期2月联考数学试卷
江西省红色十校2024届高三下学期2月联考数学试卷江西省部分学校2024届高三下学期3月月考数学试题(已下线)7.3.1离散型随机变量的均值(分层练习,6大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)广东省珠海市第二中学2024届高三下学期3月月考数学试题
名校
10 . 2024年1月5日起,第40届中国·哈尔滨国际冰雪节在黑龙江省哈尔滨市举行.让大家对冰雪文化进一步了解,激发了大家对冰雪运动进一步的热爱.为了调查不同年龄层的人对“冰雪运动”的喜爱态度.某研究小组随机调查了哈尔滨市M社区年龄在 的市民300人,所得结果统计如下频数分布表所示
的市民300人,所得结果统计如下频数分布表所示
(1)求该样本中市民年龄的平均数;(同一组中的数据用该区间的中点值作代表)
(2)从这300名市民中随机抽取1人,在此人喜爱冰雪运动的前提下,求其年龄小于50周岁的概率:
(3)为鼓励市民积极参加这次调查,该研究小组决定给予参加调查的市民一定的奖励,奖励方案有两种:
方案一:按年龄a进行分类奖励,当 时,奖励10元:当
时,奖励10元:当 时,奖励30元:当
时,奖励30元:当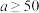 时,奖励40元;
时,奖励40元;
方案二:利用抽奖的方式获得奖金,其中年龄低于样本中位数的可抽1次奖,年龄不低于样本中位数的可抽2次奖.每次抽中奖励30元,未抽中奖励10元,各次抽奖间相互独立,且每次抽奖中奖的概率均为 ,
,
将频率视为概率,利用样本估计总体的思想,若该研究小组希望最终发出更多的奖金,则从期望角度出发.该研究小组应采取哪种方案
 的市民300人,所得结果统计如下频数分布表所示
的市民300人,所得结果统计如下频数分布表所示年龄 (单位:周岁) (单位:周岁) | 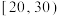 | 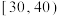 |  | 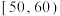 | 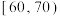 |
| 频数 | 30 | 81 | 99 | 60 | 30 |
| 持喜爱态度 | 24 | 65 | 75 | 30 | 12 |
(1)求该样本中市民年龄的平均数;(同一组中的数据用该区间的中点值作代表)
(2)从这300名市民中随机抽取1人,在此人喜爱冰雪运动的前提下,求其年龄小于50周岁的概率:
(3)为鼓励市民积极参加这次调查,该研究小组决定给予参加调查的市民一定的奖励,奖励方案有两种:
方案一:按年龄a进行分类奖励,当
 时,奖励10元:当
时,奖励10元:当 时,奖励30元:当
时,奖励30元:当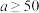 时,奖励40元;
时,奖励40元;方案二:利用抽奖的方式获得奖金,其中年龄低于样本中位数的可抽1次奖,年龄不低于样本中位数的可抽2次奖.每次抽中奖励30元,未抽中奖励10元,各次抽奖间相互独立,且每次抽奖中奖的概率均为
 ,
,将频率视为概率,利用样本估计总体的思想,若该研究小组希望最终发出更多的奖金,则从期望角度出发.该研究小组应采取哪种方案
您最近一年使用:0次
2024-02-28更新
|
534次组卷
|
2卷引用:江西省上进联盟2024届高三下学期一轮总复习(开学考)验收考试数学试卷



