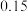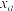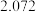1 . 袋中有10个大小相同的球,其中6个黑球,4个白球,现从中任取4个球,记随机变量X为其中白球的个数,随机变量Y为其中黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量Z为取出4个球的总得分,则下列结论中正确的是( )
A.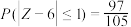 | B. |
C. | D.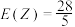 |
您最近一年使用:0次
2022-05-31更新
|
2688次组卷
|
9卷引用:江苏省南京师范大学附属中学2021-2022学年高二下学期期末模拟数学试题
江苏省南京师范大学附属中学2021-2022学年高二下学期期末模拟数学试题湖北省华中师大一附中2022届高三下学期高考前测试数学试题(已下线)专题34 随机变量及其分布列(针对训练)-2023年高考一轮复习精讲精练宝典(新高考专用)(已下线)7.4.2 超几何分布 (精练)江苏省南通市海安高级中学2024届高三上学期1月学情调研数学试题(已下线)专题20 概率与统计常考小题归类(15大题型)(练习)(已下线)第07讲 7.4.2超几何分布-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)7.4.2 超几何分布——课后作业(提升版)新疆兵团第三师图木舒克市鸿德实验学校2023-2024学年高二下学期第二次月考数学试卷
名校
2 . 某城市人口数量950万人左右,共900个社区.在实施垃圾分类之前,随机抽取300个社区,并对这300个社区某天产生的垃圾量(单位:吨)进行了调查,每个社区在这一天的垃圾量X大致服从正态分布 .将垃圾量超过32吨
.将垃圾量超过32吨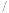 天的社区确定为“超标”社区.
天的社区确定为“超标”社区.
(1)请利用正态分布知识估计这900个社区中“超标”社区的个数;(结果取整数部分)
(2)通过研究样本原始数据发现,抽取的300个社区中这一天共有7个“超标”社区,市政府决定对7个“超标”社区的垃圾来源进行跟踪调查.现计划在这7个“超标”社区中任取4个进行跟踪调查,已知这7个社区中有3个社区在这一天的垃圾量超过35吨.设 为抽到的这一天的垃圾量超过35吨的社区个数,求
为抽到的这一天的垃圾量超过35吨的社区个数,求 的概率分布与数学期望;
的概率分布与数学期望;
(3)用样本的频率代替总体的概率,现从该市所有社区中随机抽取50个社区,记 为这一天垃圾量超过32吨的小区的个数,求
为这一天垃圾量超过32吨的小区的个数,求 的值.
的值.
(参考数据: ;
;  ;
; ;
; )
)
 .将垃圾量超过32吨
.将垃圾量超过32吨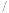 天的社区确定为“超标”社区.
天的社区确定为“超标”社区.(1)请利用正态分布知识估计这900个社区中“超标”社区的个数;(结果取整数部分)
(2)通过研究样本原始数据发现,抽取的300个社区中这一天共有7个“超标”社区,市政府决定对7个“超标”社区的垃圾来源进行跟踪调查.现计划在这7个“超标”社区中任取4个进行跟踪调查,已知这7个社区中有3个社区在这一天的垃圾量超过35吨.设
 为抽到的这一天的垃圾量超过35吨的社区个数,求
为抽到的这一天的垃圾量超过35吨的社区个数,求 的概率分布与数学期望;
的概率分布与数学期望;(3)用样本的频率代替总体的概率,现从该市所有社区中随机抽取50个社区,记
 为这一天垃圾量超过32吨的小区的个数,求
为这一天垃圾量超过32吨的小区的个数,求 的值.
的值.(参考数据:
 ;
;  ;
; ;
; )
)
您最近一年使用:0次
2024-05-25更新
|
1180次组卷
|
4卷引用:江苏省南京市六校联合体学校2023-2024学年高二下学期5月月考数学试题
江苏省南京市六校联合体学校2023-2024学年高二下学期5月月考数学试题山东省菏泽市定陶区第一中学2023-2024学年高二下学期5月月考数学试题(已下线)专题06 离散型随机变量与正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)河北省唐县第一中学2023-2024学年高二下学期6月期末数学试题
名校
解题方法
3 . 下列命题中,正确的是( ).
A.随机变量X服从二项分布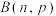 ,若 ,若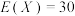 , ,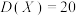 ,则 ,则 |
B.某投掷类游戏闯关规则是游戏者最多投掷5次,只要有一次投中,游戏者即闯关成功,并停止投掷,已知每次投中的概率为 ,则游戏者闯关成功的概率为 ,则游戏者闯关成功的概率为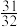 |
C.从3个红球2个白球中,一次摸出3个球,则摸出红球的个数X服从超几何分布,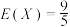 |
D.某人在10次射击中,击中目标的次数为X,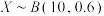 ,则当且仅当 ,则当且仅当 时概率最大 时概率最大 |
您最近一年使用:0次
2023-05-19更新
|
1042次组卷
|
8卷引用:江苏省南京田家炳高级中学2023-2024学年高二下学期5月月考数学试卷
名校
4 . 某省 年开始将全面实施新高考方案.在
年开始将全面实施新高考方案.在 门选择性考试科目中,物理、历史这两门科目采用原始分计分;思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为
门选择性考试科目中,物理、历史这两门科目采用原始分计分;思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为 ,
, ,
, ,
, ,
, 共
共 个等级,各等级人数所占比例分别为
个等级,各等级人数所占比例分别为 、
、 、
、 、
、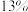 和
和 ,并按给定的公式进行转换赋分.该省组织了一次高一年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.
,并按给定的公式进行转换赋分.该省组织了一次高一年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.
(1)某校生物学科获得 等级的共有10名学生,其原始分及转换分如下表:
等级的共有10名学生,其原始分及转换分如下表:
现从这10名学生中随机抽取3人,设这3人中生物转换分不低于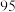 分的人数为
分的人数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)假设该省此次高一学生生物学科原始分 服从正态分布
服从正态分布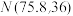 .若
.若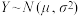 ,令
,令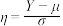 ,则
,则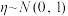 ,请解决下列问题:
,请解决下列问题:
①若以此次高一学生生物学科原始分 等级的最低分为实施分层教学的划线分,试估计该划线分大约为多少分?(结果保留为整数)
等级的最低分为实施分层教学的划线分,试估计该划线分大约为多少分?(结果保留为整数)
②现随机抽取了该省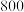 名高一学生的此次生物学科的原始分,若这些学生的原始分相互独立,记
名高一学生的此次生物学科的原始分,若这些学生的原始分相互独立,记 为被抽到的原始分不低于
为被抽到的原始分不低于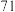 分的学生人数,求
分的学生人数,求 取得最大值时
取得最大值时 的值.
的值.
附:若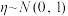 ,则
,则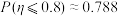 ,
, .
.
 年开始将全面实施新高考方案.在
年开始将全面实施新高考方案.在 门选择性考试科目中,物理、历史这两门科目采用原始分计分;思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为
门选择性考试科目中,物理、历史这两门科目采用原始分计分;思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为 ,
, ,
, ,
, ,
, 共
共 个等级,各等级人数所占比例分别为
个等级,各等级人数所占比例分别为 、
、 、
、 、
、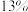 和
和 ,并按给定的公式进行转换赋分.该省组织了一次高一年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.
,并按给定的公式进行转换赋分.该省组织了一次高一年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.(1)某校生物学科获得
 等级的共有10名学生,其原始分及转换分如下表:
等级的共有10名学生,其原始分及转换分如下表:| 原始分 | 91 | 90 | 89 | 88 | 87 | 85 | 83 | 82 |
| 转换分 | 100 | 99 | 97 | 95 | 94 | 91 | 88 | 86 |
| 人数 | 1 | 1 | 2 | 1 | 2 | 1 | 1 | 1 |
现从这10名学生中随机抽取3人,设这3人中生物转换分不低于
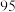 分的人数为
分的人数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(2)假设该省此次高一学生生物学科原始分
 服从正态分布
服从正态分布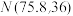 .若
.若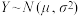 ,令
,令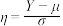 ,则
,则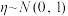 ,请解决下列问题:
,请解决下列问题:①若以此次高一学生生物学科原始分
 等级的最低分为实施分层教学的划线分,试估计该划线分大约为多少分?(结果保留为整数)
等级的最低分为实施分层教学的划线分,试估计该划线分大约为多少分?(结果保留为整数)②现随机抽取了该省
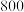 名高一学生的此次生物学科的原始分,若这些学生的原始分相互独立,记
名高一学生的此次生物学科的原始分,若这些学生的原始分相互独立,记 为被抽到的原始分不低于
为被抽到的原始分不低于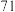 分的学生人数,求
分的学生人数,求 取得最大值时
取得最大值时 的值.
的值.附:若
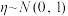 ,则
,则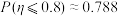 ,
, .
.
您最近一年使用:0次
2020-06-05更新
|
4521次组卷
|
17卷引用:江苏省南京市第十三中学2021-2022学年高二下学期初数学试题
江苏省南京市第十三中学2021-2022学年高二下学期初数学试题福州市2020届高三毕业班第三次质量检查理科数学试题江苏省苏州市2020-2021学年高三上学期9月期初调研数学试题山东省泰安市2019-2020学年下学期高二期末考试数学试题江苏省扬州市高邮市第一中学2020-2021学年高三上学期9月阶段性测试数学试题江苏省苏州市相城区陆慕高级中学2020-2021学年高三上学期期初数学试题(已下线)专题12 四大分布:两点分布、超几何分布、二项分布、正态分布-2021-2022学年高二数学下学期期末必考题型归纳及过关测试(人教A版2019)(已下线)专题14 概率、统计、期望(已下线)专题9-1 概率与统计及分布列归类(理)(讲+练)-1(已下线)第四篇 概率与统计 专题2 最可能成功次数 微点1 最可能成功次数广东省茂名市华南师范大学附属电白学校2023届高三下学期5月调研数学试题(已下线)第四篇 概率与统计 专题7 常见分布 微点2 其它分布2023年全国中学生数学能力测评(终评)高三年级组试题(已下线)结业测试卷(范围:第五、六、七章)(提高篇)-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)河南省南阳市2023-2024学年高二上学期期终质量评估数学试题(已下线)第1讲:二项式定理和二项分布的最值问题【练】(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点2 重要的概率分布模型(二)【基础版】
名校
解题方法
5 . 天文学上用星等表示星体亮度,星等的数值越小,星体越亮.视星等是指观测者用肉眼所看到的星体亮度;绝对星等是假定把恒星放在距地球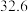 光年的地方测得的恒星的亮度,反映恒星的真实发光本领.下表列出了(除太阳外)视星等数值最小的10颗最亮恒星的相关数据,其中
光年的地方测得的恒星的亮度,反映恒星的真实发光本领.下表列出了(除太阳外)视星等数值最小的10颗最亮恒星的相关数据,其中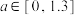 .
.
(1)从表中随机选择一颗恒星,求它的绝对星等的数值小于视星等的数值的概率;
(2)已知北京的纬度是北纬 ,当且仅当一颗恒星的“赤纬”数值大于
,当且仅当一颗恒星的“赤纬”数值大于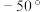 时,能在北京的夜空中看到它.现从这10颗恒星中随机选择4颗,记其中能在北京的夜空中看到的数量为
时,能在北京的夜空中看到它.现从这10颗恒星中随机选择4颗,记其中能在北京的夜空中看到的数量为 颗,求
颗,求 的分布列和数学期望;
的分布列和数学期望;
(3)记 时10颗恒星的视星等的方差为
时10颗恒星的视星等的方差为 ,记
,记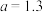 时10颗恒星的视星等的方差为
时10颗恒星的视星等的方差为 ,判断
,判断 与
与 之间的大小关系.(结论不需要证明)
之间的大小关系.(结论不需要证明)
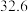 光年的地方测得的恒星的亮度,反映恒星的真实发光本领.下表列出了(除太阳外)视星等数值最小的10颗最亮恒星的相关数据,其中
光年的地方测得的恒星的亮度,反映恒星的真实发光本领.下表列出了(除太阳外)视星等数值最小的10颗最亮恒星的相关数据,其中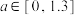 .
.| 星名 | 天狼星 | 老人星 | 南门二 | 大角星 | 织女一 | 五车二 | 参宿七 | 南河三 | 水委一 | 参宿四 |
| 视星等 | 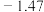 | 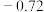 | 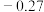 | 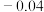 | 0.03 | 0.08 | 0.12 | 0.38 | 0.46 | a |
| 绝对星等 | 1.42 | 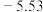 | 4.4 | 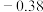 | 0.6 | 0.1 |  | 2.67 |  | 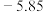 |
| 赤纬 |  | 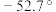 |  |  |  | 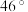 |  | 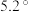 |  | 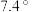 |
(2)已知北京的纬度是北纬
 ,当且仅当一颗恒星的“赤纬”数值大于
,当且仅当一颗恒星的“赤纬”数值大于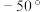 时,能在北京的夜空中看到它.现从这10颗恒星中随机选择4颗,记其中能在北京的夜空中看到的数量为
时,能在北京的夜空中看到它.现从这10颗恒星中随机选择4颗,记其中能在北京的夜空中看到的数量为 颗,求
颗,求 的分布列和数学期望;
的分布列和数学期望;(3)记
 时10颗恒星的视星等的方差为
时10颗恒星的视星等的方差为 ,记
,记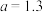 时10颗恒星的视星等的方差为
时10颗恒星的视星等的方差为 ,判断
,判断 与
与 之间的大小关系.(结论不需要证明)
之间的大小关系.(结论不需要证明)
您最近一年使用:0次
2021-04-07更新
|
2376次组卷
|
15卷引用:江苏省南京市天印高级中学2021--2022学年高二下学期期中数学试题
江苏省南京市天印高级中学2021--2022学年高二下学期期中数学试题北京市西城区2021届高三一模数学试题陕西省宝鸡市千阳县中学2021届高三下学期5月第十一次模考理科数学试题人教B版(2019) 选修第二册 名师精选 第四章 概率与 统计苏教版(2019) 选修第二册 限时训练 第26练 离散型随机变量的方差与标准差北京市第十三中学2022届高三12月月考数学试题陕西省西安中学2022届高三下学期二模理科数学试题北京市第五十七中学2021-2022学年高二6月月考数学试题(已下线)专题3超几何分布运算(提升版)北京市第十一中学2023届高三上学期11月月考数学试题北京市西城区北京师范大学附属中学2022-2023学年高三上学期12月月考数学试题北京市昌平区第二中学2022-2023学年高二下学期期中数学模拟练习试题北京市第一七一中学2024届高三上学期开学考试数学试题北京高二专题12概率与统计(第二部分)【巩固卷】第7章 概率初步(续)单元测试B沪教版(2020)选择性必修第二册
6 . 一个袋中装有除颜色外其余完全相同的6个黑球和4个白球,现从中任取4个小球,设取出的4个小球中白球的个数为 ,则( )
,则( )
 ,则( )
,则( )A.随机变量 服从二项分布 服从二项分布 | B.随机变量 服从超几何分布 服从超几何分布 |
C.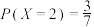 | D.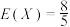 |
您最近一年使用:0次
2021-09-20更新
|
2235次组卷
|
16卷引用:江苏省南京市金陵中学2020-2021学年高二下学期期初学情调研数学试题
江苏省南京市金陵中学2020-2021学年高二下学期期初学情调研数学试题湖南省三湘名校联盟2020-2021学年高三上学期元月第五次联考数学试题(已下线)【新教材精创】7.4.2超几何分布 -A基础练江苏省盐城市阜宁中学2020-2021学年高二下学期期中数学试题辽宁省锦州市第二高级中学2020-2021学年高二下学期期中考试数学试题人教B版(2019) 选修第二册 突围者 第四章 第二节课时4 随机变量的数字特征苏教版(2019) 选修第二册 限时训练 第30练 概率章综合检测苏教版(2019) 选修第二册 限时训练 第28练 超几何分布(已下线)7.4二项分布和超几何分布C卷人教A版(2019) 选修第三册 核心素养 6-8章 阶段检测卷人教A版(2019) 选修第三册 过关斩将 第七章 专题强化练7广东省汕头市东厦中学、汕头市达濠华侨中学2021-2022学年高二下学期阶段二考数学试题山东省滨州高新高级中学2022-2023学年高二下学期4月月考数学试题河北省石家庄北华中学2022-2023学年高二下学期6月月考数学试题广东省肇庆市肇庆鼎湖中学2023-2024学年高二下学期5月月考数学试题江西省上饶市广丰区洋口中学2022-2023学年高二上学期第三次月考数学试题
名校
7 . 学史明理,学史增信,学史崇德,学史力行.近年来,某市积极组织开展党史学习教育的活动,为调查活动开展的效果,市委宣传部对全市多个基层支部的党员进行了测试,并从中抽取了1000份试卷进行调查,根据这1000份试卷的成绩(单位:分,满分100分)得到如下频数分布表:
(1)求这1000份试卷成绩的平均数?(同一组中的数据用该组区间的中点值为代表).
(2)假设此次测试的成绩 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数,
近似为样本平均数, 近似为样本方差
近似为样本方差 ,已知
,已知 的近似值为6.61,以样本估计总体,假设有84.14%的学生的测试成绩高于市教育局预期的平均成绩,则市教育局预期的平均成绩大约为多少(结果保留一位小数)?
的近似值为6.61,以样本估计总体,假设有84.14%的学生的测试成绩高于市教育局预期的平均成绩,则市教育局预期的平均成绩大约为多少(结果保留一位小数)?
(3)该市教育局准备从成绩在 内的120份试卷中用分层抽样的方法抽取6份,再从这6份试卷中随机抽取3份进行进一步分析,记
内的120份试卷中用分层抽样的方法抽取6份,再从这6份试卷中随机抽取3份进行进一步分析,记 为抽取的3份试卷中测试成绩在
为抽取的3份试卷中测试成绩在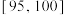 内的份数,求
内的份数,求 的分布列和数学期望.
的分布列和数学期望.
参考数据:若 ,则
,则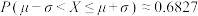 ,
,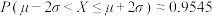 ,
,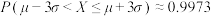 .
.
| 成绩/分 | 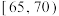 | 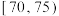 | 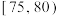 |  |  | 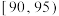 | 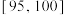 |
| 频数 | 40 | 90 | 200 | 400 | 150 | 80 | 40 |
(2)假设此次测试的成绩
 服从正态分布
服从正态分布 ,其中
,其中 近似为样本平均数,
近似为样本平均数, 近似为样本方差
近似为样本方差 ,已知
,已知 的近似值为6.61,以样本估计总体,假设有84.14%的学生的测试成绩高于市教育局预期的平均成绩,则市教育局预期的平均成绩大约为多少(结果保留一位小数)?
的近似值为6.61,以样本估计总体,假设有84.14%的学生的测试成绩高于市教育局预期的平均成绩,则市教育局预期的平均成绩大约为多少(结果保留一位小数)?(3)该市教育局准备从成绩在
 内的120份试卷中用分层抽样的方法抽取6份,再从这6份试卷中随机抽取3份进行进一步分析,记
内的120份试卷中用分层抽样的方法抽取6份,再从这6份试卷中随机抽取3份进行进一步分析,记 为抽取的3份试卷中测试成绩在
为抽取的3份试卷中测试成绩在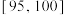 内的份数,求
内的份数,求 的分布列和数学期望.
的分布列和数学期望.参考数据:若
 ,则
,则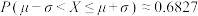 ,
,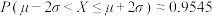 ,
,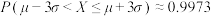 .
.
您最近一年使用:0次
2022-11-03更新
|
1217次组卷
|
7卷引用:江苏省南京师范大学附属中学2022-2023学年高三上学期期中数学试题
江苏省南京师范大学附属中学2022-2023学年高三上学期期中数学试题(已下线)第02讲 概率(练)江西省宜春中学、高安中学、上高二中、萍乡中学2023届高三11月份第一次优生联考数学(理)试题江苏省镇江市扬中市第二高级中学2022-2023学年高三上学期期末模拟数学试题(已下线)7.5 正态分布(分层作业)河南省漯河市2022-2023学年高二下学期期末数学试题(已下线)模块三 专题6 概率--(基础夯实练)(苏教版高二)
名校
解题方法
8 . 根据历史资料显示,某种慢性疾病患者的自然痊愈率为5%.为试验种新药,在有关部门批准后,医院将此药给10位病人服用,试验方案为:若这10人中至少有2人痊愈,则认为该药有效,提高了治愈率;否则,则认为该药无效.
(1)如果在该次试验中有5人痊愈,院方欲从参加该次试验的10人中随机选2人了解服药期间的感受,记抽到痊愈的人的个数为 ,求
,求 的概率分布及数学期望;
的概率分布及数学期望;
(2)如果新药有效,将治愈率提高到了50%,求通过试验却认定新药无效的概率 ,并根据
,并根据 的值解释该试验方案的合理性.
的值解释该试验方案的合理性.
(参考结论:通常认为发生概率小于5%的事件可视为小概率事件)
(1)如果在该次试验中有5人痊愈,院方欲从参加该次试验的10人中随机选2人了解服药期间的感受,记抽到痊愈的人的个数为
 ,求
,求 的概率分布及数学期望;
的概率分布及数学期望;(2)如果新药有效,将治愈率提高到了50%,求通过试验却认定新药无效的概率
 ,并根据
,并根据 的值解释该试验方案的合理性.
的值解释该试验方案的合理性.(参考结论:通常认为发生概率小于5%的事件可视为小概率事件)
您最近一年使用:0次
2020-11-30更新
|
1478次组卷
|
14卷引用:江苏省南京市第一中学2020-2021学年高三上学期期中数学试题
江苏省南京市第一中学2020-2021学年高三上学期期中数学试题江苏省南通市海安县2020-2021学年高三上学期期中调研考试数学试题江苏省南京市金陵中学、南通市海安中学2020-2021学年高三上学期期中数学试题(已下线)期末模拟试卷(B能力卷)-2020-2021学年高二数学课时同步练(人教B版2019选择性必修第二册)(已下线)4.2.4随机变量的数字特征(1)B提高练江苏省南通市海安高级中学2020-2021学年高三上学期期中数学试题(已下线)第四章 概率与统计 4.2 随机变量 4.2.4 随机变量的数字特征人教A版(2019) 选修第三册 实战演练 第七章 7.4 课时练习14 超几何分布山西省英才学校高中部2023届高三上学期12月第三次测试数学试题山东省德州市陵城区第一中学2022-2023学年高二上学期期末数学试题北京市房山区2022-2023学年高二下学期期中学业水平调研数学试题(已下线)模块二 专题3 概率与统计中决策问题湖北省部分县市区省级示范高中温德克英协作体2023-2024学年高二上学期期末综合性调研考试数学试题四川省自贡市第一中学校2023-2024学年高二下学期6月月考数学试题
名校
9 . 某学校为提高学生身体素质,号召全校学生参加体育锻炼,结合每日统计的运动情况,对每日平均运动10000步或以上的学生授予“运动达人”称号,低于10000步称为“参与者”,统计了200名学生在某月的运动数据,结果如下:
(1)完善 列联表并说明:是否有
列联表并说明:是否有 的把握认为获得“运动达人”称号与性别有关?
的把握认为获得“运动达人”称号与性别有关?
(2)从全校“运动达人”中按性别分层抽取8人,再从8人中选取3人参加特训,将特训的人中男生人数记为 ,求
,求 的分布列与均值
的分布列与均值 .
.
参考公式: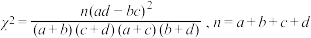
运动达人 | 参与者 | 合计 | |
男生 | 70 | ||
女生 | 80 | ||
合计 | 80 | 200 |
 列联表并说明:是否有
列联表并说明:是否有 的把握认为获得“运动达人”称号与性别有关?
的把握认为获得“运动达人”称号与性别有关?(2)从全校“运动达人”中按性别分层抽取8人,再从8人中选取3人参加特训,将特训的人中男生人数记为
 ,求
,求 的分布列与均值
的分布列与均值 .
.参考公式:
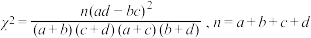
|
|
|
|
|
|
|
|
|
|
|
|
| 10.828 |
您最近一年使用:0次