名校
1 . 为深入推进传统制造业改造提升,依靠创新引领产业升级,某设备生产企业对现有生产设备进行技术攻坚突破.设备生产的零件的直径为X(单位:nm).
(1)现有旧设备生产的零件有10个,其中直径大于10nm的有2个.现从这10个零件中随机抽取3个.记 表示取出的零件中直径大于10nm的零件的个数,求
表示取出的零件中直径大于10nm的零件的个数,求 的分布列及数学期望
的分布列及数学期望 ;
;
(2)技术攻坚突破后设备生产的零件的合格率为 ,每个零件是否合格相互独立.现任取4个零件进行检测,若合格的零件数
,每个零件是否合格相互独立.现任取4个零件进行检测,若合格的零件数 超过半数,则可认为技术攻坚成功.求技术攻坚成功的概率及
超过半数,则可认为技术攻坚成功.求技术攻坚成功的概率及 的方差;
的方差;
(3)若技术攻坚后新设备生产的零件直径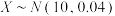 ,从生产的零件中随机取出10个,求至少有一个零件直径大于10.4nm的概率.
,从生产的零件中随机取出10个,求至少有一个零件直径大于10.4nm的概率.
参考数据:若 ,则
,则 ,
,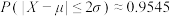 ,
,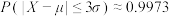 ,
,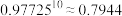 ,
,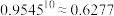 .
.
(1)现有旧设备生产的零件有10个,其中直径大于10nm的有2个.现从这10个零件中随机抽取3个.记
 表示取出的零件中直径大于10nm的零件的个数,求
表示取出的零件中直径大于10nm的零件的个数,求 的分布列及数学期望
的分布列及数学期望 ;
;(2)技术攻坚突破后设备生产的零件的合格率为
 ,每个零件是否合格相互独立.现任取4个零件进行检测,若合格的零件数
,每个零件是否合格相互独立.现任取4个零件进行检测,若合格的零件数 超过半数,则可认为技术攻坚成功.求技术攻坚成功的概率及
超过半数,则可认为技术攻坚成功.求技术攻坚成功的概率及 的方差;
的方差;(3)若技术攻坚后新设备生产的零件直径
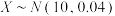 ,从生产的零件中随机取出10个,求至少有一个零件直径大于10.4nm的概率.
,从生产的零件中随机取出10个,求至少有一个零件直径大于10.4nm的概率.参考数据:若
 ,则
,则 ,
,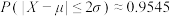 ,
,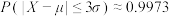 ,
,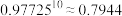 ,
,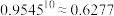 .
.
您最近一年使用:0次
2024-05-12更新
|
948次组卷
|
6卷引用:江苏省泰州中学2023-2024学年高二下学期期中考试数学试题
2 . 下列关于随机变量X的说法正确的是( )
A.若X服从正态分布 ,则 ,则 |
B.已知随机变量X服从二项分布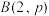 ,且 ,且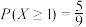 ,随机变量Y服从正态分布 ,随机变量Y服从正态分布 ,若 ,若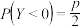 ,则 ,则 |
C.若X服从超几何分布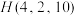 ,则期望 ,则期望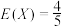 |
D.若X服从二项分布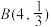 ,则方差 ,则方差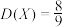 |
您最近一年使用:0次
2023-09-17更新
|
688次组卷
|
5卷引用:江苏省泰州中学2023-2024学年高三上学期第一次月度检测数学试题
江苏省泰州中学2023-2024学年高三上学期第一次月度检测数学试题江苏省郑梁梅高级中学2022-2023学年高二下学期期中数学试题(已下线)人教B版2019选择性必修第二册综合测试-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第二册)山东省潍坊市昌邑市第一中学2023-2024学年高二下学期3月月考数学试题(已下线)专题04 随机变量及其分布类常考题型归类--高二期末考点大串讲(人教B版2019选择性必修第二册)
名校
解题方法
3 . 已知某校篮球队共有9名队员,其中5名主力队员,4名替补队员.在某次训练中,该校篮球队教练从中随机地挑选3名队员进行投篮训练,每名队员至多投篮5次,一旦连续命中2次或者投完5次,都停止投篮.
(1)记选出的3名队员中主力队员的人数为随机变量 ,求
,求 的概率分布和数学期望;
的概率分布和数学期望;
(2)已知队员甲被选中参加投篮训练,假定队员甲每次投篮命中率均为 ,记队员甲投篮次数为随机变量
,记队员甲投篮次数为随机变量 ,求
,求 的概率分布和数学期望.
的概率分布和数学期望.
(1)记选出的3名队员中主力队员的人数为随机变量
 ,求
,求 的概率分布和数学期望;
的概率分布和数学期望;(2)已知队员甲被选中参加投篮训练,假定队员甲每次投篮命中率均为
 ,记队员甲投篮次数为随机变量
,记队员甲投篮次数为随机变量 ,求
,求 的概率分布和数学期望.
的概率分布和数学期望.
您最近一年使用:0次
名校
解题方法
4 . 袋中有6个大小相同的球,其中4个黑球,2个白球,现从中任取3个球,记随机变量 为其中白球的个数,随机变量
为其中白球的个数,随机变量 为其中黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量
为其中黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量 为取出3个球的总得分,则下列结论正确的是( )
为取出3个球的总得分,则下列结论正确的是( )
 为其中白球的个数,随机变量
为其中白球的个数,随机变量 为其中黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量
为其中黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量 为取出3个球的总得分,则下列结论正确的是( )
为取出3个球的总得分,则下列结论正确的是( )A. | B. |
C. | D. |
您最近一年使用:0次
解题方法
5 . 下列命题正确的是( )
A.若随机变量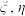 满足 满足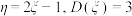 ,则 ,则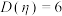 |
B.若 ,则 ,则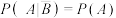 |
C.若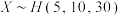 ,则 ,则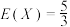 |
D.若 分布, 分布,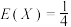 ,则 ,则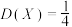 |
您最近一年使用:0次
解题方法
6 . 已知20条试题中有8条选择题,甲无放回地依次从中抽取5条题,乙有放回地依次从中抽取5条题,甲、乙每次均抽取一条试题,抽出的5条题中选择题的条数分别为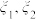 ,
,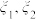 的期望分别为
的期望分别为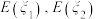 ,方差分别为
,方差分别为 ,则( )
,则( )
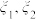 ,
,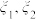 的期望分别为
的期望分别为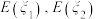 ,方差分别为
,方差分别为 ,则( )
,则( )A.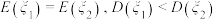 | B.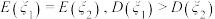 |
C.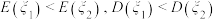 | D.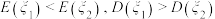 |
您最近一年使用:0次
7 . 现有10件产品,其中6件一等品,4件二等品,从中随机选出3件产品,其中一等品的件数记为随机变量X,则X的数学期望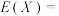
___________ .
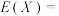
您最近一年使用:0次
2017-07-01更新
|
1246次组卷
|
5卷引用:【校级联考】江苏省兴化市第一中学2017-2018学年第二学期高二月考试卷(理科)数学



