名校
1 . 某数学兴趣小组为研究本校学生数学成绩与语文成绩的关系,采取有放回的简单随机抽样,从学校抽取样本容量为200的样本,将所得数学成绩与语文成绩的样本观测数据整理如下:
(1)根据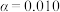 的独立性检验,能否认为数学成绩与语文成绩有关联?
的独立性检验,能否认为数学成绩与语文成绩有关联?
(2)在人工智能中常用 表示在事件
表示在事件 发生的条件下事件
发生的条件下事件 发生的优势,在统计中称为似然比.现从该校学生中任选一人,
发生的优势,在统计中称为似然比.现从该校学生中任选一人, 表示“选到的学生语文成绩不优秀”,
表示“选到的学生语文成绩不优秀”, 表示“选到的学生数学成绩不优秀”请利用样本数据,估计
表示“选到的学生数学成绩不优秀”请利用样本数据,估计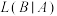 的值.
的值.
(3)现从数学成绩优秀的样本中,按分层抽样的方法选出8人组成一个小组,从抽取的8人里再随机抽取3人参加数学竞赛,求这3人中,语文成绩优秀的人数 的概率分布列及数学期望.
的概率分布列及数学期望.
附:
语文成绩 | 合计 | |||
优秀 | 不优秀 | |||
数学 成绩 | 优秀 | 50 | 30 | 80 |
不优秀 | 40 | 80 | 120 | |
合计 | 90 | 110 | 200 | |
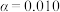 的独立性检验,能否认为数学成绩与语文成绩有关联?
的独立性检验,能否认为数学成绩与语文成绩有关联?(2)在人工智能中常用
 表示在事件
表示在事件 发生的条件下事件
发生的条件下事件 发生的优势,在统计中称为似然比.现从该校学生中任选一人,
发生的优势,在统计中称为似然比.现从该校学生中任选一人, 表示“选到的学生语文成绩不优秀”,
表示“选到的学生语文成绩不优秀”, 表示“选到的学生数学成绩不优秀”请利用样本数据,估计
表示“选到的学生数学成绩不优秀”请利用样本数据,估计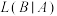 的值.
的值.(3)现从数学成绩优秀的样本中,按分层抽样的方法选出8人组成一个小组,从抽取的8人里再随机抽取3人参加数学竞赛,求这3人中,语文成绩优秀的人数
 的概率分布列及数学期望.
的概率分布列及数学期望.附:

 | 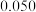 |  |  |
 |  |  |  |
您最近一年使用:0次
2023-02-17更新
|
4881次组卷
|
21卷引用:江苏省无锡市锡东高级中学2023-2024学年高二下学期5月月考数学试题
江苏省无锡市锡东高级中学2023-2024学年高二下学期5月月考数学试题湖北省荆荆宜仙四市2023届高三下学期2月联考数学试题广东省江门市第一中学2023届高三下学期2月月考数学试题安徽省滁州市定远县育才学校2023届高三下学期第一次模拟数学试题湖南省长沙市雅礼中学2023届高三下学期月考(八)数学试题湖北省随州市第一中学、荆州市龙泉中学2023届高三下学期四月联考数学试题山东省日照实验高级中学2023届高三模数学试题(已下线)专题18计数原理与概率统计(解答题)(已下线)模块六 专题2 易错题目重组卷(山东卷)专题24计数原理与概率与统计(解答题)(已下线)押新高考第19题 概率统计湖北省武汉中学2022-2023学年高二下学期5月月考数学试题广东省汕头市2022-2023学年高二下学期期末数学试题黑龙江省哈尔滨市哈尔滨德强高级中学2022-2023学年高二下学期期中数学试题宁夏回族自治区银川市唐徕中学2022-2023学年高二下学期期中考试数学(理)试题广东省东莞实验中学2022-2023学年高二下学期月考二数学试题(已下线)模块三 专题7 大题分类练(概率)基础夯实练 (已下线)专题17 概率-2重庆市永川区北山中学2024届高三上学期期中数学试题上海市向明中学2024届高三下学期三模测试数学试卷山西省太原市成成中学校2025届高三上学期9月月考数学试卷
名校
解题方法
2 . 为深入学习贯彻党的二十大精神,推动全市党员干部群众用好“学习强国”学习平台,激发干事创业热情.某单位组织“学习强国”知识竞赛,竞赛共有 道题目,随机抽取
道题目,随机抽取 道让参赛者回答.已知小明只能答对其中的
道让参赛者回答.已知小明只能答对其中的 道,试求:
道,试求:
(1)抽到他能答对题目数 的分布列;
的分布列;
(2)求 的期望和方差
的期望和方差
 道题目,随机抽取
道题目,随机抽取 道让参赛者回答.已知小明只能答对其中的
道让参赛者回答.已知小明只能答对其中的 道,试求:
道,试求:(1)抽到他能答对题目数
 的分布列;
的分布列;(2)求
 的期望和方差
的期望和方差
您最近一年使用:0次
2024-03-19更新
|
2681次组卷
|
10卷引用:第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)8.2 离散型随机变量及其分布列(3)江苏省无锡市运河实验学校2023-2024学年高二下学期期中考试数学试卷江苏高二专题08概率与统计(第二部分)上海市位育中学2023-2024学年高二下学期3月月考数学试卷河北省沧州市吴桥县吴桥中学2023-2024学年高二下学期3月月考数学试题(已下线)第七章:随机变量及其分布章末重点题型复习(7题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题07概率初步(续)全章复习攻略--高二期末考点大串讲(沪教版2020选修)浙江省学军中学紫金港校区2023-2024学年高二下学期期中数学试题(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点1 重要的概率分布模型(一)【基础版】
名校
3 . 在某校举办“青春献礼二十大,强国有我新征程”的知识能力测评中,随机抽查了100名学生,其中共有4名女生和3名男生的成绩在90分以上,从这7名同学中每次随机抽1人在全校作经验分享,每位同学最多分享一次,记第一次抽到女生为事件A,第二次抽到男生为事件B.
(1)求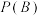 ,
, ,
,
(2)若把抽取学生的方式更改为:从这7名学生中随机抽取3人进行经验分享,记被抽取的3人中女生的人数为X,求X的分布列和数学期望.
(1)求
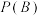 ,
, ,
,(2)若把抽取学生的方式更改为:从这7名学生中随机抽取3人进行经验分享,记被抽取的3人中女生的人数为X,求X的分布列和数学期望.
您最近一年使用:0次
2023-02-15更新
|
2597次组卷
|
13卷引用:8.2.3-8.2.4二项分布 超几何分布(练习)
(已下线)8.2.3-8.2.4二项分布 超几何分布(练习)(已下线)第8章 概率 单元综合检测(练习)云南省红河州2023届高三第一次复习统一检测(一模)数学试题(已下线)模块十 计数原理与统计概率-1(已下线)7.4 二项分布与超几何分布(练习)(已下线)专题18计数原理与概率统计(解答题)黑龙江省大庆市大庆实验中学2022-2023学年高二下学期4月月考数学试题(已下线)随机变量及其分布章末检测卷(一)-【帮课堂】2022-2023学年高二数学同步精品讲义(人教A版2019选择性必修第三册)(已下线)第6章 计数原理(A卷·知识通关练)(3)(已下线)第7章 概率初步(续)(A卷·知识通关练)(2)吉林省“BEST合作体”2022-2023学年高二下学期期末联考数学试题黑龙江省鸡西市鸡冠区鸡西实验中学2022-2023学年高二下学期期末数学试题湖北省荆州市松滋市第一中学2024届高三上学期12月月考模拟数学试题(二)
名校
解题方法
4 . 2024年“与辉同行”直播间开播,董宇辉领衔7位主播从“心”出发,其中男性5人,女性3人,现需排班晚8:00黄金档,随机抽取两人,则男生人数的期望为( )
A. | B. | C.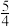 | D.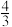 |
您最近一年使用:0次
2024-03-31更新
|
1436次组卷
|
8卷引用:专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)
(已下线)专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)(已下线)专题06 离散型随机变量分布列及正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)吉林省长春市东北师范大学附属中学2023-2024学年高二下学期3月月考数学试题(已下线)7.4 二项分布与超几何分布(8大题型)精讲-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)安徽省六安市六安第一中学2024届高考模拟预测数学试题(四)江西省宜春市宜丰中学创新部2023-2024学年高一下学期6月月考数学试题(已下线)专题04 随机变量的均值与方差综合--高二期末考点大串讲(人教B版2019选择性必修第二册)四川省自贡市第一中学校2023-2024学年高二下学期6月月考数学试题
5 . 袋中有10个大小相同的球,其中6个黑球,4个白球,现从中任取4个球,记随机变量X为其中白球的个数,随机变量Y为其中黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量Z为取出4个球的总得分,则下列结论中正确的是( )
A.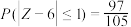 | B. |
C. | D.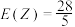 |
您最近一年使用:0次
2022-05-31更新
|
2688次组卷
|
9卷引用:江苏省南京师范大学附属中学2021-2022学年高二下学期期末模拟数学试题
江苏省南京师范大学附属中学2021-2022学年高二下学期期末模拟数学试题江苏省南通市海安高级中学2024届高三上学期1月学情调研数学试题湖北省华中师大一附中2022届高三下学期高考前测试数学试题(已下线)专题34 随机变量及其分布列(针对训练)-2023年高考一轮复习精讲精练宝典(新高考专用)(已下线)7.4.2 超几何分布 (精练)(已下线)专题20 概率与统计常考小题归类(15大题型)(练习)(已下线)第07讲 7.4.2超几何分布-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)7.4.2 超几何分布——课后作业(提升版)新疆兵团第三师图木舒克市鸿德实验学校2023-2024学年高二下学期第二次月考数学试卷
名校
解题方法
6 . 学校师生参与创城志愿活动.高二(1)班某小组有男生4人,女生2人,现从中随机选取2人作为志愿者参加活动.
(1)求在有女生参加活动的条件下,恰有一名女生参加活动的概率;
(2)记参加活动的女生人数为 ,求
,求 的分布列及期望
的分布列及期望 ;
;
(3)若志愿活动共有卫生清洁员、交通文明监督员、科普宣传员三项可供选择.每名女生至多从中选择2项活动,且选择参加1项或2项的可能性均为 ;每名男生至少从中选择参加2项活动,且选择参加2项或3项的可能性也均为
;每名男生至少从中选择参加2项活动,且选择参加2项或3项的可能性也均为 .每人每参加1项活动可获得3个工时,记随机选取的两人所得工时之和为
.每人每参加1项活动可获得3个工时,记随机选取的两人所得工时之和为 ,求
,求 的期望
的期望 .
.
(1)求在有女生参加活动的条件下,恰有一名女生参加活动的概率;
(2)记参加活动的女生人数为
 ,求
,求 的分布列及期望
的分布列及期望 ;
;(3)若志愿活动共有卫生清洁员、交通文明监督员、科普宣传员三项可供选择.每名女生至多从中选择2项活动,且选择参加1项或2项的可能性均为
 ;每名男生至少从中选择参加2项活动,且选择参加2项或3项的可能性也均为
;每名男生至少从中选择参加2项活动,且选择参加2项或3项的可能性也均为 .每人每参加1项活动可获得3个工时,记随机选取的两人所得工时之和为
.每人每参加1项活动可获得3个工时,记随机选取的两人所得工时之和为 ,求
,求 的期望
的期望 .
.
您最近一年使用:0次
2024-05-08更新
|
914次组卷
|
6卷引用:江苏省镇江市八校2023~2024学年高二下学期期末联考数学试卷
江苏省镇江市八校2023~2024学年高二下学期期末联考数学试卷福建省宁化第一中学2023-2024学年高二下学期第一次阶段考试数学试题(已下线)第七章:随机变量及其分布章末综合检测卷(新题型)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)广东省揭阳市惠来县第一中学2023-2024学年高二下学期6月月考数学试题江西省鹰潭市2023-2024学年高二下学期期末质量检测数学试卷广东省湛江市2023-2024学年高二下学期期末调研考试数学试卷
名校
7 . 已知某地区秋季的昼夜温差 ,且
,且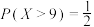 ,该地区某班级秋季每天感冒的人数y关于昼夜温差
,该地区某班级秋季每天感冒的人数y关于昼夜温差 的经验回归方程为
的经验回归方程为 ,秋季某天该班级感冒的学生有9人,其中有4位男生,5位女生,则下列结论正确的是( )
,秋季某天该班级感冒的学生有9人,其中有4位男生,5位女生,则下列结论正确的是( )
(参考数据: ,
, )
)
 ,且
,且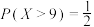 ,该地区某班级秋季每天感冒的人数y关于昼夜温差
,该地区某班级秋季每天感冒的人数y关于昼夜温差 的经验回归方程为
的经验回归方程为 ,秋季某天该班级感冒的学生有9人,其中有4位男生,5位女生,则下列结论正确的是( )
,秋季某天该班级感冒的学生有9人,其中有4位男生,5位女生,则下列结论正确的是( )(参考数据:
 ,
, )
)A.若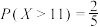 ,则 ,则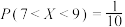 |
B.从这9人中随机抽取2人,其中至少有一位女生的概率为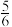 |
C.从这9人中随机抽取2人,其中男生人数 的期望为 的期望为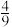 |
D.昼夜温差每提高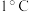 ,该班级感冒的学生大约增加2人 ,该班级感冒的学生大约增加2人 |
您最近一年使用:0次
2023-10-07更新
|
522次组卷
|
5卷引用:江苏省2024届高三上学期期末迎考数学试题
江苏省2024届高三上学期期末迎考数学试题皖豫名校联盟2024届高三第一次考试数学试题皖豫名校联盟2024届高中毕业班高三上学期10月大联考数学试题(已下线)第九章 重难专攻(十二)概率中的综合题 A素养养成卷 一轮点点通安徽省合肥市巢湖市第一中学2024届高三上学期10月月考数学试题
名校
8 . 某车企随机调查了今年某月份购买本车企生产的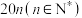 台新能源汽车车主,统计得到以下
台新能源汽车车主,统计得到以下 列联表,经过计算可得
列联表,经过计算可得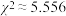 .
.
(1)完成表格并求出 值,并判断有多大的把握认为购车消费者对新能源车的喜欢情况与性别有关;
值,并判断有多大的把握认为购车消费者对新能源车的喜欢情况与性别有关;
(2)采用比例分配的分层抽样法从调查的不喜欢和喜欢新能源汽车的车主中随机抽取12人,再从抽取的12人中抽取4人,设被抽取的4人中属于不喜欢新能源汽车的人数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
附: ,其中
,其中 .
.
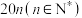 台新能源汽车车主,统计得到以下
台新能源汽车车主,统计得到以下 列联表,经过计算可得
列联表,经过计算可得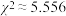 .
.| 喜欢 | 不喜欢 | 总计 | |
| 男性 |  | 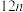 | |
| 女性 |  | ||
| 总计 |  |
 值,并判断有多大的把握认为购车消费者对新能源车的喜欢情况与性别有关;
值,并判断有多大的把握认为购车消费者对新能源车的喜欢情况与性别有关;(2)采用比例分配的分层抽样法从调查的不喜欢和喜欢新能源汽车的车主中随机抽取12人,再从抽取的12人中抽取4人,设被抽取的4人中属于不喜欢新能源汽车的人数为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望.附:
 ,其中
,其中 .
. | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2023-07-06更新
|
428次组卷
|
3卷引用:【江苏专用】高二下学期期末模拟测试A卷
(已下线)【江苏专用】高二下学期期末模拟测试A卷湖北省武汉市部分重点中学2022-2023学年高二下学期期末联考数学试题广东省肇庆市肇庆鼎湖中学2023-2024学年高二下学期期末统考模拟测试(6月月考)数学试题
名校
解题方法
9 . 某社区为了推动全民健身,增加人们对体育运动的兴趣,随机抽取了男,女各 200 人做 统计调查. 统计显示,被调查的人中,喜欢运动的男性有 100 人,不喜欢运动的女性有 50 人.
(1)完成下面列联表,并判断能否在犯错误概率不超过 0.005的情况下认为人们喜欢运动与性别有关;
(2)为了鼓励全民运动,社区开展一次趣味体育比赛,并设置3个奖项,每个奖项有且仅有 一人获取,每人最多只能获得 1 个奖项; 现从这 400 人中选出男性4人,女性4人参加 比赛,记 为获奖的男性人数,求
为获奖的男性人数,求 的分布列和数学期望.
的分布列和数学期望.
附:
(1)完成下面列联表,并判断能否在犯错误概率不超过 0.005的情况下认为人们喜欢运动与性别有关;
喜欢 | 不喜欢 | 合计 | |
男性 | |||
女性 | |||
合计 |
 为获奖的男性人数,求
为获奖的男性人数,求 的分布列和数学期望.
的分布列和数学期望.附:

| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-05-27更新
|
416次组卷
|
2卷引用:江苏省如皋中学2023-2024学年高二下学期教学质量调研(二)数学试题



