名校
解题方法
1 . 锚定2060碳中和,中国能源演进“绿之道”,为响应绿色低碳发展的号召,某地在沙漠治理过程中,计划在沙漠试点区域四周种植红柳和梭梭树用于防风固沙,中间种植适合当地环境的特色经济作物,通过大量实验发现,单株经济作物幼苗的成活率为0.8,红柳幼苗和梭梭树幼苗成活的概率均为p,且已知任取三种幼苗各一株,其中至少有两株幼苗成活的概率不超过0.896.
(1)当p最大时,经济作物幼苗的成活率也将提升至0.88,求此时三种幼苗均成活的概率(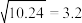 );
);
(2)正常情况下梭梭树幼苗栽种5年后,其树杆地径服从正态分布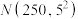 (单位:mm).
(单位:mm).
㈠梭梭树幼苗栽种5年后,若任意抽取一棵梭梭树,则树杆地径小于235mm的概率约为多少?(精确到0.001)
㈡为更好地监管梭梭树的生长情况,梭梭树幼苗栽种5年后,农林管理员随机抽取了10棵梭梭树,测得其树杆地径均小于235mm,农林管理员根据抽检结果,认为该地块土质对梭梭树的生长产生影响,计划整改地块并选择合适的肥料,试判断该农林管理员的判断是否合理?并说明理由.
附:若随机变量Z服从正态分布 ,则
,则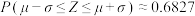 ,
,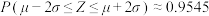 ,
,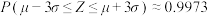 .
.
(1)当p最大时,经济作物幼苗的成活率也将提升至0.88,求此时三种幼苗均成活的概率(
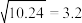 );
);(2)正常情况下梭梭树幼苗栽种5年后,其树杆地径服从正态分布
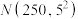 (单位:mm).
(单位:mm).㈠梭梭树幼苗栽种5年后,若任意抽取一棵梭梭树,则树杆地径小于235mm的概率约为多少?(精确到0.001)
㈡为更好地监管梭梭树的生长情况,梭梭树幼苗栽种5年后,农林管理员随机抽取了10棵梭梭树,测得其树杆地径均小于235mm,农林管理员根据抽检结果,认为该地块土质对梭梭树的生长产生影响,计划整改地块并选择合适的肥料,试判断该农林管理员的判断是否合理?并说明理由.
附:若随机变量Z服从正态分布
 ,则
,则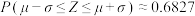 ,
,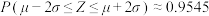 ,
,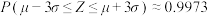 .
.
您最近一年使用:0次
2023-04-27更新
|
1674次组卷
|
5卷引用:辽宁省锦州市渤海大学附属高级中学2023届高三第六次模拟考试数学试题
辽宁省锦州市渤海大学附属高级中学2023届高三第六次模拟考试数学试题四川省名校联盟2023届高三下学期4月联考理科数学试题 重庆市巴蜀中学校2023届高三下学期4月月考数学试题广东省深圳市高级中学(集团)2023届高三适应性考数学试题(已下线)3.3 正态分布(同步练习)-【素养提升—课时练】2022-2023学年高二数学湘教版选择性必修第二册检测 (提高篇)
名校
解题方法
2 . 据相关机构调查表明我国中小学生身体健康状况不容忽视,多项身体指标(如肺活量、柔㓞度、力量、速度、耐力等)自2000年起呈下降趋势,并且下降趋势明显,在国家的积极干预下,这种状况得到遏制,并向好的方向发展,到2019年中小学生在肺活量、柔㓞度、力量、速度、而力等多项指标出现好转,但肥胖、近视等问题依然严重,体育事业任重道远.某初中学校为提高学生身体素质,日常组织学生参加中短跑锻炼,学校在一次百米短跑测试中,抽取200名女生作为样本,统计她们的成绩(单位:秒),整理得到如图所示的频率分布直方图(每组区间包含左端点,不包含右端点).
(2)由频率分布直方图,可以认为该校女生的短跑成绩 ,其中
,其中 近似为女生短跑平均成绩
近似为女生短跑平均成绩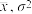 近似为样本方差
近似为样本方差 ,经计算得
,经计算得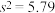 ,若从该校女生中随机抽取10人,记其中短跑成绩在
,若从该校女生中随机抽取10人,记其中短跑成绩在 内的人数为
内的人数为 ,求
,求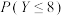 (结果保留2个有效数字).
(结果保留2个有效数字).
附参考数据: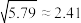 ,随机变量
,随机变量 服从正态分布
服从正态分布 ,则
,则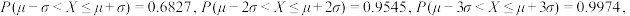
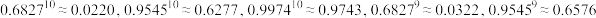 .
.
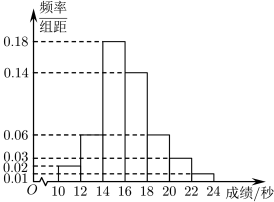
(2)由频率分布直方图,可以认为该校女生的短跑成绩
 ,其中
,其中 近似为女生短跑平均成绩
近似为女生短跑平均成绩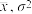 近似为样本方差
近似为样本方差 ,经计算得
,经计算得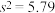 ,若从该校女生中随机抽取10人,记其中短跑成绩在
,若从该校女生中随机抽取10人,记其中短跑成绩在 内的人数为
内的人数为 ,求
,求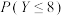 (结果保留2个有效数字).
(结果保留2个有效数字).附参考数据:
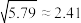 ,随机变量
,随机变量 服从正态分布
服从正态分布 ,则
,则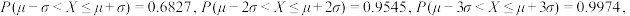
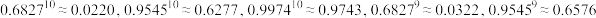 .
.
您最近一年使用:0次
2023-05-29更新
|
1213次组卷
|
6卷引用:辽宁省锦州市2023届高三质量监测数学试题(最后一模)
辽宁省锦州市2023届高三质量监测数学试题(最后一模)四川省2023届名校联考高考仿真测试(一)理科数学试题河北省沧州市沧县中学2023届高考猜题信息卷(一)数学试题(已下线)模块一 专题4 《概率和分布》单元检测篇 A基础卷(已下线)第08讲 7.5 正态分布(2)(已下线)7.5 正态分布——随堂检测
名校
3 . 某产品的尺寸与标准尺寸的误差绝对值不超过4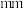 即视为合格品,否则视为不合格品.假设误差服从正态分布且每件产品是否为合格品相互独立.现随机抽取100件产品,误差的样本均值为0,样本方差为4.用样本估计总体.
即视为合格品,否则视为不合格品.假设误差服从正态分布且每件产品是否为合格品相互独立.现随机抽取100件产品,误差的样本均值为0,样本方差为4.用样本估计总体.
(1)试估计100件产品中不合格品的件数(精确到1);
(2)在(1)的条件下,现出售随机包装的100箱该产品,每箱均有100件产品.收货方对每箱产品均采取不放回地随机抽取方式进行检验,箱与箱之间的检验相互独立.每箱按以下规则判断是否接受该箱产品:如果抽检的第1件产品不合格,则拒绝该箱产品;如果抽检的第1件产品合格,则再抽1件,如果抽检的第2件产品合格,则接受该箱产品,否则拒绝该箱产品.若该箱产品通过检验后生产方获利1000元;该箱产品被拒绝,则亏损89元.求100箱该产品利润的期望值.
附:若随机变量 服从正态分布
服从正态分布 ,则
,则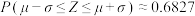 ,
,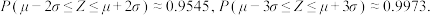
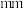 即视为合格品,否则视为不合格品.假设误差服从正态分布且每件产品是否为合格品相互独立.现随机抽取100件产品,误差的样本均值为0,样本方差为4.用样本估计总体.
即视为合格品,否则视为不合格品.假设误差服从正态分布且每件产品是否为合格品相互独立.现随机抽取100件产品,误差的样本均值为0,样本方差为4.用样本估计总体.(1)试估计100件产品中不合格品的件数(精确到1);
(2)在(1)的条件下,现出售随机包装的100箱该产品,每箱均有100件产品.收货方对每箱产品均采取不放回地随机抽取方式进行检验,箱与箱之间的检验相互独立.每箱按以下规则判断是否接受该箱产品:如果抽检的第1件产品不合格,则拒绝该箱产品;如果抽检的第1件产品合格,则再抽1件,如果抽检的第2件产品合格,则接受该箱产品,否则拒绝该箱产品.若该箱产品通过检验后生产方获利1000元;该箱产品被拒绝,则亏损89元.求100箱该产品利润的期望值.
附:若随机变量
 服从正态分布
服从正态分布 ,则
,则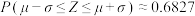 ,
,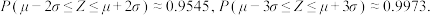
您最近一年使用:0次
2024-03-07更新
|
993次组卷
|
4卷引用:辽宁省锦州市某校2023-2024学年高三下学期考前测试数学试卷(A)
辽宁省锦州市某校2023-2024学年高三下学期考前测试数学试卷(A)安徽省江南十校2024届高三3月联考数学试卷(已下线)第七章 概率初步(续)(知识归纳+题型突破)(3)(已下线)第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
名校
解题方法
4 . 法国数学家庞加莱是个喜欢吃面包的人,他每天都会到同一家面包店购买一个面包.该面包店的面包师声称自己所出售的面包的平均质量是1 000 g,上下浮动不超过50 g.这句话用数学语言来表达就是:每个面包的质量服从期望为1 000 g,标准差为50 g的正态分布.
(1)已知如下结论:若X~N(μ,σ2),从X的取值中随机抽取k(k∈N*,k≥2)个数据,记这k个数据的平均值为Y,则随机变量Y~N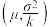 .利用该结论解决下面问题.
.利用该结论解决下面问题.
①假设面包师的说法是真实的,随机购买25个面包,记随机购买25个面包的平均值为Y,求P(Y≤980);
②庞加莱每天都会将买来的面包称重并记录,25天后,得到的数据都落在区间(950,1 050)内,并得出计算25个面包的平均质量为978.72 g.庞加莱通过分析举报了该面包师,从概率角度说明庞加莱举报该面包师的理由;
(2)假设有两箱面包(面包除颜色外,其他都一样),已知第一箱中共装有6个面包,其中黑色面包2个;第二箱中共装有8个面包,其中黑色面包3个.现随机挑选一箱,然后从该箱中随机取出2个面包,求取出黑色面包个数的分布列及数学期望.
附:①若随机变量η服从正态分布N(μ,σ2),则P(μ-σ≤η≤μ+σ)≈0.682 7,P(μ-2σ≤η≤μ+2σ)≈0.954 5,P(μ-3σ≤η≤μ+3σ)≈0.997 3;②通常把发生概率小于0.05的事件称为小概率事件,小概率事件基本不会发生.
(1)已知如下结论:若X~N(μ,σ2),从X的取值中随机抽取k(k∈N*,k≥2)个数据,记这k个数据的平均值为Y,则随机变量Y~N
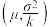 .利用该结论解决下面问题.
.利用该结论解决下面问题.①假设面包师的说法是真实的,随机购买25个面包,记随机购买25个面包的平均值为Y,求P(Y≤980);
②庞加莱每天都会将买来的面包称重并记录,25天后,得到的数据都落在区间(950,1 050)内,并得出计算25个面包的平均质量为978.72 g.庞加莱通过分析举报了该面包师,从概率角度说明庞加莱举报该面包师的理由;
(2)假设有两箱面包(面包除颜色外,其他都一样),已知第一箱中共装有6个面包,其中黑色面包2个;第二箱中共装有8个面包,其中黑色面包3个.现随机挑选一箱,然后从该箱中随机取出2个面包,求取出黑色面包个数的分布列及数学期望.
附:①若随机变量η服从正态分布N(μ,σ2),则P(μ-σ≤η≤μ+σ)≈0.682 7,P(μ-2σ≤η≤μ+2σ)≈0.954 5,P(μ-3σ≤η≤μ+3σ)≈0.997 3;②通常把发生概率小于0.05的事件称为小概率事件,小概率事件基本不会发生.
您最近一年使用:0次
2024-03-21更新
|
500次组卷
|
21卷引用:辽宁省锦州市某校2023-2024学年高三上学期第二次考试数学试题
辽宁省锦州市某校2023-2024学年高三上学期第二次考试数学试题山东省青岛市四区2021-2022学年高三上学期期末考试数学试题福建省尤溪第一中学2021~2022学年高二下学期数学期末模拟卷(三)试题湖南省长沙市雅礼中学2022-2023学年高三上学期月考(五)数学试题山东省青岛市4区县2021-2022学年高三上学期期末考试数学试题浙江省杭州第二中学2023届高三下学期3月月考数学试题江苏省常州市溧阳中学2022-2023学年高二下学期4月阶段性调研测试数学试题江苏省扬州中学2023届高三下学期阶段测试数学试题河北省保定市六校联盟2022-2023学年高二下学期4月联考数学试题江苏省盐城市伍佑中学2023届高三高考热身考试数学试题(已下线)8.3 正态分布辽宁省大连市第八中学2023届高考适应性测试数学试题福建省厦门第一中学2023届高三二模数学试题(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(讲义)-3(已下线)专题04 超几何分布+二项分布+正态分布压轴题(3)(已下线)第八章 概率(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第二册)(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第8章 概率单元综合能力测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第七章:随机变量及其分布章末重点题型复习-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)黑龙江省牡丹江市第一高级中学2023-2024学年高二下学期5月期中考试数学试题(已下线)专题06 离散型随机变量与正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)
解题方法
5 . 某城市每年6月份的平均气温t近似服从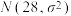 ,若
,若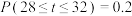 ,则可估计该城市6月份平均气温低于24摄氏度的天数为
,则可估计该城市6月份平均气温低于24摄氏度的天数为______ .
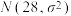 ,若
,若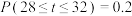 ,则可估计该城市6月份平均气温低于24摄氏度的天数为
,则可估计该城市6月份平均气温低于24摄氏度的天数为
您最近一年使用:0次



