名校
解题方法
1 . 舒腾尺是荷兰数学家舒腾(1615-1660)设计的一种作图工具,如图, 是滑槽
是滑槽 的中点,短杆
的中点,短杆 可绕
可绕 转动,长杆
转动,长杆 通过
通过 处的铰链与
处的铰链与 连接,
连接, 上的栓子
上的栓子 可沿滑槽
可沿滑槽 滑动.当点
滑动.当点 在滑槽
在滑槽 内作往复移动时,带动点
内作往复移动时,带动点 绕
绕 转动,点
转动,点 也随之而运动.记点
也随之而运动.记点 的运动轨迹为
的运动轨迹为 ,点
,点 的运动轨迹为
的运动轨迹为 .若
.若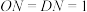 ,
,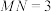 ,过
,过 上的点
上的点 向
向 作切线,则切线长的最大值为
作切线,则切线长的最大值为___________ .
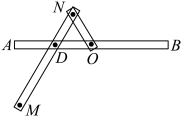
 是滑槽
是滑槽 的中点,短杆
的中点,短杆 可绕
可绕 转动,长杆
转动,长杆 通过
通过 处的铰链与
处的铰链与 连接,
连接, 上的栓子
上的栓子 可沿滑槽
可沿滑槽 滑动.当点
滑动.当点 在滑槽
在滑槽 内作往复移动时,带动点
内作往复移动时,带动点 绕
绕 转动,点
转动,点 也随之而运动.记点
也随之而运动.记点 的运动轨迹为
的运动轨迹为 ,点
,点 的运动轨迹为
的运动轨迹为 .若
.若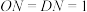 ,
,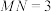 ,过
,过 上的点
上的点 向
向 作切线,则切线长的最大值为
作切线,则切线长的最大值为
您最近一年使用:0次
2023-09-10更新
|
285次组卷
|
12卷引用:江苏省南通市2021届高三下学期5月四模数学试题
江苏省南通市2021届高三下学期5月四模数学试题(已下线)第11题 与圆有关的最值问题-2021年高考数学真题逐题揭秘与以例及类(新高考全国Ⅰ卷)(已下线)2.2 直线与圆的位置关系(B 能力培优练)-2021-2022学年高二数学上学期同步双培优检测(苏教版2019选择性必修第一册)浙江省湖州市三贤联盟2021-2022学年高二上学期期中联考数学试题(已下线)第二章 圆与方程(选拔卷)-【单元测试】2021-2022学年高二数学尖子生选拔卷(苏教版2019选择性必修第一册)(已下线)专题26 求动点轨迹方程 微点7 求动点轨迹方程综合训练江苏省宿迁市沭阳县建陵高级中学2022-2023学年高三上学期期中数学试题(已下线)技巧02 填空题的答题技巧(8大题型)(练习)2023版 北师大版(2019) 选修第一册 名师精选卷 第一、二、三章滚动测试广东省大湾区2022-2023学年高二上学期期末联考数学试题(已下线)第2章 直线和圆的方程(基础、典型、新文化、压轴)分类专项训练福建省泉州市晋江学校2023-2024学年高二上学期第二次月考数学试题
2 . 已知曲线 的极坐标方程是
的极坐标方程是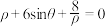 ,以极点
,以极点 为平面直角坐标系的原点,极轴为
为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,在平面直角坐标系
轴的正半轴,建立平面直角坐标系,在平面直角坐标系 中,曲线
中,曲线 .
.
(1)写出 的直角坐标方程和
的直角坐标方程和 的参数方程;
的参数方程;
(2)设 分别为
分别为 上的任意一点,求
上的任意一点,求 的最大值.
的最大值.
 的极坐标方程是
的极坐标方程是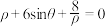 ,以极点
,以极点 为平面直角坐标系的原点,极轴为
为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,在平面直角坐标系
轴的正半轴,建立平面直角坐标系,在平面直角坐标系 中,曲线
中,曲线 .
.(1)写出
 的直角坐标方程和
的直角坐标方程和 的参数方程;
的参数方程;(2)设
 分别为
分别为 上的任意一点,求
上的任意一点,求 的最大值.
的最大值.
您最近一年使用:0次
2022高三·全国·专题练习
解题方法
3 . 已知点M是椭圆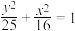 上的一动点,点T的坐标为
上的一动点,点T的坐标为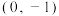 ,点N满足
,点N满足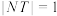 ,且
,且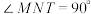 ,则
,则 的最小值是
的最小值是______ .
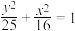 上的一动点,点T的坐标为
上的一动点,点T的坐标为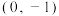 ,点N满足
,点N满足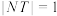 ,且
,且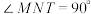 ,则
,则 的最小值是
的最小值是
您最近一年使用:0次
2022-08-29更新
|
143次组卷
|
3卷引用:四川省成都市蓉城名校联盟2021-2022学年高三上学期入学联考理科数学试题
四川省成都市蓉城名校联盟2021-2022学年高三上学期入学联考理科数学试题(已下线)第十一章 圆锥曲线专练5—椭圆小题最值问题-2022届高三数学一轮复习【课堂例】2.5.2 简单的参数方程 课堂例题 沪教版(2020)选择性必修第一册 第2章 圆锥曲线
解题方法
4 . 已知直线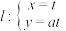
 为参数,
为参数, ,以坐标原点
,以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为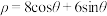 ,圆
,圆 与极轴和直线
与极轴和直线 分别交于点
分别交于点 ,点
,点 (异于坐标原点).
(异于坐标原点).
(1)写出点 的极坐标及圆
的极坐标及圆 的参数方程;
的参数方程;
(2)求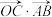 的最大值.
的最大值.
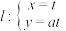
 为参数,
为参数, ,以坐标原点
,以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为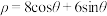 ,圆
,圆 与极轴和直线
与极轴和直线 分别交于点
分别交于点 ,点
,点 (异于坐标原点).
(异于坐标原点).(1)写出点
 的极坐标及圆
的极坐标及圆 的参数方程;
的参数方程;(2)求
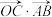 的最大值.
的最大值.
您最近一年使用:0次
2022-03-16更新
|
402次组卷
|
7卷引用:广西2021届高三综合能力测试(CAT)(一)3月联考数学(文)试题
5 . 在直角坐标系 中,直线l的参数方程为
中,直线l的参数方程为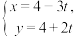 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为 .
.
(1)求直线l和曲线C的普通方程,并说明C表示什么曲线;
(2)把曲线C上所有点的纵坐标变为原来的一半,横坐标不变,得到曲线 ,B为曲线
,B为曲线 上的动点,M为
上的动点,M为 和B的中点,求M到直线l距离的最小值.
和B的中点,求M到直线l距离的最小值.
 中,直线l的参数方程为
中,直线l的参数方程为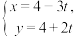 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为 .
.(1)求直线l和曲线C的普通方程,并说明C表示什么曲线;
(2)把曲线C上所有点的纵坐标变为原来的一半,横坐标不变,得到曲线
 ,B为曲线
,B为曲线 上的动点,M为
上的动点,M为 和B的中点,求M到直线l距离的最小值.
和B的中点,求M到直线l距离的最小值.
您最近一年使用:0次
2022-02-26更新
|
651次组卷
|
3卷引用:青铜鸣2021-2022学年高三上学期12月大联考数学(理科)试题
青铜鸣2021-2022学年高三上学期12月大联考数学(理科)试题青铜鸣2021-2022学年高三上学期12月大联考数学(文科)试题(已下线)解密23 坐标系与参数方程 (讲义)-【高频考点解密】2022年高考数学(理)二轮复习讲义+分层训练(全国通用)
解题方法
6 . 在直角坐标系xOy中,曲线C的参数方程为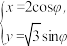 (
( 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为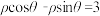 .
.
(1)求曲线C的普通方程和直线l的直角坐标方程;
(2)若点P在曲线C上,点Q在直线l上,求|PQ|的最小值.
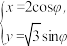 (
( 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为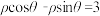 .
.(1)求曲线C的普通方程和直线l的直角坐标方程;
(2)若点P在曲线C上,点Q在直线l上,求|PQ|的最小值.
您最近一年使用:0次
2022-02-18更新
|
511次组卷
|
3卷引用:河南省六市重点高中2021-2022学年高三上学期11月联合考试数学(文)试题
河南省六市重点高中2021-2022学年高三上学期11月联合考试数学(文)试题河南省六市重点高中2021-2022学年高三上学期11月联合考试数学(理)试题(已下线)解密23 坐标系与参数方程(分层训练)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(全国通用)
名校
解题方法
7 . 在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为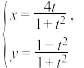 (
( 为参数).以坐标原点
为参数).以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为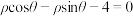
(1)求 普通方程和
普通方程和 的直角坐标方程;
的直角坐标方程;
(2)若 为曲线
为曲线 上任意一点,直线
上任意一点,直线 与
与 轴、
轴、 轴的交点分别为
轴的交点分别为 ,求
,求 面积的最大值.
面积的最大值.
 中,曲线
中,曲线 的参数方程为
的参数方程为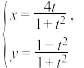 (
( 为参数).以坐标原点
为参数).以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为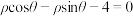
(1)求
 普通方程和
普通方程和 的直角坐标方程;
的直角坐标方程;(2)若
 为曲线
为曲线 上任意一点,直线
上任意一点,直线 与
与 轴、
轴、 轴的交点分别为
轴的交点分别为 ,求
,求 面积的最大值.
面积的最大值.
您最近一年使用:0次
2022-01-03更新
|
2278次组卷
|
5卷引用:河南省2021-2022学年高三上学期第五次联考理科数学试题
8 . 在平面直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数).以坐标原点
为参数).以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为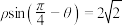 .
.
(1)求曲线 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;
(2)根据变换公式 ,由曲线
,由曲线 变换得到曲线
变换得到曲线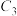 ,设点
,设点 是曲线
是曲线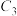 上的一个动点,设曲线
上的一个动点,设曲线 和
和 相交于
相交于 、
、 两点,求
两点,求 的面积的最大值.
的面积的最大值.
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数).以坐标原点
为参数).以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为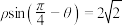 .
.(1)求曲线
 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;(2)根据变换公式
 ,由曲线
,由曲线 变换得到曲线
变换得到曲线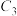 ,设点
,设点 是曲线
是曲线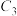 上的一个动点,设曲线
上的一个动点,设曲线 和
和 相交于
相交于 、
、 两点,求
两点,求 的面积的最大值.
的面积的最大值.
您最近一年使用:0次
名校
9 . 在直角坐标系 中,以坐标原点为极点,
中,以坐标原点为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.
(1)将 的极坐标方程化为直角坐标方程和参数方程;
的极坐标方程化为直角坐标方程和参数方程;
(2)设点 的直角坐标为
的直角坐标为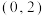 ,
, 为
为 上的动点,点
上的动点,点 满足
满足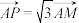 ,写出
,写出 的轨迹
的轨迹 的参数方程,并判断
的参数方程,并判断 与
与 是否有公共点.
是否有公共点.
 中,以坐标原点为极点,
中,以坐标原点为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)将
 的极坐标方程化为直角坐标方程和参数方程;
的极坐标方程化为直角坐标方程和参数方程;(2)设点
 的直角坐标为
的直角坐标为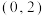 ,
, 为
为 上的动点,点
上的动点,点 满足
满足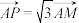 ,写出
,写出 的轨迹
的轨迹 的参数方程,并判断
的参数方程,并判断 与
与 是否有公共点.
是否有公共点.
您最近一年使用:0次
2021-12-15更新
|
866次组卷
|
3卷引用:新疆喀什第六中学2022届高三12月月考数学试题
10 . 在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为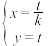 (
( 为参数),直线
为参数),直线 的参数方程为
的参数方程为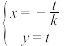 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.
(1)求曲线 的一个参数方程;
的一个参数方程;
(2)若 与
与 交于
交于 ,
, 两点,
两点, 与
与 交于
交于 ,
, 两点,求四边形
两点,求四边形 周长的最大值.
周长的最大值.
 中,直线
中,直线 的参数方程为
的参数方程为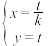 (
( 为参数),直线
为参数),直线 的参数方程为
的参数方程为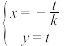 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 的一个参数方程;
的一个参数方程;(2)若
 与
与 交于
交于 ,
, 两点,
两点, 与
与 交于
交于 ,
, 两点,求四边形
两点,求四边形 周长的最大值.
周长的最大值.
您最近一年使用:0次
2021-12-14更新
|
895次组卷
|
5卷引用:河南省新乡县第一中学2021-2022学年高三上学期高考适应性测试卷(二)文数试题
河南省新乡县第一中学2021-2022学年高三上学期高考适应性测试卷(二)文数试题(已下线)专题28 极坐标与参数方程解答题20题-备战2022年高考数学冲刺横向强化精练精讲河南省洛阳市新安县第一高级中学2022届高三高考考前模拟数学理科试题河南省新乡市第一中学2023届高三三轮冲刺能力测试第六测理科数学试题河南省2022届高三上学期期末模拟数学(理)试题(六)



