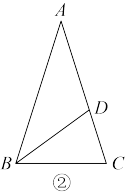
如图, 内接于圆O,连接
内接于圆O,连接 .
.
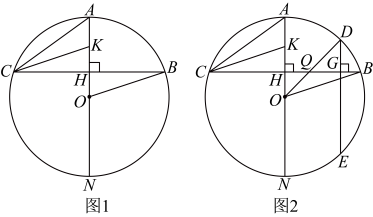
(1)如图1,求证: ;
;
(2)如图2, 于D交圆O于E,
于D交圆O于E, 于H,求证:
于H,求证: ;
;
(3)如图3,在(2)的条件下,若 平分
平分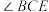 ,延长
,延长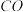 交
交 于P,
于P, ,
,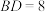 ,求
,求 长.
长.
 内接于圆O,连接
内接于圆O,连接 .
.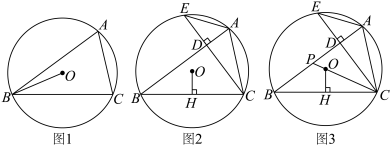
(1)如图1,求证:
 ;
;(2)如图2,
 于D交圆O于E,
于D交圆O于E, 于H,求证:
于H,求证: ;
;(3)如图3,在(2)的条件下,若
 平分
平分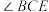 ,延长
,延长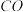 交
交 于P,
于P, ,
,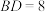 ,求
,求 长.
长.
更新时间:2023/12/15 00:44:01
|
相似题推荐
解答题-问答题
|
较难
(0.4)
名校
【推荐1】在平面直角坐标系中, 为坐标原点,直线
为坐标原点,直线 和
和 分别交
分别交 轴于
轴于 两点,交
两点,交 轴于
轴于 点,且
点,且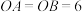 ,
,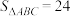 .
.
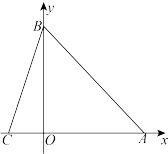
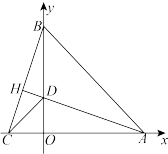
(1)如图1,求点 的坐标;
的坐标;
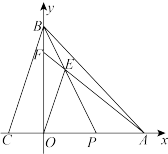
(2)如图2,过点 作
作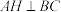 于
于 交
交 于点
于点 ,动点
,动点 从
从 点出发,以每秒1个单位长度的速度沿线段
点出发,以每秒1个单位长度的速度沿线段 向终点
向终点 运动,连接
运动,连接 、
、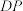 ,设
,设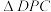 的面积为
的面积为 ,点
,点 的运动时间为
的运动时间为 ,求出
,求出 与
与 的关系式(用含
的关系式(用含 的式子表示
的式子表示 );
);
(3)如图3,在(2)的条件下,当 时,连接
时,连接 ,点
,点 为
为 上一点,射线
上一点,射线 交
交 轴于点
轴于点 ,连接
,连接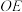 ,若
,若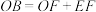 ,求
,求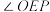 的度数.
的度数.
 为坐标原点,直线
为坐标原点,直线 和
和 分别交
分别交 轴于
轴于 两点,交
两点,交 轴于
轴于 点,且
点,且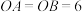 ,
,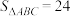 .
.


图1 图2 图3
(1)如图1,求点
 的坐标;
的坐标;(2)如图2,过点
 作
作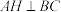 于
于 交
交 于点
于点 ,动点
,动点 从
从 点出发,以每秒1个单位长度的速度沿线段
点出发,以每秒1个单位长度的速度沿线段 向终点
向终点 运动,连接
运动,连接 、
、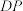 ,设
,设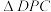 的面积为
的面积为 ,点
,点 的运动时间为
的运动时间为 ,求出
,求出 与
与 的关系式(用含
的关系式(用含 的式子表示
的式子表示 );
);(3)如图3,在(2)的条件下,当
 时,连接
时,连接 ,点
,点 为
为 上一点,射线
上一点,射线 交
交 轴于点
轴于点 ,连接
,连接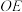 ,若
,若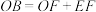 ,求
,求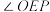 的度数.
的度数.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
【推荐2】如图1,平面直角坐标系中, 的直角顶点A在y轴正半轴上,设
的直角顶点A在y轴正半轴上,设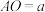 .
.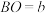 且a、b满足
且a、b满足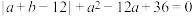

(1)求点C的坐标;
(2)如图2,点P在 上(点P不与O、C重合),连接
上(点P不与O、C重合),连接 ,
,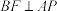 交
交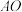 于点E,设点P的横坐标为t,
于点E,设点P的横坐标为t,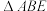 的面积为S,请用含t的代数式表示S;
的面积为S,请用含t的代数式表示S;
(3)如图3,在(2)的条件下,连接 ,
,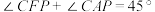 ,求点P的坐标.
,求点P的坐标.
 的直角顶点A在y轴正半轴上,设
的直角顶点A在y轴正半轴上,设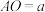 .
.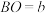 且a、b满足
且a、b满足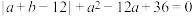

(1)求点C的坐标;
(2)如图2,点P在
 上(点P不与O、C重合),连接
上(点P不与O、C重合),连接 ,
,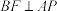 交
交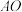 于点E,设点P的横坐标为t,
于点E,设点P的横坐标为t,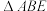 的面积为S,请用含t的代数式表示S;
的面积为S,请用含t的代数式表示S;(3)如图3,在(2)的条件下,连接
 ,
,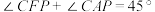 ,求点P的坐标.
,求点P的坐标.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
【推荐1】如图1,在平面直角坐标系中,直线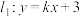 与直线
与直线 交于点A,已知点A的横坐标为
交于点A,已知点A的横坐标为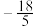 ,直线
,直线 与x轴交于点B,与y轴交于点C,直线
与x轴交于点B,与y轴交于点C,直线 与x轴交于点F,与y轴交于点D.
与x轴交于点F,与y轴交于点D.
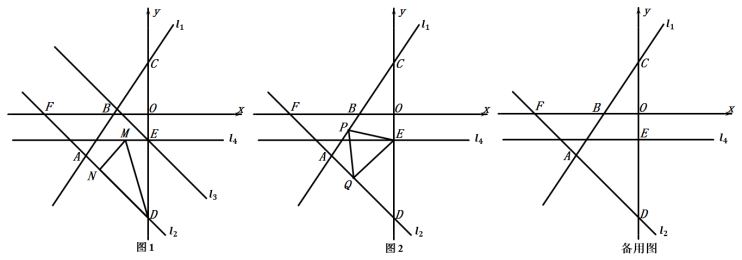
(1)求直线 的解析式;
的解析式;
(2)将直线 向上平移
向上平移 个单位得到直线
个单位得到直线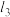 ,直线
,直线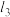 与y轴交于点E,过点E作y轴的垂线
与y轴交于点E,过点E作y轴的垂线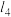 ,若点M为垂线
,若点M为垂线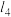 上的一个动点,点N为
上的一个动点,点N为 上的一个动点,求
上的一个动点,求 的最小值;
的最小值;
(3)已知点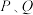 分别是直线
分别是直线 上的两个动点,连接
上的两个动点,连接 ,是否存在点
,是否存在点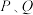 ,使得
,使得 是以点Q为直角顶点的等腰直角三角形,若存在,求点Q的坐标若不存在,说明理由.
是以点Q为直角顶点的等腰直角三角形,若存在,求点Q的坐标若不存在,说明理由.
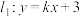 与直线
与直线 交于点A,已知点A的横坐标为
交于点A,已知点A的横坐标为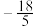 ,直线
,直线 与x轴交于点B,与y轴交于点C,直线
与x轴交于点B,与y轴交于点C,直线 与x轴交于点F,与y轴交于点D.
与x轴交于点F,与y轴交于点D.
(1)求直线
 的解析式;
的解析式;(2)将直线
 向上平移
向上平移 个单位得到直线
个单位得到直线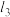 ,直线
,直线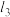 与y轴交于点E,过点E作y轴的垂线
与y轴交于点E,过点E作y轴的垂线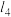 ,若点M为垂线
,若点M为垂线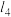 上的一个动点,点N为
上的一个动点,点N为 上的一个动点,求
上的一个动点,求 的最小值;
的最小值;(3)已知点
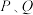 分别是直线
分别是直线 上的两个动点,连接
上的两个动点,连接 ,是否存在点
,是否存在点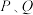 ,使得
,使得 是以点Q为直角顶点的等腰直角三角形,若存在,求点Q的坐标若不存在,说明理由.
是以点Q为直角顶点的等腰直角三角形,若存在,求点Q的坐标若不存在,说明理由.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
【推荐2】在直角坐标系中,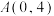 ,
,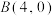 ,点
,点 分别是
分别是 轴,
轴, 轴上的动点,点
轴上的动点,点 在
在 的右侧,且
的右侧,且 ,连接
,连接 交直线
交直线 于点
于点 .
.
(1)如图1,当点 在线段
在线段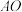 上运动时,线段
上运动时,线段 和线段
和线段 数量关系是 ;
数量关系是 ; 在射线
在射线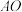 上运动时,如图2,线段
上运动时,如图2,线段 和线段
和线段 的关系有没有变化?(直接写出答案)
的关系有没有变化?(直接写出答案) ,当
,当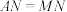 时,求
时,求 的长.
的长.
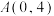 ,
,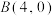 ,点
,点 分别是
分别是 轴,
轴, 轴上的动点,点
轴上的动点,点 在
在 的右侧,且
的右侧,且 ,连接
,连接 交直线
交直线 于点
于点 .
.(1)如图1,当点
 在线段
在线段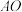 上运动时,线段
上运动时,线段 和线段
和线段 数量关系是 ;
数量关系是 ;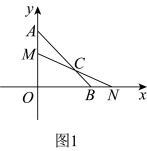
 在射线
在射线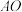 上运动时,如图2,线段
上运动时,如图2,线段 和线段
和线段 的关系有没有变化?(直接写出答案)
的关系有没有变化?(直接写出答案)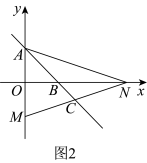
 ,当
,当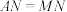 时,求
时,求 的长.
的长.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐1】如图,抛物线y=﹣(x+1)(x﹣3)与x轴分别交于点A、B(点A在B的右侧),与y轴交于点C,⊙P是△ABC的外接圆.
(1)直接写出点A、B、C的坐标及抛物线的对称轴;
(2)求⊙P的半径;
(3)点D在抛物线的对称轴上,且∠BDC>90°,求点D纵坐标的取值范围;
(4)E是线段CO上的一个动点,将线段AE绕点A逆时针旋转45°得线段AF,求线段OF的最小值.

(1)直接写出点A、B、C的坐标及抛物线的对称轴;
(2)求⊙P的半径;
(3)点D在抛物线的对称轴上,且∠BDC>90°,求点D纵坐标的取值范围;
(4)E是线段CO上的一个动点,将线段AE绕点A逆时针旋转45°得线段AF,求线段OF的最小值.

您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
【推荐2】定义:若两个三角形中,有两组边对应相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为偏等三角形.
(1)如图1,点 是弧
是弧 的中点,
的中点,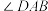 是弧
是弧 所对的圆周角,
所对的圆周角,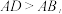 连接
连接 、
、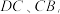 试说明
试说明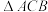 与
与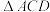 是偏等三角形.
是偏等三角形.

(2)如图2, 与
与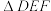 是偏等三角形,其中
是偏等三角形,其中 猜想结论:一对偏等三角形中,一组等边的对角相等,另一组等边的对角 .请填写结论,并说明理由.(以
猜想结论:一对偏等三角形中,一组等边的对角相等,另一组等边的对角 .请填写结论,并说明理由.(以 与
与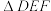 为例说明);
为例说明);

(3)如图3, 内接于
内接于 若点
若点 在
在 上,且
上,且 与
与 是偏等三角形,
是偏等三角形,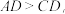 求
求 的值.
的值.

(1)如图1,点
 是弧
是弧 的中点,
的中点,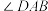 是弧
是弧 所对的圆周角,
所对的圆周角,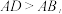 连接
连接 、
、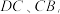 试说明
试说明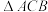 与
与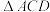 是偏等三角形.
是偏等三角形.
(2)如图2,
 与
与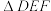 是偏等三角形,其中
是偏等三角形,其中 猜想结论:一对偏等三角形中,一组等边的对角相等,另一组等边的对角 .请填写结论,并说明理由.(以
猜想结论:一对偏等三角形中,一组等边的对角相等,另一组等边的对角 .请填写结论,并说明理由.(以 与
与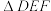 为例说明);
为例说明);
(3)如图3,
 内接于
内接于 若点
若点 在
在 上,且
上,且 与
与 是偏等三角形,
是偏等三角形,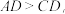 求
求 的值.
的值.
您最近一年使用:0次
【推荐1】如图,在等边△ABC中,点D、E分别在边AB、BC上,AD=BE,CD与AE交于F.
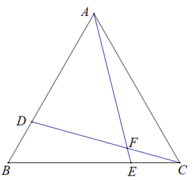
(1)求∠AFD的度数;
(2)若BE=m,CE=n.
①求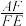 的值;(用含有m和n的式子表示)
的值;(用含有m和n的式子表示)
②若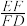 =
=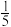 ,直接写出
,直接写出 的值.
的值.

(1)求∠AFD的度数;
(2)若BE=m,CE=n.
①求
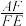 的值;(用含有m和n的式子表示)
的值;(用含有m和n的式子表示)②若
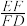 =
=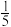 ,直接写出
,直接写出 的值.
的值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
解题方法
【推荐2】已知,如图1,抛物线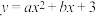 与
与 轴交于点
轴交于点 、
、 ,与
,与 轴交于点
轴交于点 ,且
,且 ,
,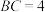 .
.

(1)求抛物线解析式;
(2)如图2,点 是抛物线第一象限上一点,连接
是抛物线第一象限上一点,连接 交
交 轴于点
轴于点 ,设点
,设点 的横坐标为
的横坐标为 ,线段
,线段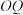 长为
长为 ,求
,求 与
与 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,过点 作直线
作直线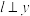 轴,在
轴,在 上取一点
上取一点 (点
(点 在第二象限),连接
在第二象限),连接 ,使
,使 ,连接
,连接 并延长
并延长 交
交 轴于点
轴于点 ,过点
,过点 作
作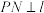 于点
于点 ,连接
,连接 、
、 、
、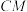 .若
.若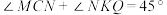 时,求
时,求 值.
值.
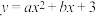 与
与 轴交于点
轴交于点 、
、 ,与
,与 轴交于点
轴交于点 ,且
,且 ,
,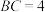 .
.
(1)求抛物线解析式;
(2)如图2,点
 是抛物线第一象限上一点,连接
是抛物线第一象限上一点,连接 交
交 轴于点
轴于点 ,设点
,设点 的横坐标为
的横坐标为 ,线段
,线段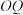 长为
长为 ,求
,求 与
与 之间的函数关系式;
之间的函数关系式;(3)在(2)的条件下,过点
 作直线
作直线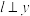 轴,在
轴,在 上取一点
上取一点 (点
(点 在第二象限),连接
在第二象限),连接 ,使
,使 ,连接
,连接 并延长
并延长 交
交 轴于点
轴于点 ,过点
,过点 作
作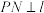 于点
于点 ,连接
,连接 、
、 、
、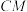 .若
.若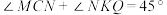 时,求
时,求 值.
值.
您最近一年使用:0次

 ,垂足为点
,垂足为点 ,
, 上一点,连接
上一点,连接 ,
, .
.
 ,求证∶
,求证∶ ;
; ,
, ,垂足为点
,垂足为点 ,连接
,连接 交
交 中点,求证∶
中点,求证∶ .
.
 中,
中, ,
, ,
, ,
,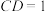 ,
, ,
,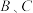 不重合,连接
不重合,连接 ,过
,过 交
交 所在直线于
所在直线于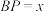 ,
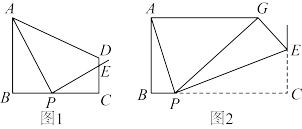
,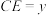 .
.
 的取值范围;
的取值范围; ,将
,将 沿
沿 翻折至
翻折至 位置,
位置,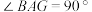 ,求
,求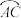 的中点时,求∠COB的度数;
的中点时,求∠COB的度数;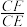 =y,求y关于x函数解析式,并写出定义域;
=y,求y关于x函数解析式,并写出定义域;
 ,用无刻度直尺和圆规求作线段
,用无刻度直尺和圆规求作线段 ,使得
,使得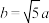 .(不写作法,保留作图痕迹)
.(不写作法,保留作图痕迹)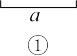
 的等㙘三角形称为“锐角黄金三角形”.
的等㙘三角形称为“锐角黄金三角形”. 都是锐角黄金三角形.求证:
都是锐角黄金三角形.求证: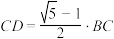 .
.