名校
解题方法
1 . 焦距为2c的椭圆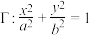 (a>b>0),如果满足“2b=a+c”,则称此椭圆为“等差椭圆”.
(a>b>0),如果满足“2b=a+c”,则称此椭圆为“等差椭圆”.
(1)如果椭圆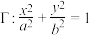 (a>b>0)是“等差椭圆”,求
(a>b>0)是“等差椭圆”,求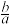 的值;
的值;
(2)对于焦距为12的“等差椭圆”,点A为椭圆短轴的上顶点,P为椭圆上异于A点的任一点,Q为P关于原点O的对称点(Q也异于A),直线AP、AQ分别与x轴交于M、N两点,判断以线段MN为直径的圆是否过定点?说明理由.
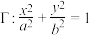 (a>b>0),如果满足“2b=a+c”,则称此椭圆为“等差椭圆”.
(a>b>0),如果满足“2b=a+c”,则称此椭圆为“等差椭圆”.(1)如果椭圆
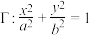 (a>b>0)是“等差椭圆”,求
(a>b>0)是“等差椭圆”,求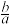 的值;
的值;(2)对于焦距为12的“等差椭圆”,点A为椭圆短轴的上顶点,P为椭圆上异于A点的任一点,Q为P关于原点O的对称点(Q也异于A),直线AP、AQ分别与x轴交于M、N两点,判断以线段MN为直径的圆是否过定点?说明理由.
您最近一年使用:0次
2022-05-14更新
|
1023次组卷
|
6卷引用:高考新题型-圆锥曲线
高考新题型-圆锥曲线(已下线)第25讲 圆锥曲线直线圆过定点问题-【同步题型讲义】2022-2023学年高二数学同步教学题型讲义(人教A版2019选择性必修第一册)(已下线)重难专攻(十)圆锥曲线中的定点问题 讲(已下线)压轴题圆锥曲线新定义题(九省联考第19题模式)练(已下线)大招4 圆锥曲线创新问题的速破策略江苏省盐城市滨海中学2019-2020学年高二下学期期末模拟数学试题
2 . 已知椭圆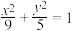 .
.
(1)动直线 垂直于
垂直于 轴,交椭圆于
轴,交椭圆于 、
、 两点,
两点, 、
、 两点分别和椭圆长轴的两个端点
两点分别和椭圆长轴的两个端点 、
、 的连线
的连线 、
、 相交于点
相交于点 ,求动点
,求动点 的轨迹方程;
的轨迹方程;
(2)若第(1)题所求出的轨迹称为椭圆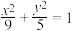 的“伴随曲线”,请你给出椭圆
的“伴随曲线”,请你给出椭圆 伴随曲线的定义及其方程.
伴随曲线的定义及其方程.
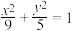 .
.(1)动直线
 垂直于
垂直于 轴,交椭圆于
轴,交椭圆于 、
、 两点,
两点, 、
、 两点分别和椭圆长轴的两个端点
两点分别和椭圆长轴的两个端点 、
、 的连线
的连线 、
、 相交于点
相交于点 ,求动点
,求动点 的轨迹方程;
的轨迹方程;(2)若第(1)题所求出的轨迹称为椭圆
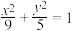 的“伴随曲线”,请你给出椭圆
的“伴随曲线”,请你给出椭圆 伴随曲线的定义及其方程.
伴随曲线的定义及其方程.
您最近一年使用:0次
3 . 定义:若点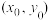 ,
,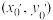 在椭圆
在椭圆 上,并且满足
上,并且满足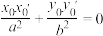 ,则称这两点是关于M的一对共轭点,或称点
,则称这两点是关于M的一对共轭点,或称点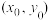 关于M的一个共轭点为
关于M的一个共轭点为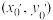 .已知点
.已知点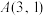 在椭圆
在椭圆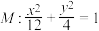 ,O坐标原点.
,O坐标原点.
(1)求点A关于M的所有共轭点的坐标;
(2)设点P,Q在M上,且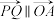 ,求点A关于M的所有共轭点和点P,Q所围成封闭图形面积的最大值.
,求点A关于M的所有共轭点和点P,Q所围成封闭图形面积的最大值.
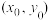 ,
,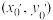 在椭圆
在椭圆 上,并且满足
上,并且满足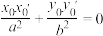 ,则称这两点是关于M的一对共轭点,或称点
,则称这两点是关于M的一对共轭点,或称点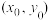 关于M的一个共轭点为
关于M的一个共轭点为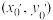 .已知点
.已知点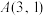 在椭圆
在椭圆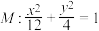 ,O坐标原点.
,O坐标原点.(1)求点A关于M的所有共轭点的坐标;
(2)设点P,Q在M上,且
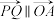 ,求点A关于M的所有共轭点和点P,Q所围成封闭图形面积的最大值.
,求点A关于M的所有共轭点和点P,Q所围成封闭图形面积的最大值.
您最近一年使用:0次
2022-02-21更新
|
1285次组卷
|
3卷引用:福建省福州市2022届高三上学期期末质量抽测数学试题
名校
解题方法
4 . 给出如下的定义和定理:定义:若直线l与抛物线 有且仅有一个公共点P,且l与
有且仅有一个公共点P,且l与 的对称轴不平行,则称直线l与抛物线
的对称轴不平行,则称直线l与抛物线 相切,公共点P称为切点.定理:过抛物线
相切,公共点P称为切点.定理:过抛物线 上一点
上一点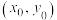 处的切线方程为
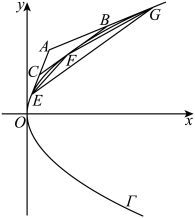
处的切线方程为 .完成下述问题:如图所示,设E,F是抛物线
.完成下述问题:如图所示,设E,F是抛物线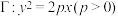 上两点.过点E,F分别作抛物线
上两点.过点E,F分别作抛物线 的两条切线
的两条切线 ,
, ,直线
,直线 ,
, 交于点C,点A,B分别在线段
交于点C,点A,B分别在线段 ,
, 的延长线上,且满足
的延长线上,且满足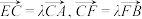 ,其中
,其中 .
.
(1)若点E,F的纵坐标分别为 ,
, ,用
,用 ,
, 和p表示点C的坐标.
和p表示点C的坐标.
(2)证明:直线 与抛物线
与抛物线 相切;
相切;
(3)设直线 与抛物线
与抛物线 相切于点G,求
相切于点G,求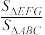 .
.
 有且仅有一个公共点P,且l与
有且仅有一个公共点P,且l与 的对称轴不平行,则称直线l与抛物线
的对称轴不平行,则称直线l与抛物线 相切,公共点P称为切点.定理:过抛物线
相切,公共点P称为切点.定理:过抛物线 上一点
上一点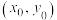 处的切线方程为
处的切线方程为 .完成下述问题:如图所示,设E,F是抛物线
.完成下述问题:如图所示,设E,F是抛物线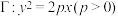 上两点.过点E,F分别作抛物线
上两点.过点E,F分别作抛物线 的两条切线
的两条切线 ,
, ,直线
,直线 ,
, 交于点C,点A,B分别在线段
交于点C,点A,B分别在线段 ,
, 的延长线上,且满足
的延长线上,且满足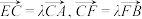 ,其中
,其中 .
.
(1)若点E,F的纵坐标分别为
 ,
, ,用
,用 ,
, 和p表示点C的坐标.
和p表示点C的坐标.(2)证明:直线
 与抛物线
与抛物线 相切;
相切;(3)设直线
 与抛物线
与抛物线 相切于点G,求
相切于点G,求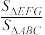 .
.
您最近一年使用:0次
2022-01-16更新
|
752次组卷
|
4卷引用:上海市复旦大学附属中学2021-2022学年高二上学期期末数学试题
上海市复旦大学附属中学2021-2022学年高二上学期期末数学试题高考新题型-圆锥曲线(已下线)期末真题必刷压轴60题(22个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)压轴题圆锥曲线新定义题(九省联考第19题模式)练
5 . 已知椭圆 :
: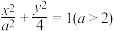 ,点
,点 为椭圆短轴的上端点,
为椭圆短轴的上端点, 为椭圆上异于
为椭圆上异于 点的任一点,若
点的任一点,若 点到
点到 点距离的最大值仅在
点距离的最大值仅在 点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”.
点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”.
(1)若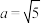 ,判断椭圆
,判断椭圆 是否为“圆椭圆”;
是否为“圆椭圆”;
(2)若椭圆 是“圆椭圆”,求
是“圆椭圆”,求 的取值范围.
的取值范围.
 :
: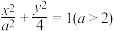 ,点
,点 为椭圆短轴的上端点,
为椭圆短轴的上端点, 为椭圆上异于
为椭圆上异于 点的任一点,若
点的任一点,若 点到
点到 点距离的最大值仅在
点距离的最大值仅在 点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”.
点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”.(1)若
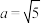 ,判断椭圆
,判断椭圆 是否为“圆椭圆”;
是否为“圆椭圆”;(2)若椭圆
 是“圆椭圆”,求
是“圆椭圆”,求 的取值范围.
的取值范围.
您最近一年使用:0次
2021-10-20更新
|
378次组卷
|
2卷引用:2023版 苏教版(2019) 选修第一册 突围者 第3章 第一节 课时2 椭圆的几何性质
2022·福建·模拟预测
6 . 等轴双曲线是离心率为 的双曲线,可建立合适的坐标平面使之为反比例函数.
的双曲线,可建立合适的坐标平面使之为反比例函数.
(1)在等轴双曲线 上有三点
上有三点 ,
, ,
, ,其横坐标依次是
,其横坐标依次是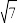 ,
, ,
, .设
.设 ,
, ,
, 分别为
分别为 ,
, ,
, 的中点,试求
的中点,试求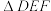 的外接圆圆心的横坐标.
的外接圆圆心的横坐标.
(2)双曲线 的渐近线为
的渐近线为 和
和 ,
, 上有三个不同的点
上有三个不同的点 ,
, ,
, ,直线
,直线 、直线
、直线 、直线
、直线 与
与 分别交于
分别交于 ,
, ,
, ,过
,过 ,
, ,
, 分别作直线
分别作直线 、直线
、直线 、直线
、直线 的垂线
的垂线 ,
,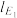 ,
,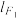 .
.
(i)当 为等轴双曲线时,证明:
为等轴双曲线时,证明: ,
,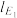 ,
,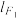 三线共点.
三线共点.
(ii)当 不为等轴双曲线时,记
不为等轴双曲线时,记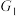 ,
,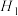 ,
,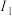 分别是
分别是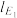 与
与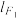 ,
,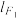 与
与 ,
, 与
与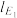 的交点,类似地从另一条渐近线
的交点,类似地从另一条渐近线 出发来定义
出发来定义 ,
,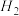 ,
,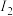 .证明:
.证明: .
.
 的双曲线,可建立合适的坐标平面使之为反比例函数.
的双曲线,可建立合适的坐标平面使之为反比例函数.(1)在等轴双曲线
 上有三点
上有三点 ,
, ,
, ,其横坐标依次是
,其横坐标依次是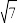 ,
, ,
, .设
.设 ,
, ,
, 分别为
分别为 ,
, ,
, 的中点,试求
的中点,试求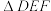 的外接圆圆心的横坐标.
的外接圆圆心的横坐标.(2)双曲线
 的渐近线为
的渐近线为 和
和 ,
, 上有三个不同的点
上有三个不同的点 ,
, ,
, ,直线
,直线 、直线
、直线 、直线
、直线 与
与 分别交于
分别交于 ,
, ,
, ,过
,过 ,
, ,
, 分别作直线
分别作直线 、直线
、直线 、直线
、直线 的垂线
的垂线 ,
,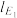 ,
,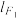 .
.(i)当
 为等轴双曲线时,证明:
为等轴双曲线时,证明: ,
,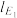 ,
,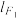 三线共点.
三线共点.(ii)当
 不为等轴双曲线时,记
不为等轴双曲线时,记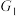 ,
,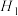 ,
,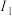 分别是
分别是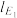 与
与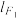 ,
,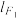 与
与 ,
, 与
与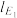 的交点,类似地从另一条渐近线
的交点,类似地从另一条渐近线 出发来定义
出发来定义 ,
,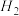 ,
,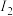 .证明:
.证明: .
.
您最近一年使用:0次
2021-09-03更新
|
1072次组卷
|
4卷引用:专题13 圆锥曲线-备战2022年高考数学(文)母题题源解密(全国乙卷)
20-21高二下·重庆渝中·期末
名校
解题方法
7 . 阿波罗尼斯是古希腊著名数学家,他的主要研究成果集中在他的代表作《圆锥曲线》一书中.阿波罗尼斯圆是他的研究成果之一,指的是已知动点 与两定点
与两定点 ,
, 的距离之比
的距离之比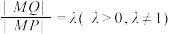 ,
, 是一个常数,那么动点
是一个常数,那么动点 的轨迹就是阿波罗尼斯圆,圆心在直线
的轨迹就是阿波罗尼斯圆,圆心在直线 上.已知动点
上.已知动点 的轨迹是阿波罗尼斯圆,其方程为
的轨迹是阿波罗尼斯圆,其方程为 ,定点分别为椭圆
,定点分别为椭圆 的右焦点
的右焦点 与右顶点
与右顶点 ,且椭圆
,且椭圆 的离心率为
的离心率为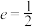 .
. 的标准方程;
的标准方程;
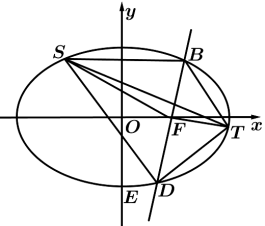
(2)如图,过右焦点 斜率为
斜率为 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, (点
(点 在
在 轴上方),点
轴上方),点 ,
, 是椭圆
是椭圆 上异于
上异于 ,
, 的两点,
的两点,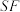 平分
平分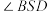 ,
,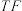 平分
平分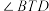 .
.
①求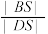 的取值范围;
的取值范围;
②将点 、
、 、
、 看作一个阿波罗尼斯圆上的三点,若
看作一个阿波罗尼斯圆上的三点,若 外接圆的面积为
外接圆的面积为 ,求直线
,求直线 的方程.
的方程.
 与两定点
与两定点 ,
, 的距离之比
的距离之比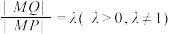 ,
, 是一个常数,那么动点
是一个常数,那么动点 的轨迹就是阿波罗尼斯圆,圆心在直线
的轨迹就是阿波罗尼斯圆,圆心在直线 上.已知动点
上.已知动点 的轨迹是阿波罗尼斯圆,其方程为
的轨迹是阿波罗尼斯圆,其方程为 ,定点分别为椭圆
,定点分别为椭圆 的右焦点
的右焦点 与右顶点
与右顶点 ,且椭圆
,且椭圆 的离心率为
的离心率为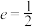 .
.
 的标准方程;
的标准方程;(2)如图,过右焦点
 斜率为
斜率为 的直线
的直线 与椭圆
与椭圆 相交于
相交于 ,
, (点
(点 在
在 轴上方),点
轴上方),点 ,
, 是椭圆
是椭圆 上异于
上异于 ,
, 的两点,
的两点,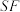 平分
平分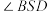 ,
,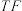 平分
平分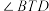 .
.①求
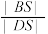 的取值范围;
的取值范围;②将点
 、
、 、
、 看作一个阿波罗尼斯圆上的三点,若
看作一个阿波罗尼斯圆上的三点,若 外接圆的面积为
外接圆的面积为 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2021-07-12更新
|
5147次组卷
|
11卷引用:专题1 阿波罗尼斯圆及其应用 微点4 阿波罗尼斯圆与圆锥曲线
(已下线)专题1 阿波罗尼斯圆及其应用 微点4 阿波罗尼斯圆与圆锥曲线重庆市巴蜀中学2020-2021学年高二下学期期末数学试题(已下线)专题12 圆锥曲线的方程的压轴题(二)-【尖子生专用】2021-2022学年高二数学考点培优训练(人教A版2019选择性必修第一册)重庆市南开中学校2023届高三上学期期末数学试题安徽省合肥一六八中学等学校2024届高三上学期名校期末联合测试数学试题(已下线)圆锥曲线新定义河南省信阳市新县高级中学2024届高三考前第三次适应性考试数学试题(已下线)第3章 圆锥曲线与方程 单元综合检测(能力提升)(单元培优)-2021-2022学年高二数学课后培优练(苏教版2019选择性必修第一册)(已下线)专题08 《圆锥曲线与方程》中的解答题压轴题(2)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册) 安徽“耀正优+”2024届高三名校上学期期末测试数学试题(已下线)信息必刷卷01(江苏专用,2024新题型)
名校
解题方法
8 . 已知椭圆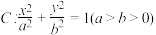 的右焦点为F(1,0),且点
的右焦点为F(1,0),且点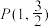 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)过椭圆 上异于其顶点的任意一点Q作圆
上异于其顶点的任意一点Q作圆 的两条切线,切点分别为M,N(M,N不在坐标轴上),若直线MN在x轴,y轴上的截距分别为m,n,证明:
的两条切线,切点分别为M,N(M,N不在坐标轴上),若直线MN在x轴,y轴上的截距分别为m,n,证明: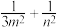 为定值;
为定值;
(3)若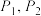 是椭圆
是椭圆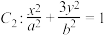 上不同的两点,
上不同的两点,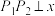 轴,圆E过
轴,圆E过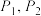 且椭圆
且椭圆 上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆.试问:椭圆
上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆.试问:椭圆 是否存在过左焦点
是否存在过左焦点 的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
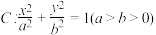 的右焦点为F(1,0),且点
的右焦点为F(1,0),且点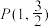 在椭圆C上.
在椭圆C上.(1)求椭圆C的标准方程;
(2)过椭圆
 上异于其顶点的任意一点Q作圆
上异于其顶点的任意一点Q作圆 的两条切线,切点分别为M,N(M,N不在坐标轴上),若直线MN在x轴,y轴上的截距分别为m,n,证明:
的两条切线,切点分别为M,N(M,N不在坐标轴上),若直线MN在x轴,y轴上的截距分别为m,n,证明: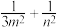 为定值;
为定值;(3)若
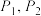 是椭圆
是椭圆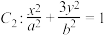 上不同的两点,
上不同的两点,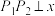 轴,圆E过
轴,圆E过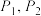 且椭圆
且椭圆 上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆.试问:椭圆
上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆.试问:椭圆 是否存在过左焦点
是否存在过左焦点 的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
您最近一年使用:0次
2020-11-15更新
|
2258次组卷
|
5卷引用:辽宁省部分中学2021-2022学年高三下学期期末数学试题
辽宁省部分中学2021-2022学年高三下学期期末数学试题(已下线)专题24 圆锥曲线中的存在性、探索性问题 微点1 圆锥曲线中的存在性问题上海市南洋模范中学2021届高三上学期期中数学试题上海市宜川中学2022-2023学年高二下学期数学期末模拟测试卷2(已下线)圆锥曲线新定义
19-20高三上·上海徐汇·阶段练习
名校
9 . 已知椭圆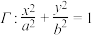 (
( ),点
),点 为椭圆短轴的上端点,
为椭圆短轴的上端点, 为椭圆上异于
为椭圆上异于 点的任一点,若
点的任一点,若 点到
点到 点距离的最大值仅在
点距离的最大值仅在 点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”,已知
点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”,已知 .
.
(1)若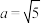 ,判断椭圆
,判断椭圆 是否为“圆椭圆”;
是否为“圆椭圆”;
(2)若椭圆 是“圆椭圆”,求
是“圆椭圆”,求 的取值范围;
的取值范围;
(3)若椭圆 是“圆椭圆”,且
是“圆椭圆”,且 取最大值,
取最大值, 为
为 关于原点
关于原点 的对称点,
的对称点, 也异于
也异于 点,直线
点,直线 、
、 分别与
分别与 轴交于
轴交于 、
、 两点,试问以线段
两点,试问以线段 为直径的圆是否过定点?证明你的结论.
为直径的圆是否过定点?证明你的结论.
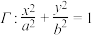 (
( ),点
),点 为椭圆短轴的上端点,
为椭圆短轴的上端点, 为椭圆上异于
为椭圆上异于 点的任一点,若
点的任一点,若 点到
点到 点距离的最大值仅在
点距离的最大值仅在 点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”,已知
点为短轴的另一端点时取到,则称此椭圆为“圆椭圆”,已知 .
.(1)若
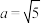 ,判断椭圆
,判断椭圆 是否为“圆椭圆”;
是否为“圆椭圆”;(2)若椭圆
 是“圆椭圆”,求
是“圆椭圆”,求 的取值范围;
的取值范围;(3)若椭圆
 是“圆椭圆”,且
是“圆椭圆”,且 取最大值,
取最大值, 为
为 关于原点
关于原点 的对称点,
的对称点, 也异于
也异于 点,直线
点,直线 、
、 分别与
分别与 轴交于
轴交于 、
、 两点,试问以线段
两点,试问以线段 为直径的圆是否过定点?证明你的结论.
为直径的圆是否过定点?证明你的结论.
您最近一年使用:0次
2020-01-13更新
|
682次组卷
|
7卷引用:考向04 一次函数与二次函数-备战2022年高考数学一轮复习考点微专题(上海专用)
(已下线)考向04 一次函数与二次函数-备战2022年高考数学一轮复习考点微专题(上海专用)(已下线)第13讲 椭圆 - 1重庆市江津中学2022-2023学年高二上学期10月阶段性考试数学试题上海市徐汇区2019-2020学年高三上学期第一次模拟数学试题(已下线)压轴题圆锥曲线新定义题(九省联考第19题模式)练上海市七宝中学2023-2024学年高二下学期3月月考数学试题(已下线)江苏省南通市如皋市2021-2022学年高二上学期第一次调研测试模拟演练数学试题
名校
10 . (1)设椭圆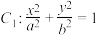 与双曲线
与双曲线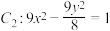 有相同的焦点
有相同的焦点 、
、 ,
, 是椭圆
是椭圆 与双曲线
与双曲线 的公共点,且△
的公共点,且△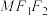 的周长为6,求椭圆
的周长为6,求椭圆 的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;
的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;
(2)如图,已知“盾圆 ”的方程为
”的方程为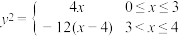 ,设“盾圆
,设“盾圆 ”上的任意一点
”上的任意一点 到
到 的距离为
的距离为 ,
, 到直线
到直线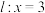 的距离为
的距离为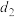 ,求证:
,求证: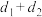 为定值;
为定值;

(3)由抛物线弧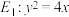 (
(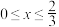 )与第(1)小题椭圆弧
)与第(1)小题椭圆弧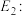
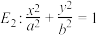 (
(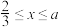 )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆 ”,设过点
”,设过点 的直线与“盾圆
的直线与“盾圆 ”交于
”交于 、
、 两点,
两点,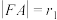 ,
,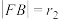 ,且
,且 (
( ),试用
),试用 表示
表示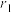 ,并求
,并求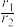 的取值范围.
的取值范围.
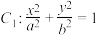 与双曲线
与双曲线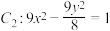 有相同的焦点
有相同的焦点 、
、 ,
, 是椭圆
是椭圆 与双曲线
与双曲线 的公共点,且△
的公共点,且△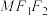 的周长为6,求椭圆
的周长为6,求椭圆 的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;
的方程;我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”;(2)如图,已知“盾圆
 ”的方程为
”的方程为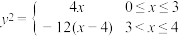 ,设“盾圆
,设“盾圆 ”上的任意一点
”上的任意一点 到
到 的距离为
的距离为 ,
, 到直线
到直线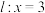 的距离为
的距离为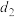 ,求证:
,求证: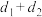 为定值;
为定值;
(3)由抛物线弧
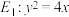 (
(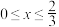 )与第(1)小题椭圆弧
)与第(1)小题椭圆弧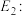
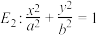 (
(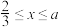 )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆 ”,设过点
”,设过点 的直线与“盾圆
的直线与“盾圆 ”交于
”交于 、
、 两点,
两点,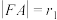 ,
,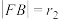 ,且
,且 (
( ),试用
),试用 表示
表示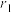 ,并求
,并求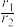 的取值范围.
的取值范围.
您最近一年使用:0次
2019-12-08更新
|
2171次组卷
|
5卷引用:上海市实验学校2022届高三冲刺模拟卷5数学试题
上海市实验学校2022届高三冲刺模拟卷5数学试题(已下线)专题17 椭圆与双曲线共焦点问题 微点4 椭圆与双曲线共焦点综合训练上海市复旦大学附属中学2018-2019学年高三上学期10月月考数学试题上海市延安中学2017届高三上学期开学考试数学试题(已下线)圆锥曲线新定义



