名校
解题方法
1 . 对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为: )为
)为 ,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为
,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为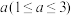 .设用
.设用 单位质量的水初次清洗后的清洁度是
单位质量的水初次清洗后的清洁度是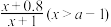 ,用
,用 单位质量的水第二次清洗后的清洁度是
单位质量的水第二次清洗后的清洁度是 ,其中
,其中 是该物体初次清洗后的清洁度.
是该物体初次清洗后的清洁度.
(1)分别求出方案甲以及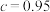 时方案乙的用水量,并比较哪一种方案用水量较少;
时方案乙的用水量,并比较哪一种方案用水量较少;
(2)若采用方案乙, 为定值,当
为定值,当 为何值时,总用水量最少?并讨论
为何值时,总用水量最少?并讨论 取不同数值时,对最少总用水量多少的影响.
取不同数值时,对最少总用水量多少的影响.
 )为
)为 ,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为
,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为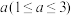 .设用
.设用 单位质量的水初次清洗后的清洁度是
单位质量的水初次清洗后的清洁度是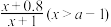 ,用
,用 单位质量的水第二次清洗后的清洁度是
单位质量的水第二次清洗后的清洁度是 ,其中
,其中 是该物体初次清洗后的清洁度.
是该物体初次清洗后的清洁度.(1)分别求出方案甲以及
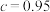 时方案乙的用水量,并比较哪一种方案用水量较少;
时方案乙的用水量,并比较哪一种方案用水量较少;(2)若采用方案乙,
 为定值,当
为定值,当 为何值时,总用水量最少?并讨论
为何值时,总用水量最少?并讨论 取不同数值时,对最少总用水量多少的影响.
取不同数值时,对最少总用水量多少的影响.
您最近一年使用:0次
名校
解题方法
2 . 某高校就业部从该校2022年已就业的博士研究生的毕业生中随机抽取了200人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率分布直方图:
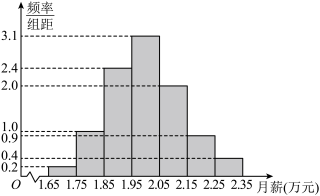
(1)将同一组数据用该区间的中点值作代表,求这200人月薪收入的样本平均数 ;
;
(2)该校在某地区就业的2022届博士研究生的毕业生共100人,决定于2023年五一劳动节长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设区间 ,月薪落在区间
,月薪落在区间 左侧的每人收取400元,月薪落在区间
左侧的每人收取400元,月薪落在区间 内的每人收取600元,月薪落在区间
内的每人收取600元,月薪落在区间 右侧的每人收取800元;
右侧的每人收取800元;
方案二:每人按月薪收入的样本平均数的3%收取;
用该校就业部统计的这200人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用?

(1)将同一组数据用该区间的中点值作代表,求这200人月薪收入的样本平均数
 ;
;(2)该校在某地区就业的2022届博士研究生的毕业生共100人,决定于2023年五一劳动节长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设区间
 ,月薪落在区间
,月薪落在区间 左侧的每人收取400元,月薪落在区间
左侧的每人收取400元,月薪落在区间 内的每人收取600元,月薪落在区间
内的每人收取600元,月薪落在区间 右侧的每人收取800元;
右侧的每人收取800元;方案二:每人按月薪收入的样本平均数的3%收取;
用该校就业部统计的这200人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用?
您最近一年使用:0次
2023-07-28更新
|
239次组卷
|
2卷引用:黑龙江省克东县第一中学、克东县职业技术学校2022-2023学年高二下学期3月质量监测数学试题
名校
3 . 为普及航空航天科技相关知识、发展青少年航空航天科学素养,贵州省某中学组织开展“筑梦空天”航空航天知识竞赛.竞赛试题有甲、乙、丙三类(每类题有若干道),各类试题的每题分值及小明答对概率如下表所示,各小题回答正确得到相应分值,否则得 分,竞赛分三轮答题依次进行,各轮得分之和即为选手总分.
分,竞赛分三轮答题依次进行,各轮得分之和即为选手总分.
其竞赛规则为:
第一轮,先回答一道甲类题,若正确,进入第二轮答题;若错误,继续回答另一道甲类题,该题回答正确,同样进入第二轮答题,否则,退出比赛.
第二轮,在乙类题或丙类题中选择一道作答,若正确,进入第三轮答题;否则,退出比赛.
第三轮,在前两轮未作答的那一类试题中选择一道作答.
小明参加竞赛,有两种方案选择,方案一:先答甲类题,再答乙类题,最后答丙类题;
方案二:先答甲类题,再答丙类题,最后答乙类题.各题答对与否互不影响.请完成以下解答:
(1)若小明选择方案一,求答题次数恰好为 次的概率;
次的概率;
(2)经计算小明选择方案一所得总分的数学期望为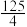 ,为使所得总分的数学期望最大,小明该选择哪一种方案?并说明理由.
,为使所得总分的数学期望最大,小明该选择哪一种方案?并说明理由.
 分,竞赛分三轮答题依次进行,各轮得分之和即为选手总分.
分,竞赛分三轮答题依次进行,各轮得分之和即为选手总分.项目 题型 | 每小题分值 | 每小题答对概率 |
甲类题 |
|
|
乙类题 |
|
|
丙类题 |
|
|
第一轮,先回答一道甲类题,若正确,进入第二轮答题;若错误,继续回答另一道甲类题,该题回答正确,同样进入第二轮答题,否则,退出比赛.
第二轮,在乙类题或丙类题中选择一道作答,若正确,进入第三轮答题;否则,退出比赛.
第三轮,在前两轮未作答的那一类试题中选择一道作答.
小明参加竞赛,有两种方案选择,方案一:先答甲类题,再答乙类题,最后答丙类题;
方案二:先答甲类题,再答丙类题,最后答乙类题.各题答对与否互不影响.请完成以下解答:
(1)若小明选择方案一,求答题次数恰好为
 次的概率;
次的概率;(2)经计算小明选择方案一所得总分的数学期望为
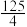 ,为使所得总分的数学期望最大,小明该选择哪一种方案?并说明理由.
,为使所得总分的数学期望最大,小明该选择哪一种方案?并说明理由.
您最近一年使用:0次
2023-04-10更新
|
979次组卷
|
3卷引用:黑龙江省哈尔滨市第九中学2023届高三第三次模拟考试数学试题
名校
4 . 我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于52棵,且用于购买这两种树苗的资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于52棵,且用于购买这两种树苗的资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
您最近一年使用:0次
名校
解题方法
5 . 统计某公司 名推销员的月销售额(单位:千元)得到如下频率分布直方图.
名推销员的月销售额(单位:千元)得到如下频率分布直方图.
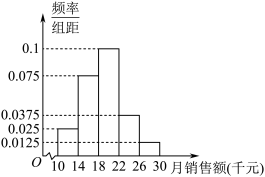
(1)同一组数据用该区间的中间值作代表,求这 名推销员的月销售额的平均数
名推销员的月销售额的平均数 与方差
与方差 ;
;
(2)请根据这组数据提出使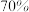 的推销员能够完成销售指标的建议;
的推销员能够完成销售指标的建议;
(3)现有两种奖励机制:
方案一:设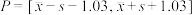 ,销售额落在
,销售额落在 左侧,每人每月奖励
左侧,每人每月奖励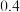 千元;销售额落在
千元;销售额落在 内,每人每月奖励
内,每人每月奖励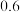 千元;销售额落在
千元;销售额落在 右侧,每人每月奖励
右侧,每人每月奖励 千元.
千元.
方案二:每人每月奖励其月销售额的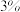 .
.
用统计的频率进行估算,选择哪一种方案公司需提供更多的奖励金?(参考数据: )
)
记: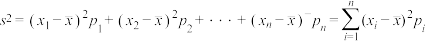 (其中
(其中 为
为 对应的频率).
对应的频率).
 名推销员的月销售额(单位:千元)得到如下频率分布直方图.
名推销员的月销售额(单位:千元)得到如下频率分布直方图.
(1)同一组数据用该区间的中间值作代表,求这
 名推销员的月销售额的平均数
名推销员的月销售额的平均数 与方差
与方差 ;
;(2)请根据这组数据提出使
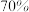 的推销员能够完成销售指标的建议;
的推销员能够完成销售指标的建议;(3)现有两种奖励机制:
方案一:设
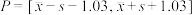 ,销售额落在
,销售额落在 左侧,每人每月奖励
左侧,每人每月奖励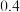 千元;销售额落在
千元;销售额落在 内,每人每月奖励
内,每人每月奖励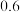 千元;销售额落在
千元;销售额落在 右侧,每人每月奖励
右侧,每人每月奖励 千元.
千元.方案二:每人每月奖励其月销售额的
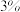 .
.用统计的频率进行估算,选择哪一种方案公司需提供更多的奖励金?(参考数据:
 )
)记:
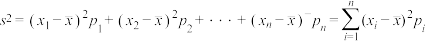 (其中
(其中 为
为 对应的频率).
对应的频率).
您最近一年使用:0次
2021-06-23更新
|
1352次组卷
|
5卷引用:黑龙江省哈尔滨市第四中学校2022-2023学年高二上学期第一次月考数学试题
黑龙江省哈尔滨市第四中学校2022-2023学年高二上学期第一次月考数学试题河南名校联盟2020-2021学年高一下学期期中考试数学(文)试题福建省泉州市永春第一中学2020-2021学年高一下学期期末数学试题(已下线)第九章 统计(选拔卷)-【单元测试】2021-2022学年高一数学尖子生选拔卷(人教A版2019必修第二册)江西省遂川中学2021-2022学年高一上学期第一次月考数学试题(A卷)
6 . 某专营店统计了最近 天到该店购物的人数
天到该店购物的人数 和时间第
和时间第 天之间的数据,列表如下:
天之间的数据,列表如下:
(1)由表中给出的数据,判断是否可用线性回归模型拟合人数 与时间
与时间 之间的关系?(若
之间的关系?(若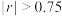 ,则认为线性相关程度高,可用线性回归模型拟合;否则,不可用线性回归模型拟合.计算
,则认为线性相关程度高,可用线性回归模型拟合;否则,不可用线性回归模型拟合.计算 时精确到
时精确到 )
)
(2)该专营店为了吸引顾客,推出两种促销方案:方案一,购物金额每满 元可减
元可减 元;方案二,购物金额超过
元;方案二,购物金额超过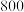 元可抽奖三次,每次中奖的概率均为
元可抽奖三次,每次中奖的概率均为 ,且每次抽奖互不影响,中奖一次打
,且每次抽奖互不影响,中奖一次打 折,中奖两次打
折,中奖两次打 折,中奖三次打
折,中奖三次打 折.某顾客计划在此专营店购买一件价值
折.某顾客计划在此专营店购买一件价值 元的商品,请从实际付款金额的数学期望的角度分析,选哪种方案更优惠?
元的商品,请从实际付款金额的数学期望的角度分析,选哪种方案更优惠?
参考数据: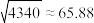 .附:相关系数
.附:相关系数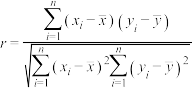 .
.
 天到该店购物的人数
天到该店购物的人数 和时间第
和时间第 天之间的数据,列表如下:
天之间的数据,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
 与时间
与时间 之间的关系?(若
之间的关系?(若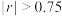 ,则认为线性相关程度高,可用线性回归模型拟合;否则,不可用线性回归模型拟合.计算
,则认为线性相关程度高,可用线性回归模型拟合;否则,不可用线性回归模型拟合.计算 时精确到
时精确到 )
)(2)该专营店为了吸引顾客,推出两种促销方案:方案一,购物金额每满
 元可减
元可减 元;方案二,购物金额超过
元;方案二,购物金额超过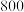 元可抽奖三次,每次中奖的概率均为
元可抽奖三次,每次中奖的概率均为 ,且每次抽奖互不影响,中奖一次打
,且每次抽奖互不影响,中奖一次打 折,中奖两次打
折,中奖两次打 折,中奖三次打
折,中奖三次打 折.某顾客计划在此专营店购买一件价值
折.某顾客计划在此专营店购买一件价值 元的商品,请从实际付款金额的数学期望的角度分析,选哪种方案更优惠?
元的商品,请从实际付款金额的数学期望的角度分析,选哪种方案更优惠?参考数据:
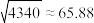 .附:相关系数
.附:相关系数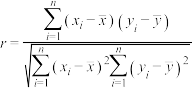 .
.
您最近一年使用:0次
2023-11-07更新
|
1083次组卷
|
11卷引用:黑龙江省大兴安岭实验中学(东校区)2024届高三上学期11月月考数学试题
黑龙江省大兴安岭实验中学(东校区)2024届高三上学期11月月考数学试题广东省广州市荔湾区2024届高三上学期十月月考数学试题(已下线)第十章 重难专攻(十三) 概率与统计的综合问题(讲)(已下线)第三节 成对数据的统计分析(第一课时) B卷素养养成卷 一轮复习点点通重庆市九龙坡区育才中学校2024届高三上学期第三次联考复习数学试题8.1.2样本相关系数练习(已下线)8.1 成对数据的统计相关性(分层练习,5大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)第01讲 8.1 成对数据的统计相关性(知识清单+5类热点题型精讲+强化分层精练)-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)8.1.1变量的相关关系+8.1.2样本相关系数 第三练 能力提升拔高(已下线)8.1 成对数据的统计相关性——课后作业(提升版)(已下线)8.1 成对数据的统计相关性——课后作业(巩固版)
名校
解题方法
7 . 目前脱贫攻坚进入决胜的关键阶段,某扶贫企业为了增加工作岗位和增加员工收入,决定投入90万元再上一套生产设备,预计使用该设备后前 年的支出成本为
年的支出成本为 万元,每年的销售收入95万元.
万元,每年的销售收入95万元.
(1)估计该设备从第几年开始实现总盈利;
(2)使用若干年后对该设备处理的方案有两种:
方案一:当总盈利额达到最大值时,该设备以20万元的价格处理;
方案二:当年平均盈利额达到最大值时,该设备以60万元的价格处理;
问哪种方案较为合理?并说明理由.
 年的支出成本为
年的支出成本为 万元,每年的销售收入95万元.
万元,每年的销售收入95万元.(1)估计该设备从第几年开始实现总盈利;
(2)使用若干年后对该设备处理的方案有两种:
方案一:当总盈利额达到最大值时,该设备以20万元的价格处理;
方案二:当年平均盈利额达到最大值时,该设备以60万元的价格处理;
问哪种方案较为合理?并说明理由.
您最近一年使用:0次
2023-02-26更新
|
100次组卷
|
3卷引用:黑龙江省牡丹江市第二高级中学2023-2024学年高一上学期10月月考数学试题
名校
解题方法
8 . 某公司为了让职工业余时间加强体育锻炼,修建了一个运动俱乐部,公司随机抽查了200名职工在修建运动俱乐部前后每天运动的时间,得到以下频数分布表:
表一(运动俱乐部修建前)
表二(运动俱乐部修建后)
(1)分别求出修建运动俱乐部前和修建运动俱乐部后职工每天运动的平均时间(同一时间段的数据取该组区间的中点值作代表)﹔
(2)运动俱乐部内有一套与室温调节有关的设备,内有2个完全一样的用电器A,只有这2个用电器A都正常工作时,整套设备才正常工作,且2个用电器A是否正常工作互不影响.用电器A有M,N两种品牌,M品牌的销售单价为1000元,正常工作寿命为11个月或12个月(概率均为 );N品牌的销售单价为400元,正常工作寿命为5个月或6个月(概率均为
);N品牌的销售单价为400元,正常工作寿命为5个月或6个月(概率均为 ).现有两种购置方案:
).现有两种购置方案:
方案1:购置2个M品牌用电器﹔
方案2:购置1个M品牌用电器和2个N品牌用电器(其中1个N品牌用电器不能正常工作时则使用另一个N品牌用电器).
试求两种方案各自设备性价比(设备正常运行时间与购置用电器A的成本比)的分布列,并从性价比的数学期望角度考虑,选择哪种方案更实惠?
表一(运动俱乐部修建前)
| 时间(分钟) |  |  | 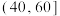 | 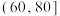 |
| 人数 | 36 | 58 | 81 | 25 |
| 时间(分钟) |  |  | 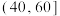 | 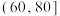 |
| 人数 | 18 | 63 | 83 | 36 |
(2)运动俱乐部内有一套与室温调节有关的设备,内有2个完全一样的用电器A,只有这2个用电器A都正常工作时,整套设备才正常工作,且2个用电器A是否正常工作互不影响.用电器A有M,N两种品牌,M品牌的销售单价为1000元,正常工作寿命为11个月或12个月(概率均为
 );N品牌的销售单价为400元,正常工作寿命为5个月或6个月(概率均为
);N品牌的销售单价为400元,正常工作寿命为5个月或6个月(概率均为 ).现有两种购置方案:
).现有两种购置方案:方案1:购置2个M品牌用电器﹔
方案2:购置1个M品牌用电器和2个N品牌用电器(其中1个N品牌用电器不能正常工作时则使用另一个N品牌用电器).
试求两种方案各自设备性价比(设备正常运行时间与购置用电器A的成本比)的分布列,并从性价比的数学期望角度考虑,选择哪种方案更实惠?
您最近一年使用:0次
2023-05-19更新
|
525次组卷
|
5卷引用:黑龙江省大庆市肇州县第二中学2022-2023学年高二下学期期中数学试题
名校
9 . 2021年新高考数学试卷中对每道多选题的得分规定:全部选对的得5分,部分选对的得2分,有选错的得0分.小明在做多选题的第11题、第12题时通常有两种策略:
策略 为避免选错只选出一个最有把握的选项.这种策略每个题耗时约3min.
为避免选错只选出一个最有把握的选项.这种策略每个题耗时约3min.
策略 选出自己认为正确的全部选项.这种策略每个题耗时约6min.
选出自己认为正确的全部选项.这种策略每个题耗时约6min.
某次数学考试临近,小明通过前期大量模拟训练得出了两种策略下第11题和第12题的作答情况如下:
第11题:如果采用策略 ,选对的概率为0.8,采用策略
,选对的概率为0.8,采用策略 ,部分选对的概率为0.5,全部选对的概率为0.4.
,部分选对的概率为0.5,全部选对的概率为0.4.
第12题:如果采用策略 ,选对的概率为0.7,采用策略
,选对的概率为0.7,采用策略 ,部分选对的概率为0.6,全部选对的概率为0.3.
,部分选对的概率为0.6,全部选对的概率为0.3.
如果这两题总用时超过10min,其他题目会因为时间紧张少得2分.假设小明作答两题的结果互不影响.
(1)若小明同学此次考试中决定第11题采用策略 、第12题采用策略
、第12题采用策略 ,设此次考试他第11题和第12题总得分为
,设此次考试他第11题和第12题总得分为 ,求
,求 的分布列.
的分布列.
(2)小明考前设计了以下两种方案:
方案1:第11题采用策略 ,第12题采用策略
,第12题采用策略 ;
;
方案2:第11题和第12题均采用策略 .
.
如果你是小明的指导老师,从整张试卷尽可能得分更高的角度出发,你赞成他的哪种方案?并说明理由.
策略
 为避免选错只选出一个最有把握的选项.这种策略每个题耗时约3min.
为避免选错只选出一个最有把握的选项.这种策略每个题耗时约3min.策略
 选出自己认为正确的全部选项.这种策略每个题耗时约6min.
选出自己认为正确的全部选项.这种策略每个题耗时约6min.某次数学考试临近,小明通过前期大量模拟训练得出了两种策略下第11题和第12题的作答情况如下:
第11题:如果采用策略
 ,选对的概率为0.8,采用策略
,选对的概率为0.8,采用策略 ,部分选对的概率为0.5,全部选对的概率为0.4.
,部分选对的概率为0.5,全部选对的概率为0.4.第12题:如果采用策略
 ,选对的概率为0.7,采用策略
,选对的概率为0.7,采用策略 ,部分选对的概率为0.6,全部选对的概率为0.3.
,部分选对的概率为0.6,全部选对的概率为0.3.如果这两题总用时超过10min,其他题目会因为时间紧张少得2分.假设小明作答两题的结果互不影响.
(1)若小明同学此次考试中决定第11题采用策略
 、第12题采用策略
、第12题采用策略 ,设此次考试他第11题和第12题总得分为
,设此次考试他第11题和第12题总得分为 ,求
,求 的分布列.
的分布列.(2)小明考前设计了以下两种方案:
方案1:第11题采用策略
 ,第12题采用策略
,第12题采用策略 ;
;方案2:第11题和第12题均采用策略
 .
.如果你是小明的指导老师,从整张试卷尽可能得分更高的角度出发,你赞成他的哪种方案?并说明理由.
您最近一年使用:0次
2022-08-12更新
|
710次组卷
|
9卷引用:黑龙江省哈尔滨德强学校2022-2023学年高二下学期3月月考数学试题A
黑龙江省哈尔滨德强学校2022-2023学年高二下学期3月月考数学试题A山东省济南市2020-2021学年高二下学期期末数学试题山东省菏泽第一中学2021-2022学年高二下学期第三次阶段考试(月考)数学试题2023版 北师大版(2019) 选修第一册 突围者 第六章 全章综合检测2023版 北师大版(2019) 选修第一册 突围者 第六章 全章综合检测(已下线)第09讲 高考中的概率与统计 (精讲)-2福建师范大学附属中学2023届高三上学期第一次月考数学试题湖北省鄂州市第二中学2022-2023学年高三下学期2月月考数学试题山东省新高考联合质量测评2022-2023学年高二下学期3月月考数学试题
名校
解题方法
10 . 某光伏企业投资 万元用于太阳能发电项目,
万元用于太阳能发电项目,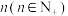 年内的总维修保养费用为
年内的总维修保养费用为 万元,该项目每年可给公司带来
万元,该项目每年可给公司带来 万元的收入.假设到第
万元的收入.假设到第 年年底,该项目的纯利润为
年年底,该项目的纯利润为 万元.(纯利润
万元.(纯利润 累计收入
累计收入 总维修保养费用
总维修保养费用 投资成本)
投资成本)
(1)写出纯利润 的表达式,并求该项目从第几年起开始盈利.
的表达式,并求该项目从第几年起开始盈利.
(2)若干年后,该公司为了投资新项目,决定转让该项目,现有以下两种处理方案:
①年平均利润最大时,以 万元转让该项目;
万元转让该项目;
②纯利润最大时,以 万元转让该项目.
万元转让该项目.
你认为以上哪种方案最有利于该公司的发展?请说明理由.
 万元用于太阳能发电项目,
万元用于太阳能发电项目,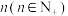 年内的总维修保养费用为
年内的总维修保养费用为 万元,该项目每年可给公司带来
万元,该项目每年可给公司带来 万元的收入.假设到第
万元的收入.假设到第 年年底,该项目的纯利润为
年年底,该项目的纯利润为 万元.(纯利润
万元.(纯利润 累计收入
累计收入 总维修保养费用
总维修保养费用 投资成本)
投资成本)(1)写出纯利润
 的表达式,并求该项目从第几年起开始盈利.
的表达式,并求该项目从第几年起开始盈利.(2)若干年后,该公司为了投资新项目,决定转让该项目,现有以下两种处理方案:
①年平均利润最大时,以
 万元转让该项目;
万元转让该项目;②纯利润最大时,以
 万元转让该项目.
万元转让该项目.你认为以上哪种方案最有利于该公司的发展?请说明理由.
您最近一年使用:0次
2022-08-15更新
|
2518次组卷
|
32卷引用:黑龙江省哈尔滨德强高中2022-2023学年高一10月月考数学试题
黑龙江省哈尔滨德强高中2022-2023学年高一10月月考数学试题福建省泉州第五中学2020-2021学年高一上学期期中考试数学试题四川省成都市四川大学附属中学2021-2022学年高一上学期期中考试数学试题福建省莆田市莆田第四中学2021-2022学年高一上学期数学期中考试题四川省凉山州宁南中学2021-2022学年高一下学期开学考试数学试题2023版 湘教版(2019) 必修第一册 突围者 第2章 第三节 课时2 一元二次不等式的应用苏教版(2019) 必修第一册 突围者 第3章 第三节 从函数观点看一元二次方程和一元二次不等式(已下线)专题02 等式与不等式(讲义)-2湖南省长沙市南雅中学2022-2023学年高一上学期第一次月考数学试题广东省佛山市石门高级中学2022-2023学年高一上学期第一次统测数学试题福建省福州格致中学2022-2023学年高一上学期期中线上适应性训练数学试题湖北省孝感市重点高中教科研协作体2022-2023学年高一上学期期中联考数学试题江西省赣州教育发展联盟2022-2023学年高一上学期第9次联考数学试题辽宁省沈阳市东北育才学校高中部2022-2023学年高一上学期开学摸底考试数学试题第3章 不等式 单元综合测试卷-2022-2023学年高一数学新教材同步配套教学讲义(苏教版2019必修第一册)(已下线)3.3.2.2 从函数观点看一元二次不等式-2022-2023学年高一数学《基础·重点·难点 》全面题型高分突破(苏教版2019必修第一册)宁夏银川市第六中学2023-2024学年高一上学期第一次月考数学试题广西南宁市第三十六中学衡阳校区2023-2024学年高一上学期9月月考数学试题吉林省长春市第二中学2023-2024学年高一上学期10月月考数学试题福建省厦门市厦门大学附属科技中学2023-2024学年高一上学期10月月考数学试题上海市复兴高级中学2023-2024学年高一上学期10月月考数学试题广东省深圳市龙岗区龙城高级中学2023-2024学年高一上学期10月段考数学试题河南省南阳市第八中学校等六校2023-2024学年高一上学期第一次联考数学试题 云南省昆明市第三中学2022-2023学年高一上学期第一册综合测试数学试题湖南省株洲市九方中学2023-2024学年高一上学期9月月考数学试题B卷河南省郑州市第十一中学2023-2024学年高一上学期10月月考数学试题江苏省苏州大学附属中学2023-2024学年高一上学期10月月考数学试题山东省青岛平度市第一中学2023-2024学年高一上学期10月月考数学试题(已下线)北京市第四中学2024届高三上学期10月月考数学试题变式题16-21湖南省张家界市慈利县第一中学2023-2024学年高一上学期第一次月考数学试题广东省汕头市龙湖区汕头经济特区林百欣中学2023-2024学年高一上学期期末数学模拟试卷(已下线)第2章 等式与不等式-【高中数学课堂】单元测试能力卷(人教B版2019)















