1 . ”鸡兔同笼”我国隋朝时期数学著作《孙子算经》中的一个有趣题目:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”
(1)求出鸡、兔各几只?
(2)根据提示,设计这类问题的通用解法,并画出算法的程序框图.
解:设有 只鸡,
只鸡, 只兔,总头数为
只兔,总头数为 ,总脚数为
,总脚数为 ,则
,则 ,解方程得:
,解方程得: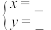
用数学语言:
第一步:输入______,______;
第二步:计算鸡的只数______;
第三步:计算兔的只数______;
第四步:输出______.
(1)求出鸡、兔各几只?
(2)根据提示,设计这类问题的通用解法,并画出算法的程序框图.
解:设有
 只鸡,
只鸡, 只兔,总头数为
只兔,总头数为 ,总脚数为
,总脚数为 ,则
,则 ,解方程得:
,解方程得: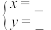
用数学语言:
第一步:输入______,______;
第二步:计算鸡的只数______;
第三步:计算兔的只数______;
第四步:输出______.

您最近一年使用:0次
2 . (1)解关于 的不等式
的不等式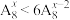 ;
;
(2)解不等式: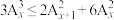 .
.
 的不等式
的不等式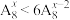 ;
;(2)解不等式:
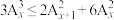 .
.
您最近一年使用:0次
2024-04-22更新
|
955次组卷
|
3卷引用:6.2.1排列-6.2.2排列数——课时作业(巩固版)
(已下线)6.2.1排列-6.2.2排列数——课时作业(巩固版)江苏省苏州青云实验中学2023-2024学年高二下学期3月月考数学试题浙江省金华市曙光学校2023-2024学年高二下学期4月月考数学试题
3 . 求关于 的方程组
的方程组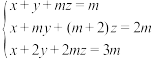 ,有唯一解的条件,并求在此条件下该方程组的解.
,有唯一解的条件,并求在此条件下该方程组的解.
 的方程组
的方程组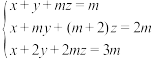 ,有唯一解的条件,并求在此条件下该方程组的解.
,有唯一解的条件,并求在此条件下该方程组的解.
您最近一年使用:0次
4 . 求关于 的方程组:
的方程组: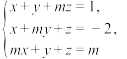 有唯一解的条件,并求在此条件下该方程组的解.
有唯一解的条件,并求在此条件下该方程组的解.
 的方程组:
的方程组: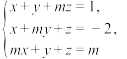 有唯一解的条件,并求在此条件下该方程组的解.
有唯一解的条件,并求在此条件下该方程组的解.
您最近一年使用:0次
5 . 判断(正确的打“√”,错误的打“×”)
(1)二元一次不等式x+y>2的解有无数多个.( )
(2)二元一次不等式(组)的解集可以看成直角坐标系内的点构成的集合.( )
(3)二元一次不等式组中的每个不等式都必须是二元一次不等式.( )
(1)二元一次不等式x+y>2的解有无数多个.
(2)二元一次不等式(组)的解集可以看成直角坐标系内的点构成的集合.
(3)二元一次不等式组中的每个不等式都必须是二元一次不等式.
您最近一年使用:0次
6 . 已知一次函数f(x)=ax-2.
(1)当a=3时,解不等式|f(x)|<4;
(2)解关于x的不等式|f(x)|<4;
(3)若关于x的不等式|f(x)|≤3对任意x∈[0,1]恒成立,求实数a的取值范围.
(1)当a=3时,解不等式|f(x)|<4;
(2)解关于x的不等式|f(x)|<4;
(3)若关于x的不等式|f(x)|≤3对任意x∈[0,1]恒成立,求实数a的取值范围.
您最近一年使用:0次
7 . 解方程组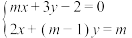 ,并求使得
,并求使得 的实数
的实数 的取值范围.
的取值范围.
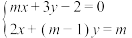 ,并求使得
,并求使得 的实数
的实数 的取值范围.
的取值范围.
您最近一年使用:0次
8 . 已知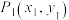 ,
,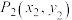 是直线
是直线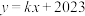 (
( 为常数)上两个不同的点,则关于
为常数)上两个不同的点,则关于 和
和 的方程组
的方程组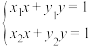 的解的情况,下列说法正确的是( )
的解的情况,下列说法正确的是( )
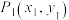 ,
,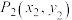 是直线
是直线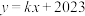 (
( 为常数)上两个不同的点,则关于
为常数)上两个不同的点,则关于 和
和 的方程组
的方程组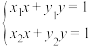 的解的情况,下列说法正确的是( )
的解的情况,下列说法正确的是( )A.无论 , , , , 如何,总是无解 如何,总是无解 |
B.无论 , , , , 如何,总有唯一解 如何,总有唯一解 |
C.存在 , , , , ,使 ,使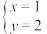 是方程组的一组解 是方程组的一组解 |
D.存在 , , , , ,使之有无穷多解 ,使之有无穷多解 |
您最近一年使用:0次
名校
9 . 已知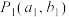 与
与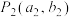 是直线
是直线 (k为常数)上两个不同的点,则关于x和y的方程组
(k为常数)上两个不同的点,则关于x和y的方程组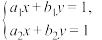 的解的情况是( )
的解的情况是( )
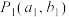 与
与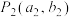 是直线
是直线 (k为常数)上两个不同的点,则关于x和y的方程组
(k为常数)上两个不同的点,则关于x和y的方程组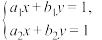 的解的情况是( )
的解的情况是( )A.无论k、 、 、 如何,总是无解 如何,总是无解 |
B.无论k、 、 、 如何,总有唯一解; 如何,总有唯一解; |
C.存在k、 、 、 ,使之恰有两解 ,使之恰有两解 |
D.存在k、 、 、 ,使之有无穷多解 ,使之有无穷多解 |
您最近一年使用:0次
2023-07-21更新
|
551次组卷
|
38卷引用:人教A版(2019) 选择性必修第一册 过关斩将 第二章 直线和圆的方程 专题强化练4 直线方程及其应用
人教A版(2019) 选择性必修第一册 过关斩将 第二章 直线和圆的方程 专题强化练4 直线方程及其应用(已下线)2.3直线的交点坐标与距离公式C卷上海市曹杨二中2018-2019学年高二下学期期中数学试题上海交通大学附属中学2019-2020学年高二上学期期中数学试题上海市川沙中学2018-2019学年高二上学期期中数学试题(已下线)上海市华东师范大学第二附属中学2016-2017学年高二上学期第一次月考数学试题2上海市复旦大学附属中学2016-2017学年高二上学期期中数学试题人教B版(2019) 选择性必修第一册 必杀技 第二章 平面解析几何 素养检测上海市徐汇区2020-2021学年高二上学期期中数学试题上海市大同中学2020-2021学年高二上学期期中数学试题上海市奉城高级中学2020-2021学年高二上学期期中数学试题上海外国语大学附属浦东外国语学校2020-2021学年高二上学期第二次检测数学试题上海市致远高级中学2020-2021学年高二上学期期末数学试题(已下线)1.4 两条直线的交点-2021-2022学年高二数学链接教材精准变式练(苏教版2019选择性必修第一册)(已下线)第1章《直线与方程》 培优测试卷(二)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)浙江省温州市瑞安中学2020-2021学年高二上学期期中数学试题苏教版(2019) 选修第一册 必杀技 第一章 素养检测(已下线)第04讲 两条直线的交点-【帮课堂】2021-2022学年高二数学同步精品讲义(苏教版2019选择性必修第一册)(已下线)第二章 直线和圆的方程(培优必刷卷)-2021-2022学年高二数学上学期同步课堂单元测试(人教A版2019选择性必修第一册)(已下线)专题04 直线和圆的方程-直线方程及其应用-2021-2022学年高二数学同步练习和分类专题教案(人教A版2019选择性必修第一册)福建省泉州科技中学2021-2022学年高二上学期第一次月考数学试题江西省新余市第一中学2022-2023学年高二上学期开学考试数学试题河北省邯郸市魏县2022-2023学年高二上学期期末考试数学试题上海市格致中学2022-2023学年高二下学期期末数学试题(已下线)第05讲 倾斜角与斜率(7大考点)(已下线)上海市高二数学下学期期末模拟试卷02--高二期末考点大串讲(沪教版2020选修)江苏省苏州市实验中学2019-2020学年高一下学期期初4月学情调研数学试题沪教版(上海) 高三年级 新高考辅导与训练 第二部分 走近高考 第十章 坐标平面上的直线与线性规划高考题选湖北省武汉市武昌实验中学2019-2020学年高一下学期5月月考数学试题(已下线)考点31 平面向量的线性运算-备战2021年高考数学经典小题考前必刷(新高考地区专用)(已下线)考点17 平面向量的概念及其线性运算-备战2022年高考数学(文)一轮复习考点帮上海市七宝中学2022届高三冲刺模拟卷二数学试题(已下线)第31练 直线方程江西省宜春市万载中学2021-2022学年高一下学期5月月考数学(理)试题辽宁省沈阳市东北育才学校2016-2017学年高三上学期期中考试数学试题(理科)(已下线)第10讲 直线的交点坐标与距离公式(1)(已下线)专题16 解析几何选择题(理科)-1(已下线)专题15 解析几何选择题(文科)-1
21-22高二·全国·课后作业
10 . 观察实际情景,提出并分析问题
(1)实际情景
动物生产的经济效益主要取决于饲料,饲料品质的好坏,成本的高低直接影响动物生产的经济效益.而饲料配方是配合饲料生产的核心,要优化配方设计,必须同时解决以下三个问题:①营养需要问题,由营养学家研究修改制定,满足营养标准;②合理组合原料,不同原料的合理搭配,才能满足动物生长需要;③价格最低.
(2)提出问题
猫是大家比较喜欢养的宠物,某款宠物猫食物,含甲、乙、丙三原料,其粗脂肪、粗灰分含量及成本如下表:
现在用甲、乙、丙三种食物配成100kg混合食物,并使混合食物内至少含有56000单位粗脂肪和63000单位粗灰分,问:分别用甲、乙、丙三种食物各多少kg,才能使这100kg混合食物的成本最低?其最低成本为多少元?
(3)分析问题
根据问题的特征,可选择线性规划结合几何法求最值来处理上述问题.
2.分析数据
设用甲种食物 ,乙种食物
,乙种食物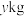 ,根据题设可得关于
,根据题设可得关于 的不等式组及成本,成本的最小值即为代数式的最小值.
的不等式组及成本,成本的最小值即为代数式的最小值.
3.建立模型
设用甲种食物 ,乙种食物
,乙种食物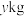 ,则可得
,则可得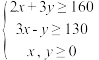 ,求
,求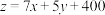 ,画出不等式组表示的平面区域,数形结合即可求出最小值.
,画出不等式组表示的平面区域,数形结合即可求出最小值.
4.问题解决
设用甲种食物 ,乙种食物
,乙种食物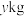 ,丙种食物
,丙种食物 ,混合食物的成本为
,混合食物的成本为 元.
元.
则 ,即
,即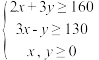 ,
,
且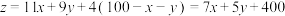 ,可化为
,可化为 ,
,
画出不等式组表示的平面区域,如图阴影部分,
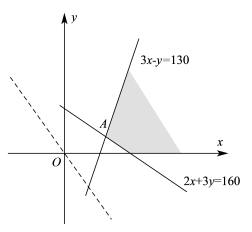
观察图形可知,当直线 过点
过点 时,
时, 取得最小值,
取得最小值,
联立方程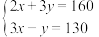 ,解得
,解得 ,即
,即
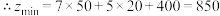 .
.
即用甲种食物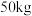 ,乙种食物
,乙种食物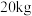 ,丙种食物
,丙种食物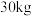 ,混合食物的成本最小为
,混合食物的成本最小为 元.
元.
5.问题拓展
如果宠物猫食物含有更多的成分,比如还有氨基酸、牛磺酸等,那么又控制成本?请收集此类问题并做深入研究.
(1)实际情景
动物生产的经济效益主要取决于饲料,饲料品质的好坏,成本的高低直接影响动物生产的经济效益.而饲料配方是配合饲料生产的核心,要优化配方设计,必须同时解决以下三个问题:①营养需要问题,由营养学家研究修改制定,满足营养标准;②合理组合原料,不同原料的合理搭配,才能满足动物生长需要;③价格最低.
(2)提出问题
猫是大家比较喜欢养的宠物,某款宠物猫食物,含甲、乙、丙三原料,其粗脂肪、粗灰分含量及成本如下表:
甲 | 乙 | 丙 | |
粗脂肪(单位/kg) | 600 | 700 | 400 |
粗灰分(单位/kg) | 800 | 400 | 500 |
成本(元/kg) | 11 | 9 | 4 |
(3)分析问题
根据问题的特征,可选择线性规划结合几何法求最值来处理上述问题.
2.分析数据
设用甲种食物
 ,乙种食物
,乙种食物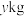 ,根据题设可得关于
,根据题设可得关于 的不等式组及成本,成本的最小值即为代数式的最小值.
的不等式组及成本,成本的最小值即为代数式的最小值.3.建立模型
设用甲种食物
 ,乙种食物
,乙种食物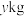 ,则可得
,则可得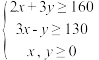 ,求
,求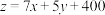 ,画出不等式组表示的平面区域,数形结合即可求出最小值.
,画出不等式组表示的平面区域,数形结合即可求出最小值.4.问题解决
设用甲种食物
 ,乙种食物
,乙种食物 ,丙种食物
,丙种食物 ,混合食物的成本为
,混合食物的成本为 元.
元.则
 ,即
,即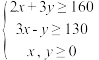 ,
,且
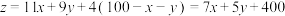 ,可化为
,可化为 ,
,画出不等式组表示的平面区域,如图阴影部分,

观察图形可知,当直线
 过点
过点 时,
时, 取得最小值,
取得最小值,联立方程
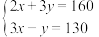 ,解得
,解得 ,即
,即
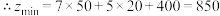 .
.即用甲种食物
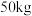 ,乙种食物
,乙种食物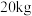 ,丙种食物
,丙种食物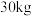 ,混合食物的成本最小为
,混合食物的成本最小为 元.
元.5.问题拓展
如果宠物猫食物含有更多的成分,比如还有氨基酸、牛磺酸等,那么又控制成本?请收集此类问题并做深入研究.
您最近一年使用:0次



