名校
1 . 排序不等式:设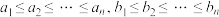 为两组实数,
为两组实数, 是
是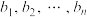 的任一排列,那么
的任一排列,那么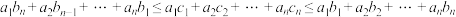 ,即“反序和≤乱序和≤顺序和”.当且仅当
,即“反序和≤乱序和≤顺序和”.当且仅当 或
或 时,反序和等于顺序和.
时,反序和等于顺序和.
(1)设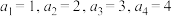 ,
,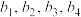 是
是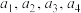 的任一排列,则乘积的值
的任一排列,则乘积的值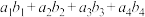 不会超过_______.
不会超过_______.
(2)设 是n个互不相同的正整数,求证:
是n个互不相同的正整数,求证: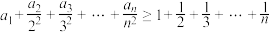
(3)有10人各拿一只水桶去接水,设水龙头注满第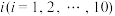 个人的水桶需要
个人的水桶需要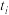 分钟,假定这些
分钟,假定这些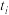 各不相同.问只有一个水龙头时,应如何安排10人的顺序,使他们等候的总时间最少?这个最少的总时间等于多少?
各不相同.问只有一个水龙头时,应如何安排10人的顺序,使他们等候的总时间最少?这个最少的总时间等于多少?
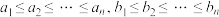 为两组实数,
为两组实数, 是
是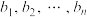 的任一排列,那么
的任一排列,那么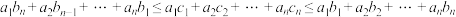 ,即“反序和≤乱序和≤顺序和”.当且仅当
,即“反序和≤乱序和≤顺序和”.当且仅当 或
或 时,反序和等于顺序和.
时,反序和等于顺序和.(1)设
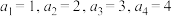 ,
,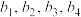 是
是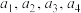 的任一排列,则乘积的值
的任一排列,则乘积的值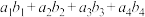 不会超过_______.
不会超过_______.(2)设
 是n个互不相同的正整数,求证:
是n个互不相同的正整数,求证: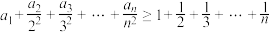
(3)有10人各拿一只水桶去接水,设水龙头注满第
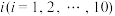 个人的水桶需要
个人的水桶需要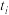 分钟,假定这些
分钟,假定这些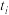 各不相同.问只有一个水龙头时,应如何安排10人的顺序,使他们等候的总时间最少?这个最少的总时间等于多少?
各不相同.问只有一个水龙头时,应如何安排10人的顺序,使他们等候的总时间最少?这个最少的总时间等于多少?
您最近一年使用:0次
名校
2 . 关于 的不等式
的不等式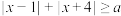 的解集为
的解集为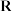 ,则实数
,则实数 的取值范围是
的取值范围是______ .
 的不等式
的不等式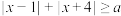 的解集为
的解集为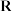 ,则实数
,则实数 的取值范围是
的取值范围是
您最近一年使用:0次
3 . (1)解关于x的不等式: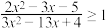 ;
;
(2)解关于x的不等式: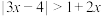 ;
;
(3)已知 ,
,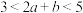 ,求
,求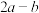 的取值范围.
的取值范围.
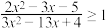 ;
;(2)解关于x的不等式:
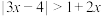 ;
;(3)已知
 ,
,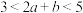 ,求
,求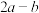 的取值范围.
的取值范围.
您最近一年使用:0次
名校
4 . 已知 ,
, ,关于x的不等式
,关于x的不等式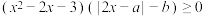 在
在 上恒成立,则( )
上恒成立,则( )
 ,
, ,关于x的不等式
,关于x的不等式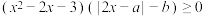 在
在 上恒成立,则( )
上恒成立,则( )A. |
B. |
C.不等式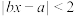 的解集为 的解集为 |
D.不等式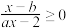 的解集为 的解集为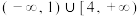 |
您最近一年使用:0次
2024高一上·江苏·专题练习
5 . 已知函数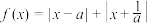 .若存在
.若存在 ,使得
,使得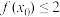 成立,则
成立,则 的取值范围是
的取值范围是___ .
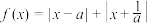 .若存在
.若存在 ,使得
,使得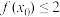 成立,则
成立,则 的取值范围是
的取值范围是
您最近一年使用:0次
名校
6 . 求下列不等式的解集(直接写结果即可不需要过程)
(1)
(2)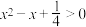
(3)
(4)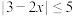
(1)

(2)
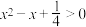
(3)

(4)
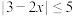
您最近一年使用:0次
名校
7 . 定义:如果在平面直角坐标系中,点 的坐标分别为
的坐标分别为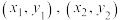 ,那么称
,那么称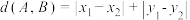 为
为 两点间的曼哈顿距离.
两点间的曼哈顿距离.
(1)已知点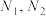 分别在直线
分别在直线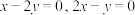 上,点
上,点 与点
与点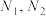 的曼哈顿距离分别为
的曼哈顿距离分别为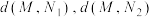 ,求
,求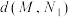 和
和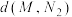 的最小值;
的最小值;
(2)已知点 是直线
是直线 上的动点,点
上的动点,点 与点
与点 的曼哈顿距离
的曼哈顿距离 的最小值记为
的最小值记为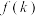 ,求
,求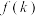 的最大值;
的最大值;
(3)已知点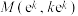 ,点
,点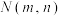 (
(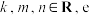 是自然对数的底),当
是自然对数的底),当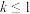 时,
时, 的最大值为
的最大值为 ,求
,求 的最小值.(注:函数
的最小值.(注:函数 在
在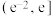 内单调递增,
内单调递增, 在
在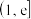 内单调递减)
内单调递减)
 的坐标分别为
的坐标分别为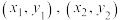 ,那么称
,那么称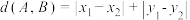 为
为 两点间的曼哈顿距离.
两点间的曼哈顿距离.(1)已知点
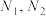 分别在直线
分别在直线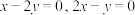 上,点
上,点 与点
与点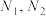 的曼哈顿距离分别为
的曼哈顿距离分别为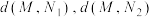 ,求
,求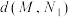 和
和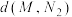 的最小值;
的最小值;(2)已知点
 是直线
是直线 上的动点,点
上的动点,点 与点
与点 的曼哈顿距离
的曼哈顿距离 的最小值记为
的最小值记为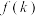 ,求
,求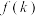 的最大值;
的最大值;(3)已知点
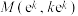 ,点
,点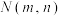 (
(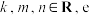 是自然对数的底),当
是自然对数的底),当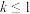 时,
时, 的最大值为
的最大值为 ,求
,求 的最小值.(注:函数
的最小值.(注:函数 在
在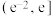 内单调递增,
内单调递增, 在
在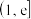 内单调递减)
内单调递减)
您最近一年使用:0次
名校
8 . 已知 :
: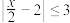 ,
, :
: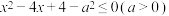 ,
, 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
 :
: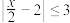 ,
, :
: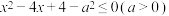 ,
, 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
9 . 若不等式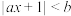 的解集为
的解集为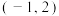 ,则实数a的取值集合为
,则实数a的取值集合为______
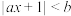 的解集为
的解集为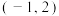 ,则实数a的取值集合为
,则实数a的取值集合为
您最近一年使用:0次
10 . 已知函数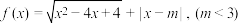 的最小值为
的最小值为 .
.
(1)求实数 的值;
的值;
(2)若正实数 满足
满足 , 证明:
, 证明: 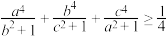 .
.
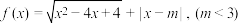 的最小值为
的最小值为 .
.(1)求实数
 的值;
的值;(2)若正实数
 满足
满足 , 证明:
, 证明: 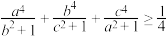 .
.
您最近一年使用:0次



