1 . 工厂需要围建一个面积为512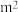 的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁.我们知道,砌起的新墙的总长度y(单位:m)是利用原有墙壁长度x(单位:m)的函数.
的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁.我们知道,砌起的新墙的总长度y(单位:m)是利用原有墙壁长度x(单位:m)的函数.
(1)写出y关于x的函数解析式,并确定x的取值范围;
(2)随着x的变化,y的变化有何规律?
(3)当堆料场的长、宽比为多少时,需要砌起的新墙用的材料最省?
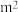 的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁.我们知道,砌起的新墙的总长度y(单位:m)是利用原有墙壁长度x(单位:m)的函数.
的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁.我们知道,砌起的新墙的总长度y(单位:m)是利用原有墙壁长度x(单位:m)的函数.(1)写出y关于x的函数解析式,并确定x的取值范围;
(2)随着x的变化,y的变化有何规律?
(3)当堆料场的长、宽比为多少时,需要砌起的新墙用的材料最省?
您最近一年使用:0次
2023-10-11更新
|
298次组卷
|
9卷引用:5.3导数在研究函数中的应用(3)
(已下线)5.3导数在研究函数中的应用(3)北师大版(2019)选择性必修第二册课本习题 习题2-7(已下线)第04讲 导数在研究函数中的应用-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)6.3利用导数解决实际问题(分层练习,5大题型)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第三册)(已下线)5.3.2课时3导数在解决实际问题中的应用 第三课 知识扩展延伸(已下线)2.7导数的应用(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第二册)(已下线)5.3.2.2函数的最大(小)值——课后作业(提升版)【导学案】7.2实际问题中的最值问题课前预习-北师大版2019选修第二册第二章导数及其应用(已下线)习题2-7
2 . 求下列函数的单调区间和极值.
(1) ;
;
(2)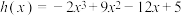 .
.
(1)
 ;
;(2)
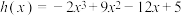 .
.
您最近一年使用:0次
21-22高二·江苏·课后作业
解题方法
3 . 试确定函数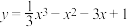 的单调区间.
的单调区间.
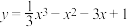 的单调区间.
的单调区间.
您最近一年使用:0次
21-22高二·江苏·课后作业
4 . 已知函数 的图象如图所示,试作出
的图象如图所示,试作出 的草图.
的草图.
 的图象如图所示,试作出
的图象如图所示,试作出 的草图.
的草图.
您最近一年使用:0次
21-22高二·江苏·课后作业
5 . 根据下列条件,大致作出函数的图象:
(1) ,
,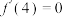 ,当
,当 时,
时,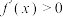 ;当
;当 时,
时,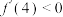 .
.
(2) ,
,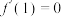 ,当
,当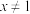 时,
时,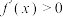 .
.
(1)
 ,
,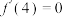 ,当
,当 时,
时,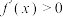 ;当
;当 时,
时,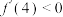 .
.(2)
 ,
,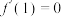 ,当
,当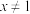 时,
时,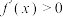 .
.
您最近一年使用:0次
21-22高二·江苏·课后作业
解题方法
6 . 求函数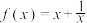 的单调区间.
的单调区间.
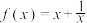 的单调区间.
的单调区间.
您最近一年使用:0次
2022-02-26更新
|
332次组卷
|
3卷引用:本章回顾5
20-21高二·全国·课后作业
7 . 求函数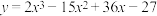 的极值点和单调区间,并画出这个函数的草图.
的极值点和单调区间,并画出这个函数的草图.
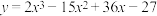 的极值点和单调区间,并画出这个函数的草图.
的极值点和单调区间,并画出这个函数的草图.
您最近一年使用:0次
名校
8 . 给定函数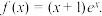
(1)判断函数 的单调性,并求出
的单调性,并求出 的极值;
的极值;
(2)画出函数 的大致图象;
的大致图象;
(3)求出方程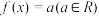 的解的个数
的解的个数
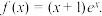
(1)判断函数
 的单调性,并求出
的单调性,并求出 的极值;
的极值;(2)画出函数
 的大致图象;
的大致图象;(3)求出方程
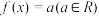 的解的个数
的解的个数
您最近一年使用:0次
2021-09-14更新
|
1603次组卷
|
11卷引用:江苏省苏州市2022-2023学年高三上学期期中数学试题
江苏省苏州市2022-2023学年高三上学期期中数学试题海南省三亚华侨学校(南新校区)2020-2021学年高二下学期3月月考数学试题天津市河北区2021-2022学年高二下学期期中数学试题山东省菏泽市巨野县实验中学2021-2022学年高二下学期第一次月考数学试题河北省承德市双滦区实验中学2022-2023学年高二下学期期中数学试题人教A版(2019)选择性必修第二册课本例题5.3 导数在研究函数中的应用云南省下关第一中学教育集团2022-2023学年高二下学期期中数学试题湖南省怀化市溆浦县玉潭高级中学2024届高三上学期第一次月考数学试题(已下线)模块四 期中重组篇(人教B版高二下云南)(已下线)【高二模块四】回归2 导数的课本典型例题和习题四川省乐山市乐山一中2023-2024学年高二下学期期中考试数学试题



