名校
解题方法
1 . 已知函数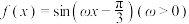 在
在 上单调递增,在
上单调递增,在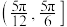 上单调递减,将函数
上单调递减,将函数 的图象向左平移
的图象向左平移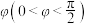 个单位长度,得到函数
个单位长度,得到函数 的图象,若函数
的图象,若函数 为偶函数,则
为偶函数,则 ( )
( )
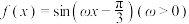 在
在 上单调递增,在
上单调递增,在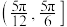 上单调递减,将函数
上单调递减,将函数 的图象向左平移
的图象向左平移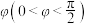 个单位长度,得到函数
个单位长度,得到函数 的图象,若函数
的图象,若函数 为偶函数,则
为偶函数,则 ( )
( )A. | B. | C. | D.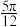 |
您最近一年使用:0次
2023-09-19更新
|
1104次组卷
|
8卷引用:吉林省敦化市实验中学校2024届高三上学期教学质量检测考试数学试题
吉林省敦化市实验中学校2024届高三上学期教学质量检测考试数学试题山东省金科大联考2023-2024学年高三上学期9月质量检测数学试题(已下线)第11讲 5.6.2 函数y=Asin(ωx+φ)的图象-【帮课堂】(已下线)5.6 函数y=Asin(ωx+φ)精练-【题型分类归纳】(人教A版2019必修第一册)河北省衡水市深州中学2024届高三上学期期末考试数学试题河北省衡水市郑口中学2024届高三第三次质量检测数学试题黑龙江省绥化市绥棱县第一中学2024届高三上学期12月月考数学试题福建省福清第一中学2024届高三上学期10月月考数学试题
2 . 已知函数 ,且
,且 图象的相邻两对称轴间的距离为
图象的相邻两对称轴间的距离为 ,则以下说法正确的是( )
,则以下说法正确的是( )
 ,且
,且 图象的相邻两对称轴间的距离为
图象的相邻两对称轴间的距离为 ,则以下说法正确的是( )
,则以下说法正确的是( )A.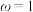 |
B.若 为偶函数,则 为偶函数,则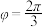 |
C.若 在区间 在区间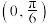 上单调递增,则 上单调递增,则 的最大值为 的最大值为 |
D.若 的一个对称中心为 的一个对称中心为 ,则 ,则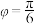 |
您最近一年使用:0次
2023-04-20更新
|
1108次组卷
|
5卷引用:吉林省长春博硕学校2022-2023学年高一下学期期中考试数学试题
名校
3 . 函数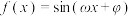 在区间
在区间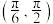 单调,其中ω为正整数,
单调,其中ω为正整数, ,且
,且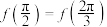 .
.
(1)求 图象的一条对称轴;
图象的一条对称轴;
(2)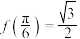 ,求
,求 .
.
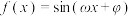 在区间
在区间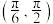 单调,其中ω为正整数,
单调,其中ω为正整数, ,且
,且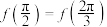 .
.(1)求
 图象的一条对称轴;
图象的一条对称轴;(2)
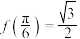 ,求
,求 .
.
您最近一年使用:0次
2023-03-25更新
|
552次组卷
|
14卷引用:2023届安徽省、云南省、吉林省、黑龙江省高三下学期2月适应性测试数学试题
2023届安徽省、云南省、吉林省、黑龙江省高三下学期2月适应性测试数学试题2023年安徽省、云南省、吉林省、黑龙江省联考数学试卷评价(已下线)2023年四省联考变试题17-22云南省2023届高三第一次高中毕业生复习统一检测数学试题山西省大同市2023届高三阶段性模拟(2月联考)数学试题(A卷)四川省广安市第二中学校2022-2023学年高一下学期第一次月考数学试题北京市第五十七中学2022-2023学年高二下学期3月月考数学试题(已下线)专题07三角函数与解三角形(解答题)广东省佛山市第一中学2022-2023学年高一下学期第一次教学质量检测数学试题重庆市第一中学教育共同体2022-2023学年高一下学期期中数学试题湖北省黄冈中学2023届高三5月二模数学试题山西省大同市第一中学校等2校2023届高三一模理科数学试题(已下线)江西省九师联盟2024届高三上学期10月联考数学试题四川省成都市温江区冠城实验学校2022-2023学年高一上学期3月月考数学试卷
名校
解题方法
4 . 如图为函数 (
( ,
, ,
, ,
, )的部分图象.
)的部分图象.
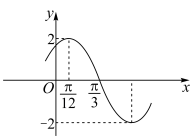
(1)求函数 的解析式;
的解析式;
(2)将函数 的图象向右平移
的图象向右平移 个单位长度,得到函数
个单位长度,得到函数 的图象,若方程
的图象,若方程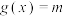 在
在 上有两个不相等的实数根,求实数
上有两个不相等的实数根,求实数 的取值范围.
的取值范围.
 (
( ,
, ,
, ,
, )的部分图象.
)的部分图象.
(1)求函数
 的解析式;
的解析式;(2)将函数
 的图象向右平移
的图象向右平移 个单位长度,得到函数
个单位长度,得到函数 的图象,若方程
的图象,若方程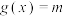 在
在 上有两个不相等的实数根,求实数
上有两个不相等的实数根,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-03-12更新
|
757次组卷
|
2卷引用:吉林省白城市通榆县毓才高级中学2022-2023学年高一下学期3月月考数学试题
名校
5 . 已知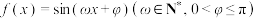 是
是 上的奇函数,且
上的奇函数,且 在区间
在区间 上是单调函数,则
上是单调函数,则 的最大值为( )
的最大值为( )
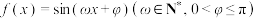 是
是 上的奇函数,且
上的奇函数,且 在区间
在区间 上是单调函数,则
上是单调函数,则 的最大值为( )
的最大值为( )| A.3 | B.4 | C.5 | D.6 |
您最近一年使用:0次
2023-03-03更新
|
888次组卷
|
3卷引用:吉林省通化市梅河口市第五中学2023届高三下学期二模考试数学试题
吉林省通化市梅河口市第五中学2023届高三下学期二模考试数学试题(已下线)第06讲 5.4.2正弦函数、余弦函数的性质(1)-【帮课堂】重庆市永川区萱花中学校2022-2023学年高一下学期3月月考数学试题
名校
6 . 已知函数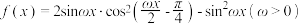 在区间[
在区间[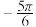 ,
,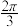 ]上是增函数,且在区间(0,π)上恰好取得一次最大值,则
]上是增函数,且在区间(0,π)上恰好取得一次最大值,则 的取值范围是
的取值范围是______ .
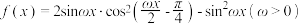 在区间[
在区间[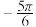 ,
,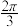 ]上是增函数,且在区间(0,π)上恰好取得一次最大值,则
]上是增函数,且在区间(0,π)上恰好取得一次最大值,则 的取值范围是
的取值范围是
您最近一年使用:0次
7 . 已知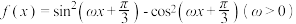 .给出下列判断,其中,判断错误的是( )
.给出下列判断,其中,判断错误的是( )
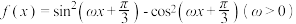 .给出下列判断,其中,判断错误的是( )
.给出下列判断,其中,判断错误的是( )A.若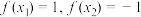 ,且 ,且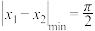 ,则 ,则 |
B.若f(x)在[0,2π]上恰有9个零点,则 的取值范围为 的取值范围为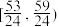 |
C.存在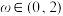 ,使得f(x)的图象向右平移 ,使得f(x)的图象向右平移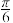 个单位长度后得到的图象关于y轴对称 个单位长度后得到的图象关于y轴对称 |
D.若f(x)在[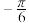 , , ]上单调递增,则的取值范围为(0, ]上单调递增,则的取值范围为(0, ]. ]. |
您最近一年使用:0次
名校
8 . 若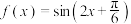 在区间
在区间 上单调递增,则实数
上单调递增,则实数 的取值范围为( )
的取值范围为( )
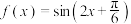 在区间
在区间 上单调递增,则实数
上单调递增,则实数 的取值范围为( )
的取值范围为( )A.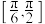 | B. | C.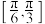 | D.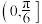 |
您最近一年使用:0次
2023-01-15更新
|
1982次组卷
|
8卷引用:吉林省长春市实验中学2022-2023学年高二下学期4月月考数学试题
名校
9 . (1)已知函数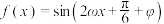 (
( ,
, )是偶函数,则
)是偶函数,则
______ ,
(2)函数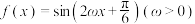 在
在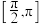 上单调递增,则
上单调递增,则 的最大值为
的最大值为______ .
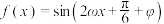 (
( ,
, )是偶函数,则
)是偶函数,则
(2)函数
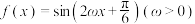 在
在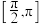 上单调递增,则
上单调递增,则 的最大值为
的最大值为
您最近一年使用:0次
名校
10 . 已知函数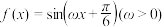 在区间
在区间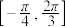 上单调递增,则
上单调递增,则 的取值范围为( )
的取值范围为( )
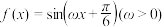 在区间
在区间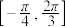 上单调递增,则
上单调递增,则 的取值范围为( )
的取值范围为( )A.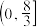 | B.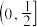 | C.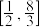 | D.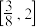 |
您最近一年使用:0次
2020-12-04更新
|
2465次组卷
|
11卷引用:吉林省田家炳高级中学2022-2023学年高一上学期期末数学试题
吉林省田家炳高级中学2022-2023学年高一上学期期末数学试题(已下线)专题04 ω 的取值范围与最值问题(2)5.7三角函数的应用浙江省湖州市南浔高级中学2023-2024学年高一上学期第三次月考数学试题【市级联考】河南省洛阳市2019届高三上学期尖子生第二次联考数学文科试题江西省宜春九中(外国语学校)2019-2020学年高一上学期第二次月考数学试题江西省南昌市八一中学2019-2020学年高一5月开学考试数学试题湖南省怀化市新博览2020-2021学年高三上学期期中联考数学试题黑龙江省实验中学2020-2021学年高三下学期2月月考试题(线上) 数学(文) 试题(已下线)第4题 正弦型函数的单调性及应用-2021年高考数学真题逐题揭秘与以例及类(新高考全国Ⅰ卷)四川省内江市威远中学校2022-2023学年高三上学期第三次月考数学(文)试题



