2024高一下·上海·专题练习
1 . 方程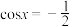 在
在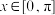 内的解为
内的解为
__ .
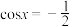 在
在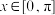 内的解为
内的解为
您最近一年使用:0次
解题方法
2 . 下列函数中,既是偶函数又在区间 上单调递增的是( )
上单调递增的是( )
 上单调递增的是( )
上单调递增的是( )A.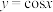 | B.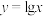 | C. | D. |
您最近一年使用:0次
解题方法
3 . 下列函数既是偶函数又在 上单调递减的是( )
上单调递减的是( )
 上单调递减的是( )
上单调递减的是( )A. | B.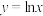 | C.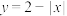 | D.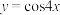 |
您最近一年使用:0次
4 . 已知函数 .
.
(1)求 的最小正周期;
的最小正周期;
(2)求 的单调递减区间.
的单调递减区间.
 .
.(1)求
 的最小正周期;
的最小正周期;(2)求
 的单调递减区间.
的单调递减区间.
您最近一年使用:0次
名校
5 . 下列函数是偶函数且在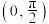 上单调递增的是( )
上单调递增的是( )
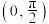 上单调递增的是( )
上单调递增的是( )A. | B.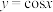 | C. | D. |
您最近一年使用:0次
名校
6 . 下列函数中,既是偶函数又在区间 上单调递增的是( )
上单调递增的是( )
 上单调递增的是( )
上单调递增的是( )A.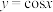 | B. | C. | D.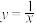 |
您最近一年使用:0次
2023-04-11更新
|
1974次组卷
|
7卷引用:浙江省杭州市杭州师范大学附属中学国际部2022-2023学年高一下学期期中数学试题
浙江省杭州市杭州师范大学附属中学国际部2022-2023学年高一下学期期中数学试题甘肃省临夏州广河中学2023-2024学年高一上学期期末模拟数学试题北京市顺义区2023届高三一模数学试题专题04基本初等函数专题03三角函数与解三角形(已下线)第02讲 函数的性质:单调性、奇偶性、周期性、对称性(十三大题型)(讲义)福建省德化第二中学2023-2024学年高二下学期7月期末考试数学试题
名校
7 . 已知函数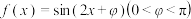 为偶函数,则( )
为偶函数,则( )
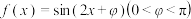 为偶函数,则( )
为偶函数,则( )A. 的图象关于直线 的图象关于直线 对称 对称 |
B. 的最小正周期是 的最小正周期是 |
C. 的图象关于点 的图象关于点 对称 对称 |
D. 在区间 在区间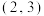 上是增函数 上是增函数 |
您最近一年使用:0次
2023-02-09更新
|
425次组卷
|
3卷引用:安徽省六安市毛坦厂中学2022-2023学年高一下学期期中考试数学试题
名校
解题方法
8 . 设函数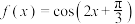 ,则( )
,则( )
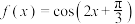 ,则( )
,则( )A. 的一个周期为 的一个周期为 |
B. 的图象关于直线 的图象关于直线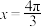 对称 对称 |
C. 的一个零点为 的一个零点为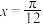 |
D. 在 在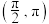 单调递减 单调递减 |
您最近一年使用:0次
9 . 有下列说法:
①函数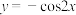 的最小正周期是
的最小正周期是 ;
;
②终边在 轴上的角的集合是
轴上的角的集合是 ;
;
③把函数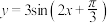 的图像上所有的点向右平移
的图像上所有的点向右平移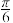 个单位长度得到函数
个单位长度得到函数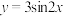 的图像;
的图像;
④函数 在
在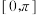 上是减函数.其中,正确的说法是
上是减函数.其中,正确的说法是__________ .(填序号)
①函数
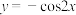 的最小正周期是
的最小正周期是 ;
;②终边在
 轴上的角的集合是
轴上的角的集合是 ;
;③把函数
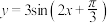 的图像上所有的点向右平移
的图像上所有的点向右平移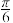 个单位长度得到函数
个单位长度得到函数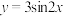 的图像;
的图像;④函数
 在
在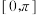 上是减函数.其中,正确的说法是
上是减函数.其中,正确的说法是
您最近一年使用:0次
名校
解题方法
10 . 学生对 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:
①原点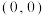 是
是 图象的对称中心;
图象的对称中心;
② 是函数
是函数 的一个周期
的一个周期
③ 在
在 上单调递增;
上单调递增;
④存在正常数 ,使
,使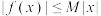 对一切实数
对一切实数 均成立.
均成立.
其中正确结论的个数是( )
 的性质进行研究,得出如下的结论:
的性质进行研究,得出如下的结论:①原点
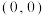 是
是 图象的对称中心;
图象的对称中心;②
 是函数
是函数 的一个周期
的一个周期③
 在
在 上单调递增;
上单调递增;④存在正常数
 ,使
,使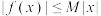 对一切实数
对一切实数 均成立.
均成立.其中正确结论的个数是( )
| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
2022-04-11更新
|
341次组卷
|
2卷引用:北京市第一六六中学2021-2022学年高一下学期期中考试数学试题



