2021·上海松江·二模
名校
解题方法
1 . 为打赢打好脱贫攻坚战,某村加大旅游业投入,准备将如图扇形空地AOB分隔成三部分建成花卉观赏区,分别种植玫瑰花、郁金香和菊花,已知扇形的半径为100米,圆心角为 ,点P在扇形的弧上,点Q在OB上,且
,点P在扇形的弧上,点Q在OB上,且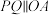 .
.
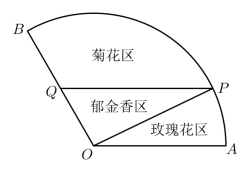
(1)当Q是OB的中点时,求PQ的长;
(2)已知种植玫瑰花、郁金香和菊花的成本分别为30元/平方米、50元/平方米、20元/平方米,要使郁金香种植区△OPQ的面积尽可能的大,求△OPQ面积的最大值,并求此时扇形区域AOB种植花卉的总成本.
 ,点P在扇形的弧上,点Q在OB上,且
,点P在扇形的弧上,点Q在OB上,且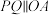 .
.
(1)当Q是OB的中点时,求PQ的长;
(2)已知种植玫瑰花、郁金香和菊花的成本分别为30元/平方米、50元/平方米、20元/平方米,要使郁金香种植区△OPQ的面积尽可能的大,求△OPQ面积的最大值,并求此时扇形区域AOB种植花卉的总成本.
您最近一年使用:0次
2022-04-15更新
|
564次组卷
|
6卷引用:一轮复习适应训练卷(9)-2022年暑假高二升高三数学一轮复习适应训练卷 全国通用
(已下线)一轮复习适应训练卷(9)-2022年暑假高二升高三数学一轮复习适应训练卷 全国通用 上海市松江区2021届高三二模数学试题(已下线)考向09 三角函数-备战2022年高考数学一轮复习考点微专题(上海专用)内蒙古霍林郭勒市第一中学2021-2022学年高一下学期第一次月考数学(理)试题(已下线)专题07 解三角形(练习)-2上海市华东师范大学第三附属中学2022-2023学年高一下学期3月月考数学试题
20-21高二·全国·单元测试
解题方法
2 . 如图,直线l为经过市中心O的一条道路,B、C是位于道路l上的两个市场,在市中心O正西方向的道路较远处分布着一些村庄,为方便村民生活,市政府决定从村庄附近的点A处修建两条道路AB、AC,l与OA的夹角为 (OA>3km,∠OAC为锐角).已知以
(OA>3km,∠OAC为锐角).已知以 的速度从O点到达B、C的时间分别为t,
的速度从O点到达B、C的时间分别为t,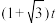 .
.
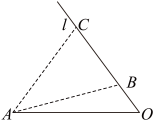
(1)当t=1时:①设计AB的长为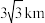 ,求此时OA的长;②修建道路AB,AC的费用均为a元/km,现需要使工程耗费最少,直接写出所需总费用的最小值.
,求此时OA的长;②修建道路AB,AC的费用均为a元/km,现需要使工程耗费最少,直接写出所需总费用的最小值.
(2)若点A与市中心O相距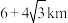 ,铺设时测量出道路AC,AB的夹角为
,铺设时测量出道路AC,AB的夹角为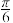 ,求时间t的值.
,求时间t的值.
 (OA>3km,∠OAC为锐角).已知以
(OA>3km,∠OAC为锐角).已知以 的速度从O点到达B、C的时间分别为t,
的速度从O点到达B、C的时间分别为t,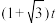 .
.
(1)当t=1时:①设计AB的长为
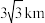 ,求此时OA的长;②修建道路AB,AC的费用均为a元/km,现需要使工程耗费最少,直接写出所需总费用的最小值.
,求此时OA的长;②修建道路AB,AC的费用均为a元/km,现需要使工程耗费最少,直接写出所需总费用的最小值.(2)若点A与市中心O相距
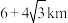 ,铺设时测量出道路AC,AB的夹角为
,铺设时测量出道路AC,AB的夹角为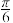 ,求时间t的值.
,求时间t的值.
您最近一年使用:0次
名校
3 . 2020年5月,我海军第35批护航编队,在亚丁湾海域开始执行护航任务,某日,护航编队旗舰“太原”舰,在 处收到某商船在航行中发出求救信号后,立即测出该商船在方位角(是从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角)为45°、距离
处收到某商船在航行中发出求救信号后,立即测出该商船在方位角(是从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角)为45°、距离 处为
处为 的
的 处,并测得该船正沿方位角为105°的方向,以
处,并测得该船正沿方位角为105°的方向,以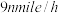 的速度航行,“太原”舰立即以
的速度航行,“太原”舰立即以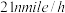 的速度航行前去营救.
的速度航行前去营救.
(1)“太原”舰最少需要多少小时才能靠近商船?
(2)在营救时间最少的前提下,“太原”舰应按照怎样的航行方向前进?
(角度精确到0.1°,参考数据: ,
, ,
,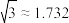 )
)
 处收到某商船在航行中发出求救信号后,立即测出该商船在方位角(是从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角)为45°、距离
处收到某商船在航行中发出求救信号后,立即测出该商船在方位角(是从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角)为45°、距离 处为
处为 的
的 处,并测得该船正沿方位角为105°的方向,以
处,并测得该船正沿方位角为105°的方向,以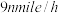 的速度航行,“太原”舰立即以
的速度航行,“太原”舰立即以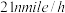 的速度航行前去营救.
的速度航行前去营救.(1)“太原”舰最少需要多少小时才能靠近商船?
(2)在营救时间最少的前提下,“太原”舰应按照怎样的航行方向前进?
(角度精确到0.1°,参考数据:
 ,
, ,
,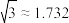 )
)
您最近一年使用:0次
2020-07-22更新
|
162次组卷
|
5卷引用:人教A版 全能练习 正余弦定理 章节能力测评(二 )
2020·江苏宿迁·一模
名校
解题方法
4 . 如图,某市管辖的海域内有一圆形离岸小岛,半径为1公里,小岛中心O到岸边AM的最近距离OA为2公里.该市规划开发小岛为旅游景区,拟在圆形小岛区域边界上某点B处新建一个浴场,在海岸上某点C处新建一家五星级酒店,在A处新建一个码头,且使得AB与AC满足垂直且相等,为方便游客,再建一条跨海高速通道OC连接酒店和小岛,设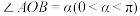 .
.
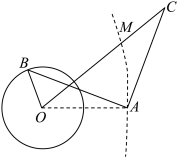
(1)设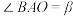 ,试将
,试将 表示成
表示成 的函数;
的函数;
(2)若OC越长,景区的辐射功能越强,问当 为何值时OC最长,并求出该最大值.
为何值时OC最长,并求出该最大值.
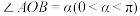 .
.
(1)设
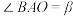 ,试将
,试将 表示成
表示成 的函数;
的函数;(2)若OC越长,景区的辐射功能越强,问当
 为何值时OC最长,并求出该最大值.
为何值时OC最长,并求出该最大值.
您最近一年使用:0次
2020-03-26更新
|
756次组卷
|
4卷引用:选择性必修第一册模块检测卷(基础过关)-2020-2021学年高二数学单元测试定心卷(人教A版2019选择性必修第一册)
(已下线)选择性必修第一册模块检测卷(基础过关)-2020-2021学年高二数学单元测试定心卷(人教A版2019选择性必修第一册)河南省郑州外国语学校2020-2021学年第一学期高二期中考试数学(理科)试题2020届江苏省宿迁市沭阳中学高三下学期百日冲刺模拟考试数学试题沪教版(2020) 必修第二册 单元训练 期末测试(B卷)
19-20高一·全国·课后作业
5 . 如图,在曲柄 绕
绕 点旋转时,活塞
点旋转时,活塞 作直线往复运动,设连杆
作直线往复运动,设连杆 长为
长为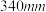 ,曲柄
,曲柄 长
长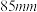 ,求曲柄
,求曲柄 从初始位置
从初始位置 按顺时针方向旋转
按顺时针方向旋转 时,活塞
时,活塞 移动的距离
移动的距离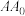 .
.

 绕
绕 点旋转时,活塞
点旋转时,活塞 作直线往复运动,设连杆
作直线往复运动,设连杆 长为
长为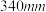 ,曲柄
,曲柄 长
长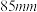 ,求曲柄
,求曲柄 从初始位置
从初始位置 按顺时针方向旋转
按顺时针方向旋转 时,活塞
时,活塞 移动的距离
移动的距离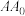 .
.
您最近一年使用:0次
2020-01-31更新
|
238次组卷
|
3卷引用:第九章 解三角形 9.2 正弦定理与余弦定理的应用
19-20高一·全国·课后作业
名校
6 . 如图所示,在某海滨城市A附近的海面出现台风活动.据监测,目前台风中心位于城市A的东偏南60°方向、距城市A300km的海面点P处,并以20km/h的速度向西偏北30°方向移动.如果台风影响的范围是以台风中心为圆心的圆形区域,半径为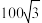 km,将问题涉及范围内的地球表面看成平面,判断城市A是否会受到上述台风的影响.如果会,求出受影响的时间;如果不会,说明理由.
km,将问题涉及范围内的地球表面看成平面,判断城市A是否会受到上述台风的影响.如果会,求出受影响的时间;如果不会,说明理由.
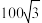 km,将问题涉及范围内的地球表面看成平面,判断城市A是否会受到上述台风的影响.如果会,求出受影响的时间;如果不会,说明理由.
km,将问题涉及范围内的地球表面看成平面,判断城市A是否会受到上述台风的影响.如果会,求出受影响的时间;如果不会,说明理由.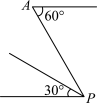
您最近一年使用:0次
2020-01-30更新
|
359次组卷
|
6卷引用:第九章 解三角形 9.2 正弦定理与余弦定理的应用
(已下线)第九章 解三角形 9.2 正弦定理与余弦定理的应用人教B版(2019) 必修第四册 逆袭之路 第九章 9.2 正弦定理与余弦定理的应用 (一)(已下线)【新教材精创】9.2 正弦定理与余弦定理的应用+导学案(2)(已下线)【新教材精创】9.2 正弦定理与余弦定理的应用(第1课时)导学案(1)辽宁省铁岭市昌图县第一高级中学2022-2023学年高一下学期6月月考数学试题人教B版(2019)必修第四册课本例题9.2 正弦定理与余弦定理的应用
7 . 在一次航模实验中,小船受到两个力的作用,已知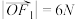 ,
, ,且
,且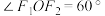 ,求合力的大小及方向.
,求合力的大小及方向.
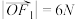 ,
, ,且
,且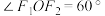 ,求合力的大小及方向.
,求合力的大小及方向.
您最近一年使用:0次
2019-11-10更新
|
113次组卷
|
2卷引用:沪教版 高二年级第一学期 领航者 第八章 附录2 向量的加减法
18-19高一下·福建·期中
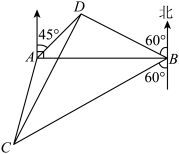
8 . 如图, ,
, 是海面上位于东西方向相海距
是海面上位于东西方向相海距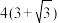 里的两个观测点,现位于
里的两个观测点,现位于 点北偏东
点北偏东 ,
, 点北偏西
点北偏西 的
的 点有一艘轮船发出求救信号,位于
点有一艘轮船发出求救信号,位于 点南偏西
点南偏西 且与
且与 点相距
点相距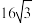 海里的
海里的 点的救援船立即前往营救,其航行速度为24海里/小时.
点的救援船立即前往营救,其航行速度为24海里/小时.
(Ⅰ)求 的长;
的长;
(Ⅱ)该救援船到达 点所需的时间.
点所需的时间.
 ,
, 是海面上位于东西方向相海距
是海面上位于东西方向相海距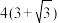 里的两个观测点,现位于
里的两个观测点,现位于 点北偏东
点北偏东 ,
, 点北偏西
点北偏西 的
的 点有一艘轮船发出求救信号,位于
点有一艘轮船发出求救信号,位于 点南偏西
点南偏西 且与
且与 点相距
点相距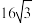 海里的
海里的 点的救援船立即前往营救,其航行速度为24海里/小时.
点的救援船立即前往营救,其航行速度为24海里/小时.
(Ⅰ)求
 的长;
的长;(Ⅱ)该救援船到达
 点所需的时间.
点所需的时间.
您最近一年使用:0次
2019-06-07更新
|
627次组卷
|
5卷引用:第19天 测量角度问题——《2019年暑假作业总动员》高二理科数学
(已下线)第19天 测量角度问题——《2019年暑假作业总动员》高二理科数学(已下线)第19天 测量角度问题——《2019年暑假作业总动员》高二文科数学【校级联考】福建省宁德市部分一级达标中学2018-2019学年高一下学期期中考试数学试题(已下线)7.5+港口水深的变化与三角函数+(基础练)-2020-2021学年高一数学十分钟同步课堂专练(苏教版2019必修第一册)浙江省金华市曙光学校2022-2023学年高一下学期3月检测数学试题
9-10高二下·河南郑州·期末
9 . 如图,金砂公园有一块边长为 的等边
的等边 的边角地,现修成草坪,图中
的边角地,现修成草坪,图中 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, 在
在 上,
上, 在
在 上.
上.
(Ⅰ)设 ,
, ,求
,求 关于
关于 的函数关系式;
的函数关系式;
(Ⅱ)如果 是灌溉水管,我们希望它最短,则
是灌溉水管,我们希望它最短,则 的位置应在哪里?请予以证明.
的位置应在哪里?请予以证明.
 的等边
的等边 的边角地,现修成草坪,图中
的边角地,现修成草坪,图中 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, 在
在 上,
上, 在
在 上.
上.(Ⅰ)设
 ,
, ,求
,求 关于
关于 的函数关系式;
的函数关系式;(Ⅱ)如果
 是灌溉水管,我们希望它最短,则
是灌溉水管,我们希望它最短,则 的位置应在哪里?请予以证明.
的位置应在哪里?请予以证明.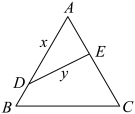
您最近一年使用:0次
2016-11-30更新
|
1499次组卷
|
5卷引用:郑州智林学校09-10学年高二下学期期末考试数学试卷(理科)
(已下线)郑州智林学校09-10学年高二下学期期末考试数学试卷(理科)(已下线)第九章 解三角形 本章小结人教B版(2019) 必修第四册 逆袭之路 第九章 解三角形 本章小结辽宁省六校2019-2020学年高一下学期期初考试数学试题人教B版(2019)必修第四册课本习题第九章本章小结



