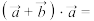1 . 若非零向量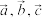 满足
满足 ,且
,且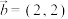 ,则能使得
,则能使得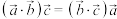 成立的一组
成立的一组 可以是
可以是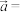
______ ,
______
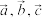 满足
满足 ,且
,且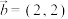 ,则能使得
,则能使得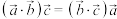 成立的一组
成立的一组 可以是
可以是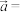

您最近一年使用:0次
2024高三·全国·专题练习
解题方法
2 . 设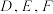 分别为
分别为 的三边
的三边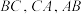 的中点,则
的中点,则 ( )
( )
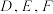 分别为
分别为 的三边
的三边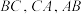 的中点,则
的中点,则 ( )
( )A.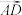 | B. | C. | D.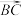 |
您最近一年使用:0次
2024·全国·模拟预测
解题方法
3 . 边长为2的等边 中,
中, 为
为 的中点,
的中点, 在边
在边 上且
上且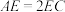 ,则
,则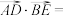
______ .
 中,
中, 为
为 的中点,
的中点, 在边
在边 上且
上且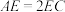 ,则
,则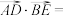
您最近一年使用:0次
名校
4 . 已知向量 共线,且
共线,且 ,则
,则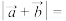
______ .
 共线,且
共线,且 ,则
,则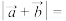
您最近一年使用:0次
2024-04-26更新
|
920次组卷
|
4卷引用:第01讲 平面向量的概念及线性运算(六大题型)(练习)
(已下线)第01讲 平面向量的概念及线性运算(六大题型)(练习)北京市十一学校2023-2024学年高一下学期期中考试数学试卷(已下线)核心考点1 平面向量的运算 B提升卷 (高一期末考试必考的10大核心考点 )山东省2023-2024学年高一下学期6月期末联考数学试卷
5 . 已知非零向量 ,
, ,满足
,满足 ,且
,且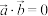 ,对任意实数
,对任意实数 ,
, ,下列结论正确的是( )
,下列结论正确的是( )
 ,
, ,满足
,满足 ,且
,且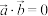 ,对任意实数
,对任意实数 ,
, ,下列结论正确的是( )
,下列结论正确的是( )A.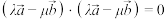 | B.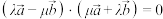 |
C.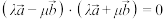 | D.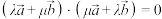 |
您最近一年使用:0次
6 . 如图是一个正六边形 ,下列说法正确的是( )
,下列说法正确的是( )
 ,下列说法正确的是( )
,下列说法正确的是( )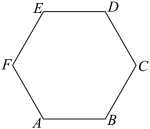
A.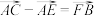 |
B.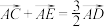 |
C. |
D.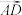 在 在 上的投影向量为 上的投影向量为 |
您最近一年使用:0次
名校
解题方法
7 . 已知正方形 的边长为1,则
的边长为1,则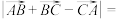 ( )
( )
 的边长为1,则
的边长为1,则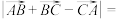 ( )
( )| A.0 | B. | C.2 | D. |
您最近一年使用:0次
2024-01-09更新
|
1924次组卷
|
5卷引用:四川省南充市2024届高三一模数学(文)试题
四川省南充市2024届高三一模数学(文)试题(已下线)考点1 平面向量的概念及线性运算 --2024届高考数学考点总动员【练】(已下线)考点27 平面向量的运算 --高考数学100个黄金考点(2025届)【讲】江西省赣州市南康中学2024届高三上学期七省联考考前数学猜题卷(三)河北省保定市高碑店市崇德实验中学2023-2024学年高一下学期3月月考数学试题
8 . 已知平面内四个不同的点 满足
满足 ,则
,则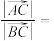 ( )
( )
 满足
满足 ,则
,则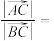 ( )
( )A. | B. | C.2 | D.3 |
您最近一年使用:0次
2023-11-09更新
|
1516次组卷
|
11卷引用:北京市朝阳区2024届高三上学期期中数学试题
北京市朝阳区2024届高三上学期期中数学试题(已下线)热点4-1 平面向量的概念、线性运算与基本定理(6题型+满分技巧+限时检测)6.2.3向量的数乘运算练习(已下线)专题02 平面向量的运算(八大考点)-【寒假自学课】(人教A版2019)(已下线)第6.2.3讲 向量的数乘运算-精讲精练宝典(已下线)6.2.3 向量的数乘运算-高频考点通关与解题策略(人教A版2019必修第二册)(已下线)6.2.3 向量的数乘运算(分层作业)-【上好课】(已下线)2.3 从速度的倍数到向量的数乘-同步精品课堂(北师大版2019必修第二册)(已下线)2.3 从速度的倍数到向量的数乘6种常见考法归类-【帮课堂】(北师大版2019必修第二册)(已下线)6.2.3 向量的数乘运算——课堂例题(已下线)第9章 平面向量 章末题型归纳总结-【帮课堂】(苏教版2019必修第二册)
解题方法
9 . 如图,在四边形ABCD中,点E,F,G,H分别为BD,AB,AC和CD的中点.求证:四边形EFGH为平行四边形.
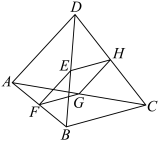
您最近一年使用:0次
2023-10-09更新
|
686次组卷
|
11卷引用:第一章 点线面位置关系 专题一 空间平行关系的判定与证明 微点1 空间直线平行的判定与证明【基础版】
(已下线)第一章 点线面位置关系 专题一 空间平行关系的判定与证明 微点1 空间直线平行的判定与证明【基础版】(已下线)考点5 平面向量的应用 --2024届高考数学考点总动员【练】北师大版(2019)必修第二册课本习题 习题2-3(已下线)专题04 平面向量的应用 (1)-【寒假自学课】(人教A版2019)(已下线)专题07 向量的应用-【寒假自学课】(苏教版2019)(已下线)专题6.5 平面向量的应用-举一反三系列(已下线)6.4.1 平面几何中的向量方法-同步精品课堂(人教A版2019必修第二册)(已下线)第09讲 6.4.1平面几何中的向量方法+6.4.2向量在物理中的应用举例-【帮课堂】(人教A版2019必修第二册)(已下线)6.4.1 平面几何中的向量方法-高频考点通关与解题策略(人教A版2019必修第二册)(已下线)6.4.1 平面几何中的向量方法——课后作业(提升版)(已下线)习题 2-3

 ,
,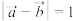 ,则
,则