解题方法
1 . 某药品可用于治疗某种疾病,经检测知每注射tml药品,从注射时间起血药浓度y(单位:ug/ml)与药品在体内时间 (单位:小时)的关系如下:
(单位:小时)的关系如下: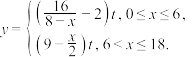 当血药浓度不低于
当血药浓度不低于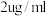 时才能起到有效治疗的作用,每次注射药品不超过
时才能起到有效治疗的作用,每次注射药品不超过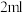 .
.
(1)若注射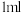 药品,求药品的有效治疗时间;
药品,求药品的有效治疗时间;
(2)若多次注射,则某一时刻体内血药浓度为每次注射后相应时刻血药浓度之和.已知病人第一次注射1ml药品,12小时之后又注射aml药品,要使随后的6小时内药品能够持续有效消疗,求 的最小值.
的最小值.
 (单位:小时)的关系如下:
(单位:小时)的关系如下: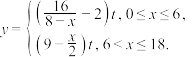 当血药浓度不低于
当血药浓度不低于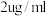 时才能起到有效治疗的作用,每次注射药品不超过
时才能起到有效治疗的作用,每次注射药品不超过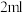 .
.(1)若注射
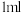 药品,求药品的有效治疗时间;
药品,求药品的有效治疗时间;(2)若多次注射,则某一时刻体内血药浓度为每次注射后相应时刻血药浓度之和.已知病人第一次注射1ml药品,12小时之后又注射aml药品,要使随后的6小时内药品能够持续有效消疗,求
 的最小值.
的最小值.
您最近一年使用:0次
名校
解题方法
2 . 已知函数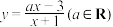 .
.
(1)若不等式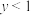 的解集为
的解集为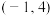 ,求
,求 的值;
的值;
(2)解关于 的不等式
的不等式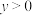 .
.
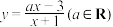 .
.(1)若不等式
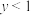 的解集为
的解集为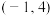 ,求
,求 的值;
的值;(2)解关于
 的不等式
的不等式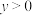 .
.
您最近一年使用:0次
2023-12-15更新
|
618次组卷
|
2卷引用:山东省淄博市桓台第一中学2023-2024学年高一上学期10月月考数学试卷
名校
解题方法
3 . 已知函数 和
和 ,定义集合
,定义集合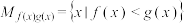 .
.
(1)设 ,求
,求 ;
;
(2)设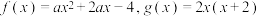 ,当
,当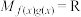 时,求
时,求 的取值范围;
的取值范围;
(3)设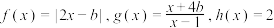 ,若
,若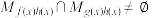 ,求
,求 的取值范围.
的取值范围.
 和
和 ,定义集合
,定义集合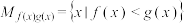 .
.(1)设
 ,求
,求 ;
;(2)设
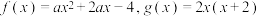 ,当
,当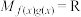 时,求
时,求 的取值范围;
的取值范围;(3)设
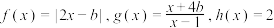 ,若
,若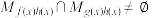 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-12-03更新
|
1258次组卷
|
3卷引用:山东省滨州市北镇中学2023-2024学年高一上学期第一届高中学科素养知识竞赛数学试题
解题方法
4 . 牧草再生力强,一年可收割多次,富含各种微量元素和维生素,因此成为饲养家畜的首选.某牧草种植公司为提高牧草的产量和质量,决定在本年度(第一年)投入80万元用于牧草的养护管理,以后每年投入金额比上一年减少 ,本年度牧草销售收入估计为60万元,由于养护管理更加精细,预计今后的牧草销售收入每年会比上一年增加
,本年度牧草销售收入估计为60万元,由于养护管理更加精细,预计今后的牧草销售收入每年会比上一年增加 .
.
(1)设n年内总投入金额为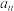 万元,牧草销售总收入为
万元,牧草销售总收入为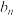 万元,求
万元,求 的表达式;
的表达式;
(2)至少经过几年,牧草销售总收入才能超过总投入? (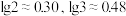 )
)
 ,本年度牧草销售收入估计为60万元,由于养护管理更加精细,预计今后的牧草销售收入每年会比上一年增加
,本年度牧草销售收入估计为60万元,由于养护管理更加精细,预计今后的牧草销售收入每年会比上一年增加 .
.(1)设n年内总投入金额为
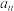 万元,牧草销售总收入为
万元,牧草销售总收入为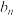 万元,求
万元,求 的表达式;
的表达式;(2)至少经过几年,牧草销售总收入才能超过总投入? (
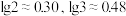 )
)
您最近一年使用:0次
2023-11-08更新
|
622次组卷
|
3卷引用:山东省烟台市2023-2024学年高三上学期期中数学试题



