名校
解题方法
1 . LED灯具有节能环保的作用,且使用寿命长.经过市场调查,可知生产某种LED灯需投入的年固定成本为4万元每生产 万件该产品,需另投入变动成本
万件该产品,需另投入变动成本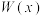 万元,在年产量不足6万件时,
万元,在年产量不足6万件时, ,在年产量不小于6万件时,
,在年产量不小于6万件时,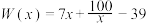 .每件产品售价为6元.假设该产品每年的销量等于当年的产量.
.每件产品售价为6元.假设该产品每年的销量等于当年的产量.
(1)写出年利润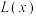 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式.(注:年利润=年销售收入-固定成本-变动成本)
(万件)的函数解析式.(注:年利润=年销售收入-固定成本-变动成本)
(2)年产量为多少万件时,年利润最大?最大年利润是多少?
 万件该产品,需另投入变动成本
万件该产品,需另投入变动成本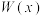 万元,在年产量不足6万件时,
万元,在年产量不足6万件时, ,在年产量不小于6万件时,
,在年产量不小于6万件时,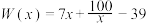 .每件产品售价为6元.假设该产品每年的销量等于当年的产量.
.每件产品售价为6元.假设该产品每年的销量等于当年的产量.(1)写出年利润
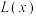 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式.(注:年利润=年销售收入-固定成本-变动成本)
(万件)的函数解析式.(注:年利润=年销售收入-固定成本-变动成本)(2)年产量为多少万件时,年利润最大?最大年利润是多少?
您最近一年使用:0次
2022-11-10更新
|
723次组卷
|
11卷引用:安徽省卓越县中联盟2022-2023学年高一上学期期中数学试题
安徽省卓越县中联盟2022-2023学年高一上学期期中数学试题湖南省部分学校2023-2024学年高一上学期10月联考数学试题湖南省郴州市第一中学2023-2024学年高一上学期10月月考数学试题安徽省合肥市庐江第五中学2023-2024学年高一上学期期中测试试题山东省枣庄市市中区辅仁高级中学2023-2024学年高一上学期11月月考数学试题湖北省武汉市洪山高级中学2024-2025学年高一上学期9月考试数学试卷山东省滕州市第二中学2024-2025学年高一上学期第一次质量检测(10月月考)数学试题安徽省合肥市合肥一六八中学2024-2025学年高一上学期第一次月考数学试题广东省佛山市第一中学2024-2025学年高一上学期10月月考数学试卷江苏省震泽中学育英学校2024-2025学年高一上学期10月月考数学试题黑龙江省黑河市嫩江市高级中学等学校(龙西北名校联盟)2024-2025学年高一上学期期中联考数学试题
名校
2 . 为提高生产效率,某公司引进新的生产线投入生产,投入生产后,除去成本,每条生产线生产的产品可获得的利润 (单位:万元)与生产线运转时间
(单位:万元)与生产线运转时间 (单位:年)满足二次函数关系:
(单位:年)满足二次函数关系: ,现在要使年平均利润最大,则每条生产线运行的时间t为( )年.
,现在要使年平均利润最大,则每条生产线运行的时间t为( )年.
 (单位:万元)与生产线运转时间
(单位:万元)与生产线运转时间 (单位:年)满足二次函数关系:
(单位:年)满足二次函数关系: ,现在要使年平均利润最大,则每条生产线运行的时间t为( )年.
,现在要使年平均利润最大,则每条生产线运行的时间t为( )年.| A.7 | B.8 | C.9 | D.10 |
您最近一年使用:0次
2024-01-12更新
|
216次组卷
|
4卷引用:上海市同济大学第二附属中学2023-2024学年高一上学期末考试数学试卷
上海市同济大学第二附属中学2023-2024学年高一上学期末考试数学试卷(已下线)专题07 基本不等式及其应用-【暑假自学课】(沪教版2020必修第一册)(已下线)2024年秋季上海高一名校分班模拟卷- 【暑假自学课】(沪教版2020必修第一册,上海专用)甘肃省天水市第一中学2024-2025学年高一上学期第一学段考试(10月)数学试题
3 . 某公司生产某种电子仪器的固定成本为2万元,每生产一台仪器需增加投入100元,公司每月生产量为x(单位:台),已知总收入R(单位:元)满足函数: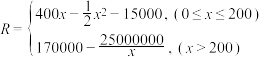
(1)将利润P表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少万元?(总收入=总成本+利润)
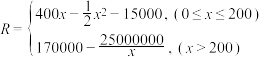
(1)将利润P表示为月产量x的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少万元?(总收入=总成本+利润)
您最近一年使用:0次
2022-01-13更新
|
293次组卷
|
4卷引用:湖南省湖湘教育三新探索协作体2021-2022学年高一上学期11月期中联考数学试题
湖南省湖湘教育三新探索协作体2021-2022学年高一上学期11月期中联考数学试题(已下线)第8章 函数应用-2021-2022学年高一数学单元过关卷(苏教版2019必修第一册)江西省上饶市广丰县第一中学2021-2022学年高一上学期期末模拟数学试题(二)(已下线)微点11 生活中的函数应用(一)【练】-高中同步微点进阶
解题方法
4 . 某大学生参加社会实践活动,对某公司 月份至
月份至 月份销售某种配件的销售量及销售单价进行了调查,销售单价
月份销售某种配件的销售量及销售单价进行了调查,销售单价 和销售量
和销售量 之间的一组数据如下表所示:
之间的一组数据如下表所示:
(1)根据 至
至 月份的数据,求出
月份的数据,求出 关于
关于 的回归直线方程;
的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过 元,则认为所得到的回归直线方程是理想的,试问
元,则认为所得到的回归直线方程是理想的,试问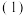 中所得到的回归直线方程是否理想?
中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从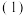 中的关系,若该种机器配件的成本是
中的关系,若该种机器配件的成本是 元
元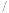 件,那么该配件的销售单价应定为多少元才能获得最大利润?
件,那么该配件的销售单价应定为多少元才能获得最大利润? 注:利润
注:利润 销售收入
销售收入 成本
成本 .
.
参考公式:回归直线方程 ,其中
,其中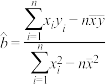 ,
,

 月份至
月份至 月份销售某种配件的销售量及销售单价进行了调查,销售单价
月份销售某种配件的销售量及销售单价进行了调查,销售单价 和销售量
和销售量 之间的一组数据如下表所示:
之间的一组数据如下表所示:| 月份 |  |  |  |  |  |  |
销售单价 元 元 | 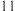 | 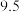 |  | 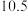 |  | 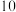 |
销售量 件 件 | 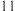 | 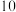 |  |  | 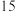 | 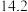 |
 至
至 月份的数据,求出
月份的数据,求出 关于
关于 的回归直线方程;
的回归直线方程;(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过
 元,则认为所得到的回归直线方程是理想的,试问
元,则认为所得到的回归直线方程是理想的,试问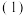 中所得到的回归直线方程是否理想?
中所得到的回归直线方程是否理想?(3)预计在今后的销售中,销售量与销售单价仍然服从
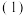 中的关系,若该种机器配件的成本是
中的关系,若该种机器配件的成本是 元
元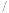 件,那么该配件的销售单价应定为多少元才能获得最大利润?
件,那么该配件的销售单价应定为多少元才能获得最大利润? 注:利润
注:利润 销售收入
销售收入 成本
成本 .
.参考公式:回归直线方程
 ,其中
,其中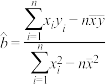 ,
,
您最近一年使用:0次
5 . 某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
预计在今后的销售中,销量与单价仍然服从这种线性相关关系,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为
(附:对于一组数据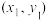 ,
,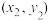 ,…,
,…, ,其回归直线
,其回归直线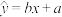 的斜率的最小二乘估计值为
的斜率的最小二乘估计值为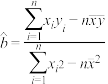 .参考数值:
.参考数值: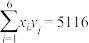 ,
,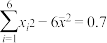 )
)
单价 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 | 100 | 94 | 93 | 90 | 85 | 78 |
(附:对于一组数据
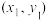 ,
,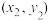 ,…,
,…, ,其回归直线
,其回归直线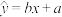 的斜率的最小二乘估计值为
的斜率的最小二乘估计值为 .参考数值:
.参考数值: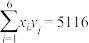 ,
,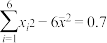 )
)| A.9.4元 | B.9.5元 | C.9.6元 | D.9.7元 |
您最近一年使用:0次
2019-02-09更新
|
288次组卷
|
2卷引用:【市级联考】福建省三明市2018-2019学年高二上学期期末质量检测数学(文)试题
名校
6 . 某商家准备促销某商品,根据市场调查,当该商品的售价定为 元时,销售量可达到
元时,销售量可达到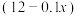 万件.已知该商品的供货价格分为固定价格和浮动价格两部分.其中固定价格为
万件.已知该商品的供货价格分为固定价格和浮动价格两部分.其中固定价格为 元/件,浮动价格(单位:元/件)与销售量(单位:万件)成反比,比例系数为
元/件,浮动价格(单位:元/件)与销售量(单位:万件)成反比,比例系数为 .假设不计其他成本,即销售每件商品的利润
.假设不计其他成本,即销售每件商品的利润 售价
售价 供货价格.
供货价格.
(1)当每件商品的售价定为 元时,求该商家所获得的总利润;
元时,求该商家所获得的总利润;
(2)该商品的售价定为多少元时,单件商品的利润最大?
 元时,销售量可达到
元时,销售量可达到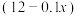 万件.已知该商品的供货价格分为固定价格和浮动价格两部分.其中固定价格为
万件.已知该商品的供货价格分为固定价格和浮动价格两部分.其中固定价格为 元/件,浮动价格(单位:元/件)与销售量(单位:万件)成反比,比例系数为
元/件,浮动价格(单位:元/件)与销售量(单位:万件)成反比,比例系数为 .假设不计其他成本,即销售每件商品的利润
.假设不计其他成本,即销售每件商品的利润 售价
售价 供货价格.
供货价格.(1)当每件商品的售价定为
 元时,求该商家所获得的总利润;
元时,求该商家所获得的总利润;(2)该商品的售价定为多少元时,单件商品的利润最大?
您最近一年使用:0次
2023-10-19更新
|
286次组卷
|
2卷引用:陕西省西安市庆安高级中学2023-2024学年高一上学期第一次月考数学试题
名校
7 . 某服装加工厂为了适应市场需求,引进某种新设备,以提高生产效率和降低生产成本.已知购买 台设备的总成本为
台设备的总成本为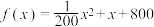 (单位:万元).若要使每台设备的平均成本最低,则应购买设备
(单位:万元).若要使每台设备的平均成本最低,则应购买设备____________ 台.
 台设备的总成本为
台设备的总成本为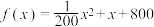 (单位:万元).若要使每台设备的平均成本最低,则应购买设备
(单位:万元).若要使每台设备的平均成本最低,则应购买设备
您最近一年使用:0次
2024-08-27更新
|
335次组卷
|
3卷引用:安徽省2023-2024学年高二下学期普通高中学业水平合格性考试仿真模拟数学试卷
名校
解题方法
8 . 某企业积极响应国家垃圾分类号召,在科研部门的支持下进行技术创新,把厨余垃圾加工处理为可重新利用的化工品,已知该企业日加工处理量x(吨)最少为70吨,最多为120吨,日加工处理总成本y(元)与日加工处理量x之间的函数关系可近似地表示为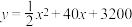 ,且每加工处理1吨厨余垃圾得到的化工产品的售价为100元.
,且每加工处理1吨厨余垃圾得到的化工产品的售价为100元.
(1)该企业日加工处理量为多少吨时,日加工处理每吨厨余垃圾的平均成本最低?此时该企业处理1吨厨余垃圾处于亏损还是盈利状态?(平均成本= )
)
(2)为了该企业可持续发展,政府决定对该企业进行财政补贴,补贴方式有两种方案
方案一:每日进行定额财政补贴,金额为2300元;
方案二:根据日加工处理量进行财政补贴,金额为40x元.
如果你是企业的决策者,为了获得每日最大利润,你会选择哪个方案进行补贴?为什么?.
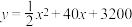 ,且每加工处理1吨厨余垃圾得到的化工产品的售价为100元.
,且每加工处理1吨厨余垃圾得到的化工产品的售价为100元.(1)该企业日加工处理量为多少吨时,日加工处理每吨厨余垃圾的平均成本最低?此时该企业处理1吨厨余垃圾处于亏损还是盈利状态?(平均成本=
 )
)(2)为了该企业可持续发展,政府决定对该企业进行财政补贴,补贴方式有两种方案
方案一:每日进行定额财政补贴,金额为2300元;
方案二:根据日加工处理量进行财政补贴,金额为40x元.
如果你是企业的决策者,为了获得每日最大利润,你会选择哪个方案进行补贴?为什么?.
您最近一年使用:0次
2023-04-01更新
|
668次组卷
|
8卷引用:江苏省苏州市常熟市2021-2022学年高一上学期期中数学试题
名校
解题方法
9 . 快递公司计划在某货运枢纽附近投资配建货物分拣中心.假定每月的土地租金成本与分拣中心到货运枢纽的距离成反比,每月的货物运输成本与分拣中心到货运枢纽的距离成正比.经测算,如果在距离货运枢纽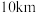 处配建分拣中心,则每月的土地租金成本和货物运输成本分别为2万元和8万元.要使得两项成本之和最小,分拣中心和货运枢纽的距离应设置为( )
处配建分拣中心,则每月的土地租金成本和货物运输成本分别为2万元和8万元.要使得两项成本之和最小,分拣中心和货运枢纽的距离应设置为( )
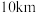 处配建分拣中心,则每月的土地租金成本和货物运输成本分别为2万元和8万元.要使得两项成本之和最小,分拣中心和货运枢纽的距离应设置为( )
处配建分拣中心,则每月的土地租金成本和货物运输成本分别为2万元和8万元.要使得两项成本之和最小,分拣中心和货运枢纽的距离应设置为( )A. | B.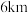 | C.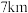 | D.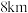 |
您最近一年使用:0次
2023-07-24更新
|
608次组卷
|
4卷引用:湖南师范大学附属中学2024届高三上学期摸底考试数学试题
湖南师范大学附属中学2024届高三上学期摸底考试数学试题(已下线)阶段性检测2.1(易)(范围:集合至复数)(已下线)2.2 基本不等式——课后作业(巩固版)黑龙江省黑河市第五中学2024-2025学年高一上学期10月月考数学试题
名校
解题方法
10 . 某医院需要建造隔离病房和药物仓库,已知建造隔离病房的所有费用 (万元)和病房与药物仓库的离
(万元)和病房与药物仓库的离 (千米)的关系为:
(千米)的关系为: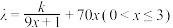 .若距离为
.若距离为 千米时,隔离病房建造费用为
千米时,隔离病房建造费用为 万元,为了方便,隔离病房与药物仓库之间还需修建一条道路,已知购置修路设备需
万元,为了方便,隔离病房与药物仓库之间还需修建一条道路,已知购置修路设备需 万元,铺设路面每千米成本为
万元,铺设路面每千米成本为 万元,设
万元,设 为建造病房与修路费用之和.
为建造病房与修路费用之和.
(1)求 的表达式:
的表达式:
(2)当隔离病房与药物仓库距离多远时,可使得总费用 最小?并求出最小值.
最小?并求出最小值.
 (万元)和病房与药物仓库的离
(万元)和病房与药物仓库的离 (千米)的关系为:
(千米)的关系为: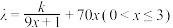 .若距离为
.若距离为 千米时,隔离病房建造费用为
千米时,隔离病房建造费用为 万元,为了方便,隔离病房与药物仓库之间还需修建一条道路,已知购置修路设备需
万元,为了方便,隔离病房与药物仓库之间还需修建一条道路,已知购置修路设备需 万元,铺设路面每千米成本为
万元,铺设路面每千米成本为 万元,设
万元,设 为建造病房与修路费用之和.
为建造病房与修路费用之和.(1)求
 的表达式:
的表达式:(2)当隔离病房与药物仓库距离多远时,可使得总费用
 最小?并求出最小值.
最小?并求出最小值.
您最近一年使用:0次
2022-10-14更新
|
909次组卷
|
7卷引用:江苏省连云港市新海高级中学2022-2023学年高一上学期10月学情调研考试数学试题



