1 . 已知正方体 的棱长为1,点
的棱长为1,点 满足
满足 (
(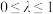 ,
,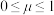 ),下列说法正确的是( )
),下列说法正确的是( )
 的棱长为1,点
的棱长为1,点 满足
满足 (
(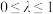 ,
,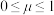 ),下列说法正确的是( )
),下列说法正确的是( )A.若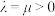 ,则 ,则 与 与 垂直 垂直 |
B.三棱锥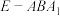 的体积恒为 的体积恒为 |
C.若 , , ,平面 ,平面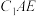 与平面 与平面 夹角的余弦值为 夹角的余弦值为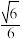 |
D.若 , , ,则点 ,则点 到平面 到平面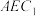 的距离为 的距离为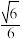 |
您最近一年使用:0次
名校
解题方法
2 . 如图,在棱长为2的正方体 中,
中, 为面
为面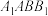 的中心,
的中心, 、
、 分别为
分别为 和
和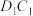 的中点,则( )
的中点,则( )
 中,
中, 为面
为面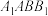 的中心,
的中心, 、
、 分别为
分别为 和
和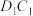 的中点,则( )
的中点,则( )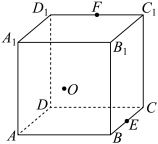
A.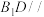 平面 平面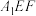 |
B.若 为 为 上的动点,则 上的动点,则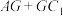 的最小值为 的最小值为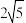 |
C.点 到直线 到直线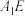 的距离为 的距离为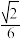 |
D.平面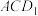 与平面 与平面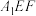 相交 相交 |
您最近一年使用:0次
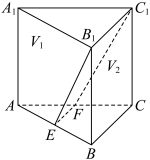
3 . 如图,三棱柱 中,
中, 分别是
分别是 的中点,平面
的中点,平面 将三棱柱分成体积为
将三棱柱分成体积为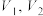 (左为
(左为 ,右为
,右为 )两部分,则
)两部分,则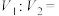 ( )
( )
 中,
中, 分别是
分别是 的中点,平面
的中点,平面 将三棱柱分成体积为
将三棱柱分成体积为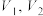 (左为
(左为 ,右为
,右为 )两部分,则
)两部分,则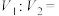 ( )
( )
A.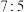 | B.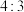 | C. | D. |
您最近一年使用:0次
2024-10-16更新
|
704次组卷
|
3卷引用:广西桂林市第十八中学2024-2025学年高二上学期开学考试数学试题
解题方法
4 . 如图,在四棱锥 中,底面
中,底面 为正方形,
为正方形, 平面
平面 ,
, 为
为 上的中点.
上的中点. 平面
平面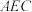 ;
;
(2)设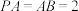 ,求三棱锥
,求三棱锥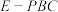 的体积.
的体积.
 中,底面
中,底面 为正方形,
为正方形, 平面
平面 ,
, 为
为 上的中点.
上的中点.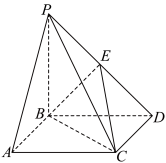
 平面
平面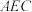 ;
;(2)设
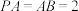 ,求三棱锥
,求三棱锥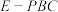 的体积.
的体积.
您最近一年使用:0次
解题方法
5 . 如图,正方体 的棱长为1,E为棱
的棱长为1,E为棱 的中点,
的中点, 为底面正方形
为底面正方形 内(含边界)的动点,则( )
内(含边界)的动点,则( )
 的棱长为1,E为棱
的棱长为1,E为棱 的中点,
的中点, 为底面正方形
为底面正方形 内(含边界)的动点,则( )
内(含边界)的动点,则( )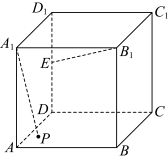
A.三棱锥 的体积为定值 的体积为定值 |
B.直线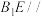 平面 平面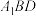 |
C.当 时,点 时,点 到平面 到平面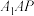 的距离为 的距离为 |
D.当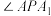 的正切值为2时,动点P的轨迹长度为 的正切值为2时,动点P的轨迹长度为 |
您最近一年使用:0次
名校
6 . 已知正三棱台 的侧面积为6,
的侧面积为6,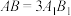 ,
,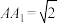 ,则
,则 与平面ABC所成角的余弦值为( )
与平面ABC所成角的余弦值为( )
 的侧面积为6,
的侧面积为6,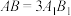 ,
,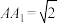 ,则
,则 与平面ABC所成角的余弦值为( )
与平面ABC所成角的余弦值为( )A. | B.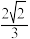 | C.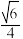 | D. |
您最近一年使用:0次
2024-10-13更新
|
476次组卷
|
2卷引用:广西南宁市2024-2025学年高三上学期普通高中毕业班摸底测试数学试题
7 . 已知正四面体的高等于球 的直径,则正四面体的体积与球
的直径,则正四面体的体积与球 的体积之比为( )
的体积之比为( )
 的直径,则正四面体的体积与球
的直径,则正四面体的体积与球 的体积之比为( )
的体积之比为( )A.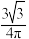 | B.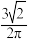 | C.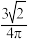 | D.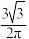 |
您最近一年使用:0次
2024-09-13更新
|
443次组卷
|
2卷引用:广西桂平市部分示范性高中2025届高三开学摸底考试数学试卷
8 . 在三棱锥中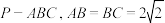 ,且
,且 .记直线
.记直线 与平面
与平面 所成角分别为
所成角分别为 ,
, ,已知
,已知 ,当三棱锥
,当三棱锥 的体积最小时,
的体积最小时, 的长为
的长为__________ .
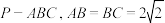 ,且
,且 .记直线
.记直线 与平面
与平面 所成角分别为
所成角分别为 ,
, ,已知
,已知 ,当三棱锥
,当三棱锥 的体积最小时,
的体积最小时, 的长为
的长为
您最近一年使用:0次
9 . 已知圆锥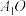 在正方体
在正方体 内,
内, ,且
,且 垂直于圆锥
垂直于圆锥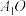 的底面,当该圆锥的底面积最大时,圆锥的体积为( )
的底面,当该圆锥的底面积最大时,圆锥的体积为( )
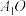 在正方体
在正方体 内,
内, ,且
,且 垂直于圆锥
垂直于圆锥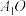 的底面,当该圆锥的底面积最大时,圆锥的体积为( )
的底面,当该圆锥的底面积最大时,圆锥的体积为( )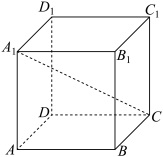
A.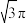 | B.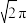 | C. | D.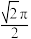 |
您最近一年使用:0次
2024-09-09更新
|
124次组卷
|
2卷引用:广西部分学校2024-2025学年高二上学期入学检测数学试题
名校
解题方法
10 . 已知正方体 的棱长为
的棱长为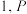 为
为 的中点.
的中点.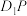
 平面
平面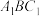 ;
;
(2)求三棱锥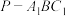 的体积.
的体积.
 的棱长为
的棱长为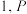 为
为 的中点.
的中点.
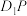
 平面
平面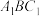 ;
;(2)求三棱锥
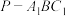 的体积.
的体积.
您最近一年使用:0次



