名校
解题方法
1 . 图,在九面体 中,平面
中,平面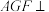 平面
平面 ,平面
,平面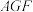
 平面
平面 ,底面
,底面 为正六边形,下列结论错误的是( )
为正六边形,下列结论错误的是( )
 中,平面
中,平面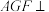 平面
平面 ,平面
,平面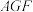
 平面
平面 ,底面
,底面 为正六边形,下列结论错误的是( )
为正六边形,下列结论错误的是( )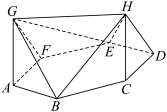
A.  平面 平面 |
B. 平面 平面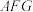 |
C.平面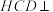 平面 平面 |
D.平面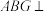 平面 平面 |
您最近一年使用:0次
2024-08-30更新
|
87次组卷
|
2卷引用:黑龙江省龙东十校2024-2025学年高二上学期开学考试数学试题
名校
解题方法
2 . 已知 ,
, ,
, 表示三条不同的直线,
表示三条不同的直线, ,
, 表示不同的平面,则( )
表示不同的平面,则( )
 ,
, ,
, 表示三条不同的直线,
表示三条不同的直线, ,
, 表示不同的平面,则( )
表示不同的平面,则( )A.若 , , ,则 ,则 |
B.若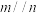 , , , ,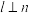 ,则 ,则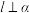 |
C.若 , , , , ,则 ,则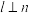 |
D.若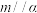 , , , ,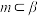 , , ,则 ,则 |
您最近一年使用:0次
2024-07-24更新
|
432次组卷
|
2卷引用:黑龙江省哈尔滨市黑龙江省实验中学2023-2024学年高一下学期期末考试数学试题
3 . 在正方体 中,
中,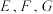 分别为
分别为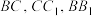 的中点,则下列结论错误的是( )
的中点,则下列结论错误的是( )
 中,
中,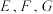 分别为
分别为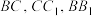 的中点,则下列结论错误的是( )
的中点,则下列结论错误的是( )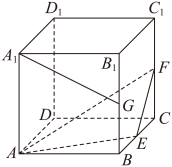
A.直线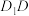 与 与 所成的角为 所成的角为 |
B.直线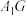 与平面 与平面 平行 平行 |
C.若正方体棱长为1,三棱锥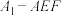 的体积是 的体积是 |
D.点 和 和 到平面 到平面 的距离之比是3∶1 的距离之比是3∶1 |
您最近一年使用:0次
名校
解题方法
4 . 已知三条不重合的直线 和平面
和平面 ,下列命题中是真命题的为( )
,下列命题中是真命题的为( )
 和平面
和平面 ,下列命题中是真命题的为( )
,下列命题中是真命题的为( )A.若直线 和平面 和平面 所成的角相等,则 所成的角相等,则   |
B.若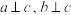 ,则 ,则   |
C.若 ,则 ,则   |
D.若 ,则 ,则   |
您最近一年使用:0次
2024-07-20更新
|
179次组卷
|
2卷引用:黑龙江省绥化市第一中学2023-2024学年高一下学期期末考试数学试卷
名校
解题方法
5 . 已知 ,
, 是空间内两条不同的直线,
是空间内两条不同的直线, ,
, ,
, 是空间内三个不同的平面,则下列说法正确的是( )
是空间内三个不同的平面,则下列说法正确的是( )
 ,
, 是空间内两条不同的直线,
是空间内两条不同的直线, ,
, ,
, 是空间内三个不同的平面,则下列说法正确的是( )
是空间内三个不同的平面,则下列说法正确的是( )A.若 , , ,则 ,则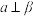 |
B.若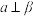 , , ,则 ,则 |
C.若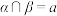 , , , ,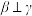 ,则 ,则 |
D.若 , ,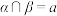 , , ,则 ,则 或 或 |
您最近一年使用:0次
2024-05-14更新
|
1559次组卷
|
4卷引用:黑龙江省大庆市实验中学实验二部2023-2024学年高三下学期阶段考试(二)数学试题
黑龙江省大庆市实验中学实验二部2023-2024学年高三下学期阶段考试(二)数学试题江西省景德镇市2024届高三第三次质检数学试题(已下线)6.5.1直线与平面垂直-【帮课堂】(北师大版2019必修第二册)(已下线)第04讲 直线、平面垂直的判定与性质(七大题型)(练习)
名校
解题方法
6 . 已知正方体 的棱
的棱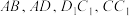 的中点分别
的中点分别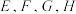 ,则下列直线中,与平面
,则下列直线中,与平面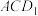 和平面
和平面 的交线平行的直线( )
的交线平行的直线( )
 的棱
的棱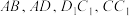 的中点分别
的中点分别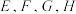 ,则下列直线中,与平面
,则下列直线中,与平面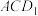 和平面
和平面 的交线平行的直线( )
的交线平行的直线( )A. | B. | C. | D.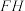 |
您最近一年使用:0次
2024-05-11更新
|
697次组卷
|
4卷引用:黑龙江省牡丹江市第一高级中学2023-2024学年高一下学期期中考试数学试题
黑龙江省牡丹江市第一高级中学2023-2024学年高一下学期期中考试数学试题河南省郑州市第一中学2023-2024学年高一下学期期中考试数学试卷(已下线)11.3.1&11.3.2 平行直线与异面直线、直线与平面平行-【帮课堂】(人教B版2019必修第四册)(已下线)暑假作业11 空间中点、线、面的平行关系-【暑假分层作业】(人教A版2019必修第二册)
名校
解题方法
7 . 如图,在空间四边形 中、点
中、点 、
、 分别是边
分别是边 、
、 上的点,
上的点, 、
、 分别是边
分别是边 、
、 上的点,
上的点,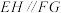 ,
,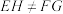 ,则下列关于直线
,则下列关于直线 ,
, 的位置关系判断正确的是( )
的位置关系判断正确的是( )
 中、点
中、点 、
、 分别是边
分别是边 、
、 上的点,
上的点, 、
、 分别是边
分别是边 、
、 上的点,
上的点,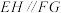 ,
,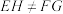 ,则下列关于直线
,则下列关于直线 ,
, 的位置关系判断正确的是( )
的位置关系判断正确的是( )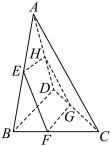
A. 与 与 互相平行; 互相平行; |
B. 与 与 是异面直线; 是异面直线; |
C. 与 与 相交,其交点在直线 相交,其交点在直线 上; 上; |
D. 与 与 相交,且交点在直线 相交,且交点在直线 上. 上. |
您最近一年使用:0次
2024-05-04更新
|
1667次组卷
|
7卷引用:黑龙江省牡丹江市第二高级中学2023-2024学年高一下学期第二次月考数学试卷
黑龙江省牡丹江市第二高级中学2023-2024学年高一下学期第二次月考数学试卷广东省广州市广州中学2023-2024学年高一下学期期中考试数学试卷(已下线)6.4.1直线与平面平行-【帮课堂】(北师大版2019必修第二册)(已下线)第8.5.2讲 直线与平面平行-同步精讲精练宝典(人教A版2019必修第二册)(已下线)11.3.1&11.3.2 平行直线与异面直线、直线与平面平行-【帮课堂】(人教B版2019必修第四册)(已下线)专题07 立体几何小题常考题型归类-期末考点大串讲(人教B版2019必修第四册)(已下线)暑假作业11 空间中点、线、面的平行关系-【暑假分层作业】(人教A版2019必修第二册)
2023高一·全国·专题练习
名校
解题方法
8 . 如图,点A,B,C,M,N为正方体的顶点或所在棱的中点,则下列各图中,不满足直线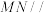 平面
平面 的是( )
的是( )
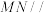 平面
平面 的是( )
的是( )A. | B. | C.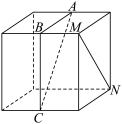 | D.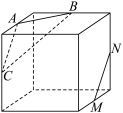 |
您最近一年使用:0次
2024-04-11更新
|
3750次组卷
|
40卷引用:黑龙江省大庆铁人中学2023-2024学年高一下学期期中数学试题
黑龙江省大庆铁人中学2023-2024学年高一下学期期中数学试题(已下线)第24讲 空间直线、平面的平行的基本概念浙江省杭州市2023届高三下学期教学质量检测(二模)数学试题(已下线)专题05 立体几何(已下线)高一数学下学期期中模拟试题03(平面向量、解三角形、复数、立体几何)江苏省苏州市第五中学2023届高三下学期4月适应性考试数学试题广东省梅州市梅江区梅州中学2023届高三冲刺热身数学试题第13章 立体几何初步(A卷·基础提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(苏教版2019必修第二册)(已下线)6.4.1直线和平面平行(课件+练习)福建省”德化一中、永安一中、漳平一中“三校协作2023届高三适应性考试数学试题(已下线)专题08 空间直线与平面的平行问题(1)-期中期末考点大串讲(已下线)重难点专题04 空间直线平面的平行-【同步题型讲义】(已下线)模块一 专题5 立体几何初步(2)(人教B)(已下线)模块一 专题5 立体几何初步(2)(北师大版)(已下线)模块一 专题3 立体几何初步(2)(人教A)(已下线)模块一 专题5 立体几何初步(2)(苏教版)福建省福州第二中学2022-2023学年高一下学期第四学段(期末)考试数学试题北京市第三十五中学2022-2023学年高二上学期期中数学试题浙江省A9协作体2023-2024学年高二上学期暑假返校联考数学试题(已下线)10.3 直线与平面间的位置关系(第1课时)(八大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020必修第三册)广东省佛山市南海区第一中学2024届高三上学期10月月考数学试题(已下线)第03讲 直线、平面平行的判定与性质(八大题型)(讲义)(已下线)第10讲 8.5.3 平面与平面平行-【帮课堂】(人教A版2019必修第二册)福建省连城县第一中学2023-2024学年高一下学期4月月考数学试题(已下线)专题18 直线与直线平行 直线与平面平行-《重难点题型·高分突破》(人教A版2019必修第二册)(已下线)8.5.2 直线与平面平行-同步题型分类归纳讲与练(人教A版2019必修第二册)福建省厦门市湖滨中学2023-2024学年高一下学期期中考试数学试题(已下线)第八章 本章综合--提炼本章思想【第二课】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)6.4.1直线与平面平行-【帮课堂】(北师大版2019必修第二册)(已下线)专题19 直线与平面的位置关系-《重难点题型·高分突破》(苏教版2019必修第二册)(已下线)专题3.5空间直线、平面的平行-重难点突破及混淆易错规避(人教A版2019必修第二册)(已下线)第六章 立体几何初步(单元测试,新题型)-同步精品课堂(北师大版2019必修第二册)(已下线)6.4 .1 直线与平面平行-同步精品课堂(北师大版2019必修第二册)重庆市第一中学校2023-2024学年高二下学期5月期中考试数学试题福建省南安市蓝园高级中学2023-2024学年高一下学期期中考试数学试题(已下线)专题04空间点、直线、平面的位置关系与空间直线、平面的平行-期末真题分类汇编(新高考专用)(已下线)专题07 立体几何小题常考题型归类-期末考点大串讲(人教B版2019必修第四册)新疆乌鲁木齐市第六十一中学2023-2024学年高一下学期期中考试数学试卷江西省上饶市第四中学2023-2024学年高一下学期6月数学测试卷(已下线)第03讲 直线、平面平行的判定与性质(八大题型)(讲义)
9 . 已知直线 ,两个不同的平面
,两个不同的平面 ,
, ,下列命题正确的是( )
,下列命题正确的是( )
 ,两个不同的平面
,两个不同的平面 ,
, ,下列命题正确的是( )
,下列命题正确的是( )A.若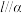 , , ,则 ,则 |
B.若 , ,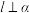 ,则 ,则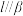 |
C.若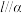 , ,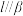 ,则 ,则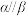 |
D.若 , ,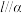 ,则 ,则 |
您最近一年使用:0次
2023-07-06更新
|
206次组卷
|
3卷引用:黑龙江省大兴安岭呼玛县高级中学2022-2023学年高二上学期开学考试数学试题
名校
解题方法
10 . 下列正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,则能满足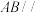 平面MNP的是( )
平面MNP的是( )
 平面MNP的是( )
平面MNP的是( )A.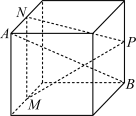 | B. |
C.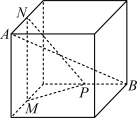 | D.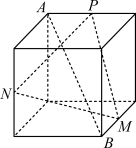 |
您最近一年使用:0次
2023-06-22更新
|
1541次组卷
|
10卷引用:黑龙江省哈尔滨市顺迈高级中学2023-2024学年高二上学期暑期作业检测数学试题
黑龙江省哈尔滨市顺迈高级中学2023-2024学年高二上学期暑期作业检测数学试题浙江省温州市2022-2023学年高一下学期期末数学试题(A卷)浙江省宁波市北仑中学2023-2024学年高二上学期期初考试数学试题(已下线)考点巩固卷17 空间中的平行与垂直(八大考点)(已下线)第09讲 空间的平行关系-【寒假预科讲义】(人教A版2019必修第二册)(已下线)第二章 立体几何中的计算 专题五 空间几何体截面问题 微点1 空间几何体截面问题(一)【基础版】(已下线)第八章 立体几何初步 单元复习提升(易错与拓展)(1)-单元速记·巧练(人教A版2019必修第二册)(已下线)8.5.2 直线与平面平行【第二练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)6.4.1直线与平面平行-【帮课堂】(北师大版2019必修第二册)(已下线)重组4 高一期末真题重组卷(浙江卷)A基础卷



