解题方法
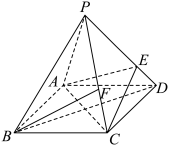
1 . 如图,在四棱锥 中,四边形
中,四边形 是正方形,
是正方形,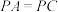 ,E为侧棱PD上的点,且
,E为侧棱PD上的点,且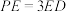 .
. ;
;
(2)在侧棱PC上是否存在一点F,使得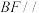 平面
平面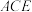 ?若存在,求
?若存在,求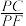 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 中,四边形
中,四边形 是正方形,
是正方形,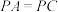 ,E为侧棱PD上的点,且
,E为侧棱PD上的点,且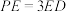 .
.
 ;
;(2)在侧棱PC上是否存在一点F,使得
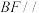 平面
平面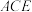 ?若存在,求
?若存在,求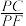 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
名校
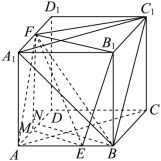
2 . 已知正方体 的棱长为3,点
的棱长为3,点 是线段
是线段 上靠近
上靠近 点的三等分点,
点的三等分点, 是
是 中点,则下列命题正确的有
中点,则下列命题正确的有______ .
①直线 与
与 所成角的正切值为
所成角的正切值为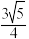 ②三棱柱
②三棱柱 外接球的半径为
外接球的半径为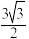
③平面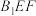 截正方体所得截面为等腰梯形 ④点
截正方体所得截面为等腰梯形 ④点 到平面
到平面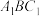 的距离为
的距离为
 的棱长为3,点
的棱长为3,点 是线段
是线段 上靠近
上靠近 点的三等分点,
点的三等分点, 是
是 中点,则下列命题正确的有
中点,则下列命题正确的有①直线
 与
与 所成角的正切值为
所成角的正切值为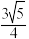 ②三棱柱
②三棱柱 外接球的半径为
外接球的半径为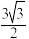
③平面
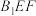 截正方体所得截面为等腰梯形 ④点
截正方体所得截面为等腰梯形 ④点 到平面
到平面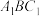 的距离为
的距离为
您最近一年使用:0次
2024-09-03更新
|
199次组卷
|
2卷引用:江苏省江安高级中学2023-2024学年高一下学期5月检测(期中模拟)数学试题
2024·全国·模拟预测
名校
解题方法
3 . 如图,四棱锥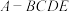 是棱长均为2的正四棱锥,三棱锥
是棱长均为2的正四棱锥,三棱锥 是正四面体,G为
是正四面体,G为 的中点,则下列结论错误的是( )
的中点,则下列结论错误的是( )
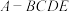 是棱长均为2的正四棱锥,三棱锥
是棱长均为2的正四棱锥,三棱锥 是正四面体,G为
是正四面体,G为 的中点,则下列结论错误的是( )
的中点,则下列结论错误的是( )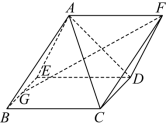
A.点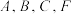 共面 共面 | B.平面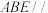 平面 平面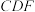 |
C. | D.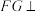 平面ACD 平面ACD |
您最近一年使用:0次
2024-09-01更新
|
382次组卷
|
10卷引用:浙江省温州中学2023-2024学年高一下学期期中考试数学试题
浙江省温州中学2023-2024学年高一下学期期中考试数学试题(已下线)专题20 平面与平面的位置关系-《重难点题型·高分突破》(苏教版2019必修第二册)(已下线)2024年普通高等学校招生全国统一考试数学文科猜题卷(一)(已下线)2024年普通高等学校招生全国统一考试数学理科猜题卷(三)(已下线)数学(广东专用01,新题型结构)(已下线)6.2 空间点、直线、平面的位置关系(高考真题素材之十年高考)(已下线)【一题多变】四点共面 向量转化新疆石河子第一中学2024届高三“天使计划”第二轮测试数学试题广东省普宁二中实验学校2023-2024学年高二下学期第三次月考数学试题河北省衡水中学2024-2025学年高二上学期第一次综合素养测评数学试题
解题方法
4 . 已知三棱锥 中,若
中,若 ,
, ,
, 两两互相垂直,作
两两互相垂直,作 平面
平面 ,垂足为
,垂足为 ,则点
,则点 是
是 的( )
的( )
 中,若
中,若 ,
, ,
, 两两互相垂直,作
两两互相垂直,作 平面
平面 ,垂足为
,垂足为 ,则点
,则点 是
是 的( )
的( )| A.外心 | B.内心 | C.重心 | D.垂心 |
您最近一年使用:0次
解题方法
5 . 已知三棱柱 中,底面
中,底面 是边长为2的正三角形,
是边长为2的正三角形, 为
为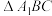 的重心,
的重心,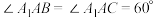
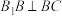 ;
;
(2)已知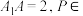 平面
平面 ,且
,且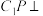 平面
平面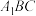 .求证:
.求证: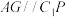 .
.
 中,底面
中,底面 是边长为2的正三角形,
是边长为2的正三角形, 为
为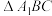 的重心,
的重心,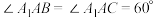

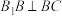 ;
;(2)已知
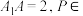 平面
平面 ,且
,且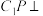 平面
平面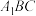 .求证:
.求证: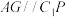 .
.
您最近一年使用:0次
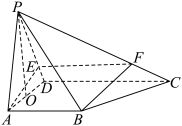
6 . 已知四棱锥 的底面
的底面 是直角梯形,
是直角梯形,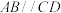 ,
,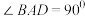 ,且
,且 平面
平面 ,垂足
,垂足 在线段
在线段 (不含端点)上,点
(不含端点)上,点 在棱
在棱 上,
上, ,平面
,平面 与棱
与棱 交于点
交于点 .
. ;
;
(2)若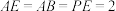 ,
, ;
;
①求四棱锥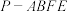 的体积;
的体积;
②求二面角 的余弦值.
的余弦值.
 的底面
的底面 是直角梯形,
是直角梯形,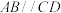 ,
,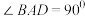 ,且
,且 平面
平面 ,垂足
,垂足 在线段
在线段 (不含端点)上,点
(不含端点)上,点 在棱
在棱 上,
上, ,平面
,平面 与棱
与棱 交于点
交于点 .
.
 ;
;(2)若
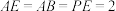 ,
, ;
;①求四棱锥
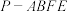 的体积;
的体积;②求二面角
 的余弦值.
的余弦值.
您最近一年使用:0次
名校
解题方法
7 . 如图, 和
和 都垂直于平面
都垂直于平面 ,且
,且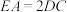 ,
, 是
是 的中点.
的中点.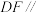 平面
平面 ;
;
(2)若 是正三角形,且
是正三角形,且 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 和
和 都垂直于平面
都垂直于平面 ,且
,且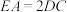 ,
, 是
是 的中点.
的中点.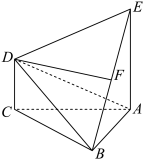
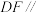 平面
平面 ;
;(2)若
 是正三角形,且
是正三角形,且 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-06-28更新
|
276次组卷
|
2卷引用:浙江省温州市十校联合体2023-2024学年高一下学期期中联考数学试题
8 . 设m,n是两条不同的直线, ,
, ,
, 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若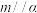 ,
, ,则
,则
②若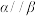 ,
,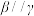 ,
, 则
则
③若 ,
, ,则
,则
④若 ,
,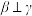 ,则
,则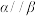
其中正确命题的序号是( )
 ,
, ,
, 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:①若
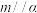 ,
, ,则
,则
②若
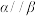 ,
,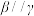 ,
, 则
则
③若
 ,
, ,则
,则
④若
 ,
,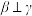 ,则
,则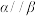
其中正确命题的序号是( )
| A.①② | B.②③ | C.③④ | D.①④ |
您最近一年使用:0次
9 . 如图, 是圆的直径,
是圆的直径, 垂直圆所在的平面,
垂直圆所在的平面, 是圆上的动点且不与
是圆上的动点且不与 重合.下列判断中正确的有( )
重合.下列判断中正确的有( )
 是圆的直径,
是圆的直径, 垂直圆所在的平面,
垂直圆所在的平面, 是圆上的动点且不与
是圆上的动点且不与 重合.下列判断中正确的有( )
重合.下列判断中正确的有( )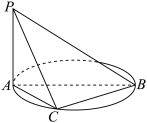
| A.三棱锥四个侧面都是直角三角形 |
B.平面 平面 平面 |
C.在圆上始终存在一点 ,使得 ,使得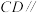 平面 平面 |
D.若 , ,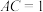 , , ,则二面角 ,则二面角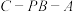 的正切值为 的正切值为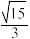 |
您最近一年使用:0次
解题方法
10 . 如图,在三棱锥 中,
中,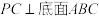 ,
, ,
, 、
、 分别是
分别是 ,
, 的中点.
的中点.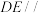 平面
平面 ;
;
(2)求证: ;
;
(3)若 ,求三棱锥
,求三棱锥 表面积.
表面积.
 中,
中, ,
, ,
, 、
、 分别是
分别是 ,
, 的中点.
的中点.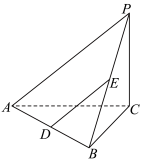
 平面
平面 ;
;(2)求证:
 ;
;(3)若
 ,求三棱锥
,求三棱锥 表面积.
表面积.
您最近一年使用:0次



